一种基于RBM的滚动轴承退化指标构建方法

程道来，魏婷婷，潘玉娜，马向华

(1.上海应用技术大学 城市建设与安全工程学院，上海 201418；2.上海应用技术大学 机械工程学院，上海 201418；3.上海应用技术大学 轨道交通学院，上海 201418；4.上海应用技术大学 电气与电子工程学院，上海 201418)

滚动轴承作为旋转机械中常用部件之一，对其振动信号进行监测与报警，可以有效降低机械维护成本，避免造成意外损失[1]。对滚动轴承做出正确的状态监测是对其做出预诊断和维修决策的基础[2]。但由于轴承工作环境的影响，其振动信号往往是非线性和非平稳的，且存在各种噪声的干扰等[3]，使得利用轴承振动信号对其进行精确的性能退化评估并不简单。而性能退化评估中的关键之处则在于退化指标构建的质量[4]。

近年来，为了精确评价轴承性能退化过程，出现了大量的退化指标构建技术。退化指标的构建可分为物理退化指标和虚拟退化指标两大类[5]。物理退化指标与设备失效物理特性有关，一般采用统计方法或信号处理方法从监测信号中提取[6]，常见的有时、频域统计指标[7-8]。复杂度指标如：张龙等提出包络谱谱峰因子(crest of envelope spectrum，EC)作为复平移Morlet小波滤波器的中心频率和带宽参数选择的依据，再将经过滤波信号的RMS值与EC值的乘积作为轴承故障程度评估指标；Liu等[9]利用改进的集成经验模态分解(ensemble empirical mode decomposition，EEMD)构建健康指标，对滚动轴承性能退化过程做出了准确评估。但单一指标会存有只能在特定的故障和操作条件下才能获得较好的评估结果的问题。

对于虚拟退化指标，它是通过融合多个物理退化指标或多传感器信号来构建的，通常这种方式构建的退化指标没有明显的物理意义，只是虚拟地描述了轴承的退化趋势。潘玉娜等[10]对轴承振动信号进行小波包分解，以其节点能量作为退化特征，选择支持向量数据描述(support vector data description，SVDD)做评估模型完成轴承退化指标的构建。Zhang等[11]提取出退化特征后，使用基于马氏距离(Mahalanobis distance，MD)的评估方法融合多个特征后描述轴承健康状态。Wang等[12]利用希尔伯特变换与鲁棒局部均值分解相结合的原始信号去噪和时频域特征提取，再使用隐马尔科夫(Hidden Markov model，HMM)模型建立轴承的退化指标。Rai等[13]提取出正常状态下轴承振动信号的时域和频域特征用来训练自组织映射网络(self-organizing map，SOM)，并定义测试数据输入SOM中得到的最小量化误差作为健康指标。周建民等[14]采用时域方法和集成经验模态分解的能量熵提取轴承特征，经过挑选后得到最终的退化特征，而定义轴承性能退化指标是用三种不同故障程度的轴承数据训练(support vector machine，SVM)模型，将轴承全寿命周期数据输入模型后，得到轴承性能退化曲线。但以上方法退化特征主要基于人工提取，构建的退化指标高度依赖先验知识，且有的方法中构建退化指标的模型需要故障数据，忽略了设备实际运行中难以获取故障状态下数据的问题。

深度学习在滚动轴承故障分类诊断上应用颇为广泛[15-18]，其强大的自学习能力摆脱了在信号处理中对人工经验的依赖，基于监督学习的轴承故障分类诊断需要标记不同类型的故障数据训练模型，而轴承的性能退化过程是循序渐进的变化，将其简单的归为故障分类诊断并不合适，有学者尝试将无监督深度学习方法应用在轴承退化指标构建上。如Pan等[19]利用正常状态下的轴承数据建立深度自编码模型(deep auto-encoder，DAE)，然后通过对输入数据进行编码和解码，利用重构数据与输入数据之间的均方根误差来评价轴承的健康状态。受限玻尔兹曼机(restricted Boltzmann machine，RBM)作为无监督学习的模型之一，能够通过调整模型的参数使得模型的概率分布尽可能地符合训练数据的真实分布，同时也能达到降维和特征提取的作用。

基于以上分析，本文提出一种基于RBM的退化指标构建方法。该方法以滚动轴承正常状态下归一化的幅值谱作为RBM模型的训练样本，模型训练完成后，将其输出作为退化指标构建的基础。通过不同情境下的滚动轴承全寿命周期试验数据验证了该方法可以很好的揭示轴承退化规律。

1 理论介绍

1.1 幅值谱

幅值谱获得方式即对采样所得的时域信号进行快速傅里叶变换(fast Fourier transform，FFT)，求得关于该时域信号的频率构成信息，其数学表达式为

(1)

式中，x(t)为时域信号。对于时域离散信号有

(2)

1.2 受限玻尔兹曼机

受限玻尔兹曼机是由多伦多大学的Salakhutdinov等[20]提出的，其作为一种特殊的马尔可夫随机场，可以在观测数据和隐藏特征之间建立联合分布。RBM主要由用于输入数据的可见层v和提取特征的隐含层h组成，其结构如图1所示。

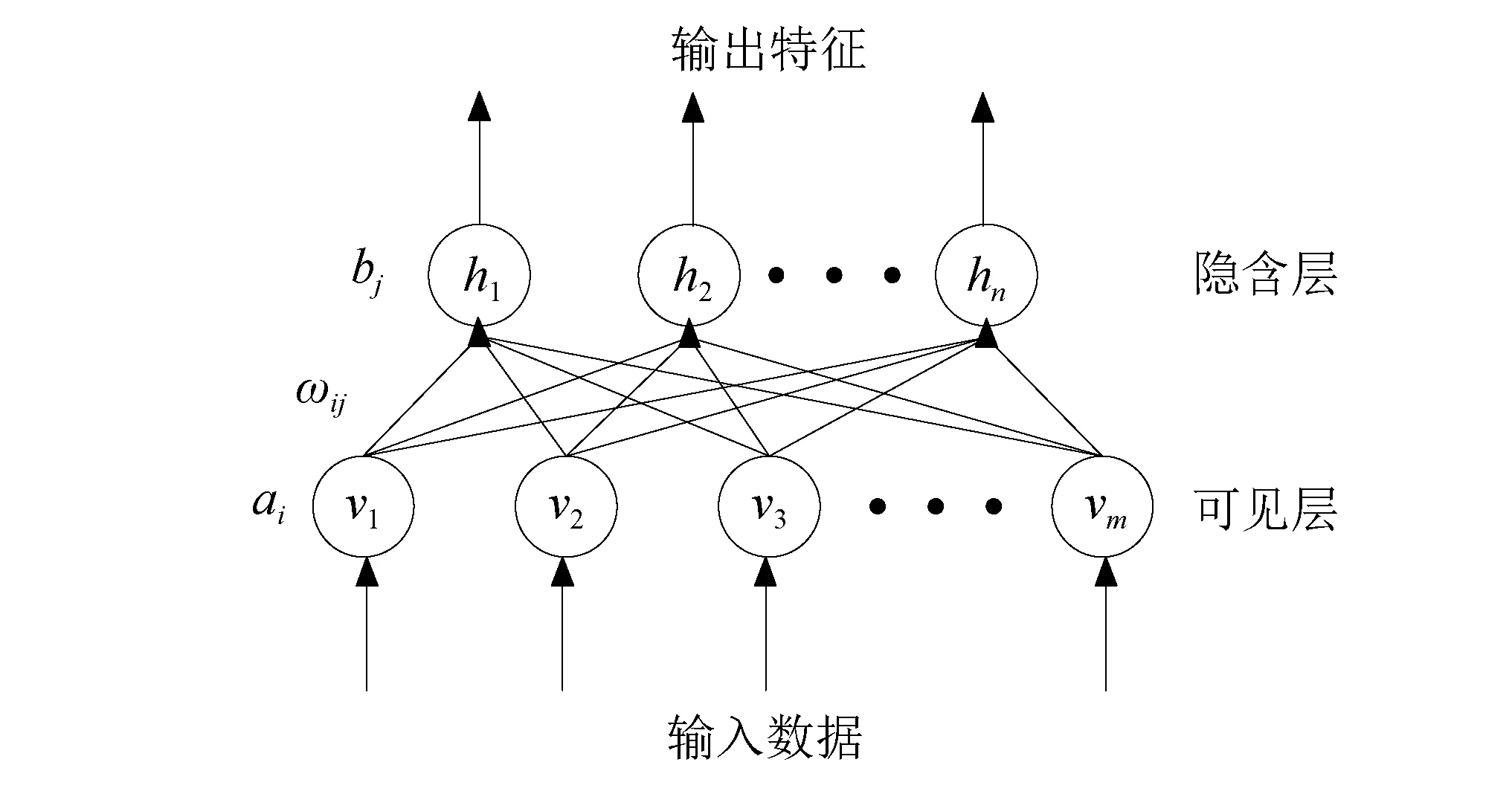
图1 受限玻尔兹曼机结构简图Fig.1 Structure schematic of RBM

可视层v和隐含层h中分别包含几个独立不相互连接的神经元，但层与层之间是完全连接的。受限玻尔兹曼机是一个基于能量的模型，假设图1所示的RBM中，可视层v有m个可见单元，隐含层h有n个隐含单元，ai和bj分别表示可视层vi和隐含层hj的偏置项，ωij是可视化层第i个单元和隐含层中第j个单元之间的连接权重，对于上述网络，给定一组状态(v,h)，则可自定义其能量函数

(3)

RBM里用来描述训练样本的分布，引入了属于热力学统计物理的相关概念即正则分布，是物理学家用来描述一个不知所处状态的概率的函数[21]

(4)

式中：Pθ为系统处于状态的概率；Eθ系统处于状态θ时的能量；Zθ为归一化因子。处于该状态的能量越小，则属于该状态分布的概率越大，系统也就越稳定。

将式(3)代入式(4)可得状态(v,h)的联合概率分布为

(5)

对应其联合概率密度分布的边缘分布即观测数据v的概率分布表达式为

(6)

通过训练得到模型参数ωij，ai，bj后，由于RBM层间有连接，层内无连接，且层内单元的激活值为零一分布的特殊结构，可以通过计算可见层和隐含层中单元激活的条件概率分布确定Pθ(v)[22]，其中隐含层h中第s个单元节点激活的概率为

(7)

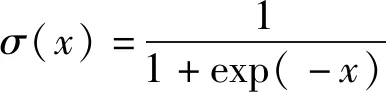
推导过程如下：

为方便推导过程，首先记h-s表示在h中挖掉分量hs后得到的向量；

h-s=(h1,h2,…,hs-1,hs+1,…,hn)T

(8)

并记

(9)

和

(10)

则有

Eθ(v,h)=-Q(v,h-s)-Os(v)

(11)

对Pθ(hs=1|v)的推导有

Pθ(hs=1|v)=Pθ(hs=1|h-s,v)=

(12)

当给定隐含层单元的状态时，由于各可见单元的激活状态之间是条件独立的，则第s个可见单元节点的激活概率为

(13)

训练数据输入到RBM中，相关参数ωij，ai，bj按照一定的更新准则改变，该准则是由Hinton等[23]提出的基于Gibbs采样的k步对比散度(contrastive divergence，CD-k)算法，该算法已成为训练RBM的标准算法，更新准则为

(14)

ai=ai+η[P(hj=1|v)-P(hj=1|vk)]

(15)

(16)

式中：k为采样步数，默认取值为1；η为学习率。

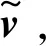
(17)

式中：d为训练样本输入时的批次大小，m为训练样本的长度即图1中可见层单元数；err为平均每个样本下每个点的重构误差。向训练完成的RBM模型输入测试样本hc，则其输出为隐含层节点为1的激活概率，可认为是测试数据属于训练数据分布的概率P，由式(7)可得

(18)

又因单元节点为零一分布，则可认为其隐含层节点为0的概率是测试数据不属于训练数据分布的概率，大小即为1-P。

2 退化指标的构建

基于RBM的理论特点，本文提出了一种基于RBM的滚动轴承性能退化指标构建方法，其特点为隐含层单元数设置为一个，基于该方法的滚动轴承性能退化评估模型如图2所示。其具体步骤为：

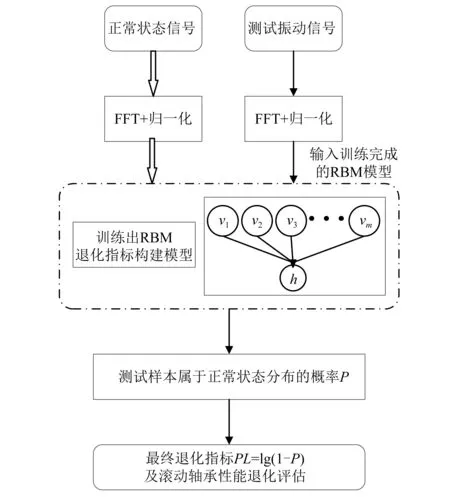
图2 基于RBM的退化指标构建方法流程Fig.2 Flow chart of degradation index construction method based on RBM

步骤1收集滚动轴承正常状态下的振动信号，经过FFT处理后再进行归一化；

步骤2将步骤1处理后的滚动轴承正常状态下的数据作为训练样本，建立RBM退化指标构建模型；

步骤3对于测试的滚动轴承全寿命周期振动信号，将经过步骤1处理得到的样本，再依次经过步骤2中已经训练完成的RBM退化指标构建模型，可求得测试样本属于轴承正常状态分布的概率P；

步骤4以步骤3中得到的概率P为基础，计算得出最终的退化指标PL，计算公式为

PL=lg(1-P)

(19)

其中PL的意义即对测试样本不属于轴承正常状态分布的概率做以十为底的对数计算，以此增加退化指标对轴承整个退化过程区分的敏感性。

3 试验验证

3.1 试验数据介绍

采用了文献[24]中试验所得的滚动轴承全寿命周期试验数据，其中轴承型号为6307，转速为3 000 r/min，径向载荷1.113 kg，采样频率为25.6 kHz，采用加速度传感器每隔1 min采集一组长度为20 480的数据，数据采集从轴承正常状态一直持续到寿命结束，共采集了1 062组数据，最终失效形式均为内圈严重点蚀，将此组数据记为B1。

另外，为了验证本文所提方法应用在不同情境下的滚动轴承也能实现较好的退化评估，同时选择了源于美国辛辛那提大学公布的滚动轴承振动测试的全寿命周期数据[25]进行试验验证，该试验台中有4个施加了27 00 kg径向载荷的型号为ZA-2115的轴承，在运行了163 h后一轴承外圈出现严重剥落故障直至失效，轴承振动信号每隔10 min采集一次，采样频率20 kHz，共采集到984组样本，每个样本包含20 480个数据点，将此组数据记为B2。

3.2 基于RBM的退化指标评估结果

对B1和B2两组滚动轴承数据做基于RBM的退化指标PL的构建。其中，RBM可见层和隐含层神经单元个数分别设置为1 024和1；训练批次设置为100；学习率设置为0.01；训练样本两组均选择了前300个正常样本。训练时的两组模型重构误差随迭代次数变化如图3所示，随着迭代次数的增加逐渐降低并且收敛，在误差趋于稳定时即该模型训练完成。为增加训练速度，训练时迭代次数设置为50。

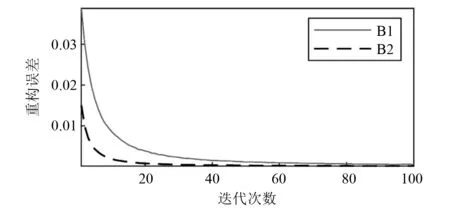
图3 重构误差随迭代次数变化Fig.3 The reconstruction error varies with the number of iterations

首先对B1进行分析，其全寿命周期退化指标PL如图4所示。0～513 min期间PL基本保持稳定，说明此阶段的滚动轴承处于正常工作状态；从513 min开始PL值出现小幅上升，之后保持稳定，可认为此时轴承进入了早期微弱故障状态；在978～1 039 min期间的样本PL值断崖式上升且保持稳定，说明此阶段轴承属于故障加剧状态；1 039 min后的PL值波动较大且变化毫无规律，反映出轴承此刻进入失效状态。

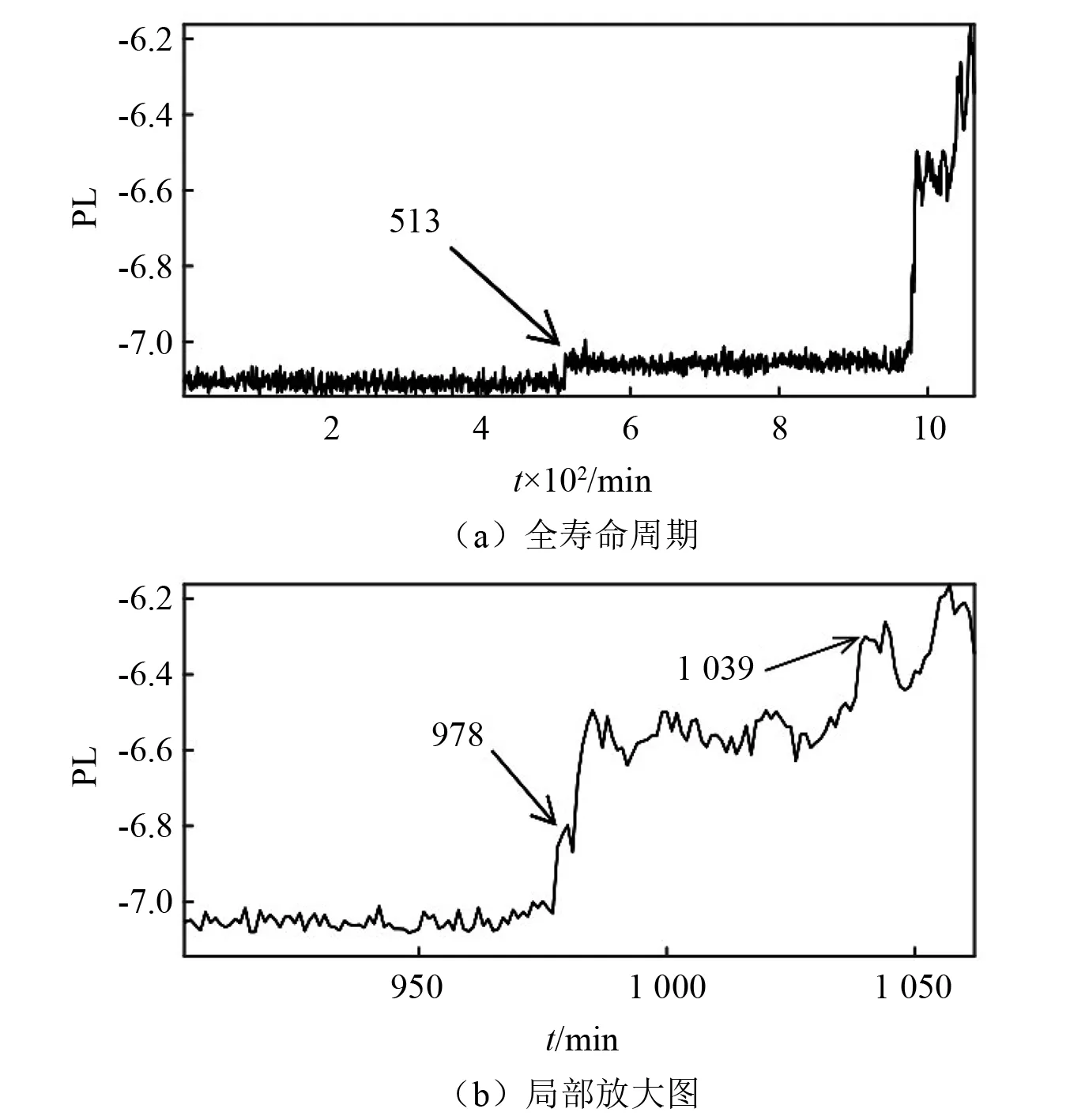
图4 B1全寿命周期PL退化指标Fig.4 Full life cycle PL degradation index of B1

然后对B2进行分析，其全寿命周期下的退化指标PL如图5所示。在滚动轴承运行的0～5 340 min期间，样本的PL值较为稳定，说明其运行属于正常状态；在5 340～7 030 min期间的PL值逐渐上升，可认为轴承从5 340 min出开始出现早期微弱故障，且随着时间的变化，早期微弱故障的特征越明显；在运行的7 030 min～9 710 min期间，样本的PL值再次上升并伴随小幅波动，说明此时段的轴承运行属于故障加剧状态；从9 710 min开始的PL值波动较大且毫无规律，说明该期间的轴承已经失效。

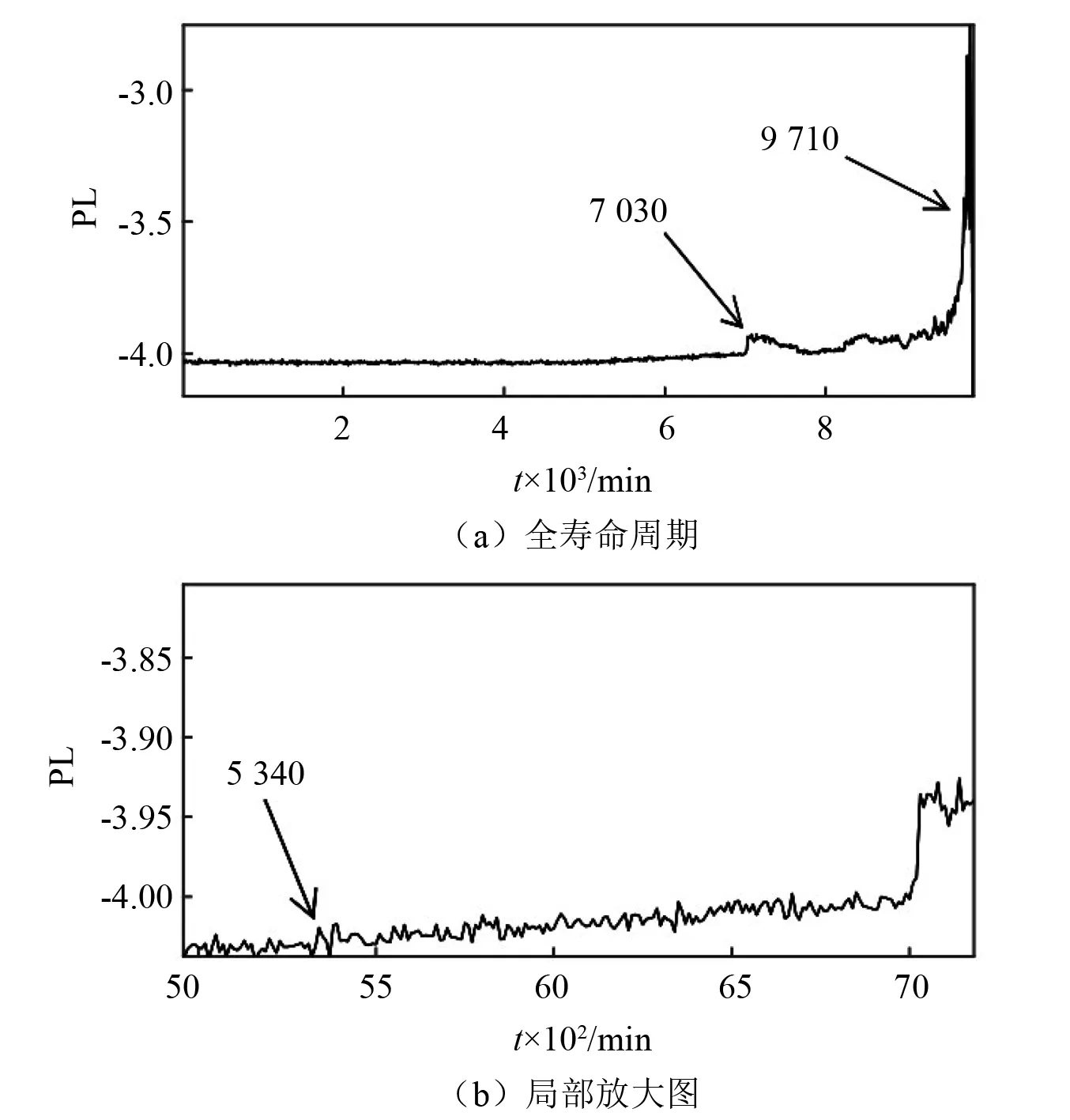
图5 B2全寿命周期PL退化指标Fig.5 Full life cycle PL degradation index of B2

3.3 结果对比分析

本文所提指标对B1退化评估的变化趋势与文献[26]中的相一致，验证了本文方法的有效性。对B2的退化评估分别与文献[27]和文献[28]所提方法做出的结果相比，其中两篇文献分别构建的是物理退化指标和虚拟退化指标，且主要是针对检测轴承早期微弱故障提出的，对比结果为本文所提方法与上述两篇文献中发现早期微弱故障出现的时刻相同，验证了本文方法具有一定的早期微弱故障检测能力。另外，张龙等研究中自适应最优频带选择的过程中多处依赖专家经验知识，如：能得到比较满意的中心频率时寻优取值点的确定，带宽的确定；王斐等中提到其经过大量分析研究才选定VMD奇异值，均方根值，样本熵值作为SVDD模型的输入，进而得到较好的轴承性能退化评估，而本文所提方法中的RBM可自动提取出退化指标，无需依赖专家经验知识以及人工在构建退化指标花费大量时间选择退化特征。

为了进一步验证本文所提方法的优越性，使用同是属于无监督学习的深度自编码网络模型对这两组数据做出性能退化评估，并与本文方法做出的结果进行对比分析。将基于DAE模型提取出的退化指标记为DAE-DI(DAE-degradation index)，对B1组滚动轴承数据做基于DAE的性能退化评估，其全寿命周期的DAE-DI值变化如图6所示，DAE-DI对B1组数据的性能退化评估单调性较差，无法明确检测出早期微弱故障出现的时刻，但其对轴承后期的退化过程的评估还是比较准确的。对B2组数据做基于DAE的性能退化评估，其全寿命周期的DAE-DI值变化如图7所示，DAE-DI对B2组数据的性能退化评估具有一定的单调性，能够表现出滚动轴承的性能退化的大致趋势，但所得曲线过于粗糙，淹没了早期微弱故障刚出现时的特征，同样无法准确检测出早期微弱故障出现的时刻。

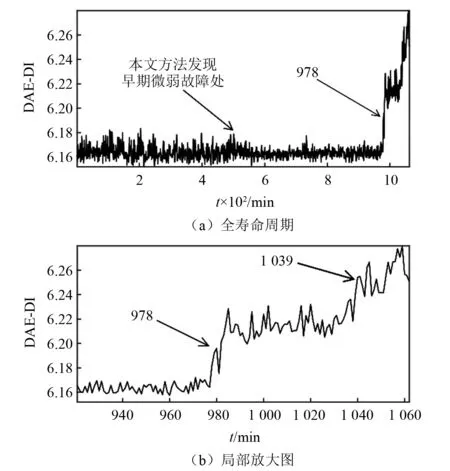
图6 基于深度自编码的B1全寿命周期退化指标Fig.6 Full life cycle degradation index of B1 based on DAE

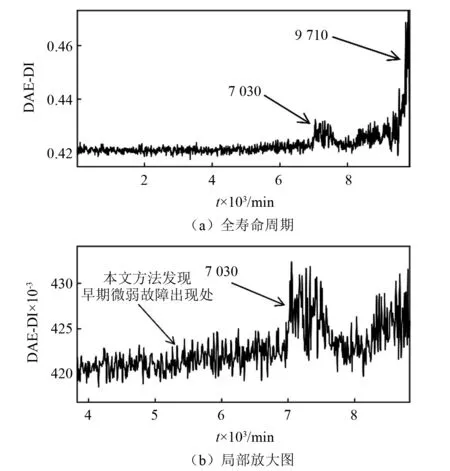
图7 基于深度自编码的B2全寿命周期退化指标Fig.7 Full life cycle degradation index of B2 based on DAE

由上述分析可知，基于RBM构建的退化指标应用在不同情境下的滚动轴承都能够清晰反映出其性能退化的过程，该指标对早期微弱故障也具有一定的敏感性，并且指标构建过程避免了人工先验知识的参与；另外，相较于同是属于无监督学习的DAE网络模型做出的轴承性能退化评估结果，基于RBM构建的退化指标表现更好。

4 结 论

(1)介绍RBM相关理论的同时说明了RBM隐含层单元节点输出的意义，并提出了一种基于RBM的滚动轴承退化指标构建方法，将其隐含层输出作为退化指标构建的基础。

(2)与最近相关文献相比，基于RBM构建退化指标面对不同情境下的滚动轴承都能够有效评估出其性能退化过程，准确检测出滚动轴承早期微弱故障的出现，摆脱了对人工经验的依赖，且在一定程度上节省了时间与精力。

(3)与同是属于无监督学习的DAE构建的退化指标相比，基于RBM构建的退化指标表现更佳。

(4)用正常状态下的数据即可实现该模型的构建，克服实际轴承设备运行中故障样本较难获取的问题，对于轴承设备性能监测具有很好的指导意义。