数传天线机电耦合建模及微振动特性仿真与试验研究

郑照明月，程 伟，王光远，李 名

(1.北京航空航天大学 航空科学与工程学院，北京 100191；2.四川航天系统工程研究所，成都 610100;3.中国空间技术研究院,北京 100094)

为了继续提升高分辨率遥感卫星的成像质量，遥感卫星的稳定度要求随之不断提升[1]。但卫星上存在着控制力矩陀螺，动量轮，太阳翼驱动机构，数传天线等活动部件[2-6]。卫星在轨运行时，活动部件会产生微振动。微振动不仅影响相机等有效载荷的分辨率和指向精度，而且还可能影响卫星姿态控制[7]。其中，星载数传天线在航天器数据中继和星间链路等任务中扮演着重要角色，但也是低频段微振动的主要扰振源[8-10]。

混合式两相步进电机由于其结构简单、定位精度高、易于开环控制电路等优点，在航天器活动部件低速转动上应用广泛[11-12]。目前，细分驱动(subdivision driving,SDD)被广泛使用，它通过将电流变化细分为多个微电脉冲来提高电机的分辨率[13]和操作的平稳性[14]。星载数传天线由两个垂直布置的步进电机驱动反射器转动[15]。反射器为较大尺寸的柔性结构，通过驱动机构与支撑臂连接。为了提高数传天线的指向范围，避免反射器与卫星本体出现干涉，双轴数传天线的支撑臂被设计为较长的尺寸，且具备一定的柔性。在天线工作时，步进电机的电脉冲信号和减速机构的啮合齿谐波传动都会产生微扰动[16-17]。这种微扰动可能引起柔性负载-反射器、柔性边界-支撑臂产生结构振动，并反作用于步进电机。进而既影响星上有效载荷的性能指标，又会影响数传天线本身的指向精度。所以，数传天线的微振动现象可以归纳为在柔性边界上步进电机驱动柔性负载的耦合振动问题，而这种问题的建模和分析比较复杂。

多数研究者以数传天线的指向精度为设计目标，从步进电机和控制方法的角度建模。刘辉等[18]从指向算法、指向执行、地面站指向、大气传输等方面分析了数传天线指向精度的影响因素。周勇等[19]考虑了谐波齿轮的非线性和驱动电路的动态特性，建立了数传跟踪天线驱动机构模型。这类思路虽能有效分析数传天线的指向精度，但却无法预测数传天线产生微振动的力矩大小。部分研究者从柔性结构角度建立了数传天线的动力学模型。宋建虎[20]通过有限元法建立了数传天线的动力学模型，计算分析了振动特性。Cao等[21]通过采用加载模态综合-混合坐标法建立了数传天线的柔性耦合动力学方程。他们的研究未考虑步进电机与柔性结构的耦合作用，不能准确解释数传天线的微振动现象。

在步进电机与结构耦合振动的研究中，Yang等[22]通过试验和仿真验证了步进电机存在电磁刚度。刘希刚[23]根据步进电机原理，将负载简化为刚性，建立了数传天线的微振动的一般解析模型和简化模型。Chen等[24]通过简化和线性化步进电机的电磁转矩建立了步进电机的振动方程，并用两自由度柔性系统进行了仿真分析。Sattar等[25]根据拉格朗日能量法建立了步进电机与刚性载荷运动学和微振动耦合的动力学模型。他们在研究中未考虑负载柔性和边界柔性的影响，或对负载柔性和边界柔性进行一定程度的简化。也有研究者通过试验研究了数传天线的微振动现象，但未深入讨论其产生原因和耦合机理。Wu等综合考虑了步进电机和天线结构模态，通过试验给出了一种半经验半解析的数传天线微振动模型。Oh等使用KISTLER公司生产的测力台测试了一种数传天线的微振动，并设计了一种可以抑制其微振动的伪弹性SMA网垫。但他们均未揭示步进电机和天线结构的耦合关系。因此，需通过数学建模研究在柔性边界上步进电机驱动柔性负载的耦合振动问题，并通过试验验证和分析数传天线微振动产生的机理和影响因素。

本文研究了在柔性边界上步进电机驱动柔性负载的动力学模型。通过线性化方法简化了步进电机的动力学方程。采用动态子结构方法建立了在柔性边界上步进电机驱动柔性负载的动力学模型，并给出了数传天线微振动的解析表达式。通过坐标变化法分析了系统振动的耦合关系。最后，通过仿真和试验验证了方法的有效性。

1 双轴数传天线机电耦合模型

1.1 电流细分化的步进电机动力学方程的简化

两相混合式步进电机的驱动模型为

(1)

式中：Φ为磁链矢量；I为电流矢量;L为电感矩阵。电感矩阵为对称矩阵，忽略周期性磁导函数的高阶谐波分量，电感矩阵可表示为

式中，z为转子齿数。为了使步进电机运行过程具备较好的平稳性，通常将步进电机的驱动电流进行阶梯化细分，因此电流矢量I可表示为

(3)

式中：IA和IB分别为A,B两相绕组电流;If为永磁体的等效励磁电流；Im为两相绕组电流细分后的幅值;γ为电流细分后的电步距角;i为运行步数。

两相混合式步进电机的动力学模型为

(4)

式中：θ为转子的转角；J0和C0为电机转子的转动惯量和电机内部的黏性阻尼系数；Te和Tl为电磁转矩和负载转矩。由式(1)～式(3)，电磁转矩Te可化为

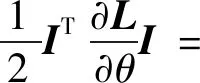
Km[IBcos(zθ)-IAsin(zθ)]-Kdcos(4zθ)=

(5)

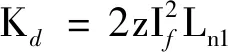
(6)

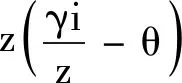
(7)

所以，电流细分化的步进电机的动力学方程可化为

(8)

式中：K0=KmImz为步进电机的等效电磁刚度;Tex=KmImγi为电磁转矩中的阶梯激励，该分量与转子角位移无关。根据上式可知，电流细分化的步进电机可等效为电磁弹簧-阻尼系统，为进一步分析步进电机和数传天线柔性负载和柔性支撑臂的耦合振动提供基础。

1.2 柔性结构动力学模型降阶

双轴数传天线由支撑臂、X轴步进电机、Y轴步进电机和反射器组成，其中支撑臂和反射器为柔性结构。图1给出了双轴数传天线的结构示意图。采用有限元方法对柔性结构建模时，结构自由度高，迭代计算量大，效率低。故选用动态子结构方法，对柔性结构的动力学模型进行缩聚，将高自由度的物理坐标转化成低自由度的模态坐标，从而提高了计算效率。数传天线的微振动主要集中于低频段，忽略高阶模态影响对计算精度影响不大。

图1 双轴数传天线结构示意图Fig.1 Structure diagram of data transmission antenna

图2给出了双轴数传天线的坐标系，XYZ定义为惯性坐标系，x0y0z0为原点位于C点的固定坐标系，xayaza为中间坐标系，xbybzb为反射器坐标系。定义α为X轴电机转过的角位移，β为Y轴电机转过的角位移。首先，Y轴电机和反射器绕x0轴转动α至中间坐标系，然后，反射器绕ya轴转动β。坐标系的变换关系为

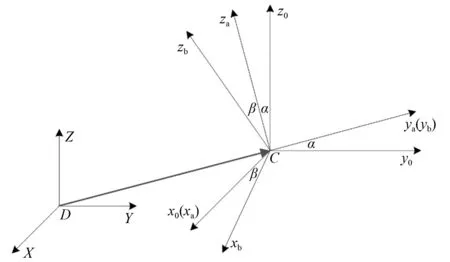
图2 双轴数传天线坐标系Fig.2 Coordinate system of data transmission antenna

(9)

式中：i0j0和k0为x0y0z0坐标系的单位向量;iaja和ka为中间坐标系xayaza的单位向量;ibjb和kb为xbybzb坐标系的单位向量;R(x0,α)和R(ya,β)为坐标转换矩阵。当天线反射器大角度转动后，天线构型和力学特征均会发生较大变化，在后续推导中，将通过引入坐标转换矩阵进行建模分析。

将数传天线分为4个子结构，子结构1～子结构4依次为反射器、Y轴步进电机、X轴步进电机和支撑臂。根据动态子结构方法，将子结构的自由度划分为内部自由度和界面自由度。子结构1在其局部坐标系的动力学方程为

(10)

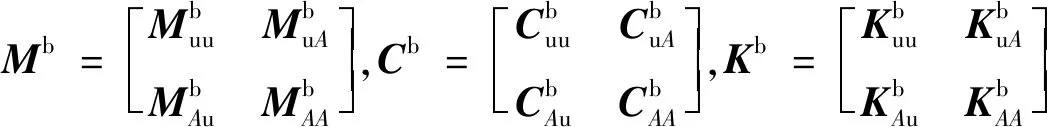
(11)

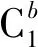
(12)

根据固定界面模态综合法，子结构的假设模态集由主模态和约束模态构成，子结构1的主模态和约束模态的求解方法为

(13)

(14)

式中，下标l代表子结构1保留的主模态阶数，将式(14)第一行展开可得

(15)

因此，子结构1在其局部坐标系的假设模态集为

(16)

子结构2和子结构3在自由界面下均为单自由度振动系统，仅存在一个扭转自由度，根据式(8)可将步进电机的动力学方程写为

(17)

(18)

式中：上标2和3分别为子结构2和子结构3，各物理量的含义为

M2=J0+Jβ,M3=J0+Jα,C2=C3=C0,

K2=K3=K0,F2=F3=Tex

(19)

根据式(13)～式(15)给出方法，可得子结构2和子结构3的假设模态集

φ2=φ3=1

(20)

子结构4同样为柔性结构，其动力学方程为

(21)

(22)

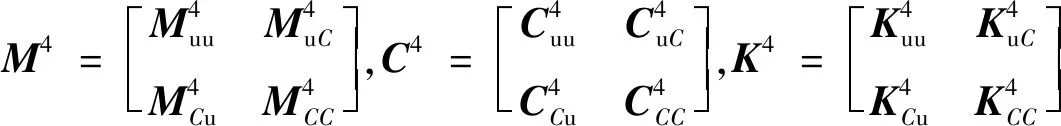
(23)

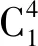
得到所有子结构的假设模态集后，可将系统的质量矩阵、阻尼矩阵、刚度矩阵、位移列向量、激励列向量和模态矩阵定义为

(25)

对应于模态矩阵φ的模态坐标Xp可写为

(26)

X=φXp

(27)

对系统的动力学方程进行第一次坐标变换，可将耦合系统自由度较高的物理坐标缩聚为自由度较低的混合坐标，即系统的动力学方程为

(28)

其中，

Mp=φTMφ,Cp=φTCφ,Kp=φTKφ,Fp=φTF

(29)

引入式(12)给出的坐标变换关系和界面位移协调条件

I4=(0 0 0 1 0 0)T,I5=(0 0 0 1 0 0)T(30)

式中，Rα和Rβ为子结构1在A点坐标的坐标转换矩阵，根据式(13)～式(16)的模态综合过程可知，子结构1的内部节点物理坐标在模态综合后，将通过模态坐标体现，模态综合前后是否对内部节点坐标变换不影响综合后的系统动力学方程，仅对界面节点A处的物理坐标进行坐标变换即可反映反射器在大角度转动后系统结构特征的变化，所以模型在反射器大角度转动后同样适用。同时，模态坐标Xp中各坐标并非完全独立，引入变换矩阵S，将Xp中非独立的坐标消去，得到耦合系统独立的模态坐标Xq

(31)

则耦合系统以自由度较低的独立模态坐标表示的动力学方程可写为

(32)

其中，

Mq=STMpS,Cq=STCpS,Kq=STKpS,Fq=STFp(33)

式(32)具备l+m+8阶自由度，各个坐标相互独立，并且XC，α和β具有明确的物理含义。便于结合控制方法，建立数传天线的机电耦合模型，同时较低的自由度保证迭代计算效率，各个坐标相互独立便于分析耦合关系。为了方便动力学模型与控制模型连接，将式(32)改写成状态空间形式，并用下标s表示结构

(34)

其中，

(35)

双轴数传天线的状态空间方程的阶数较低，提高了仿真效率，且状态空间方程的形式易与双轴电机的控制模型连接，进行联合仿真用以优化控制方法和控制参数。

2 微振动模型

双轴数传天线的步进电机启动后，驱动系统会给电机输入脉冲激励电流，使其行星齿轮在啮合过程中产生激振。电流脉冲引起振动的基频f0为

(36)

(37)

3 仿真与试验验证

3.1 Simulink仿真模型

首先，通过模态试验获取数传天线的低阶模态，表1给出了数传天线的模态频率和振型，结合模态试验结果建立数传天线的有限元模型。分别提取柔性结构反射器和支撑臂的质量矩阵和刚度矩阵，由于数传天线的微振动主要集中在低频段，子结构1和子结构4的仅保留前10阶模态进行模态综合，表1最后一列给出了模态综合后的系统频率。再根据第一章给出方法得到耦合系统动力学方程的状态空间形式，使用MATLAB的Simulink模块建立了数传天线的仿真仿真模型，如图3所示。表2给出了仿真过程中使用的参数，阻尼系数根据天线材料及试验结果共同确定。

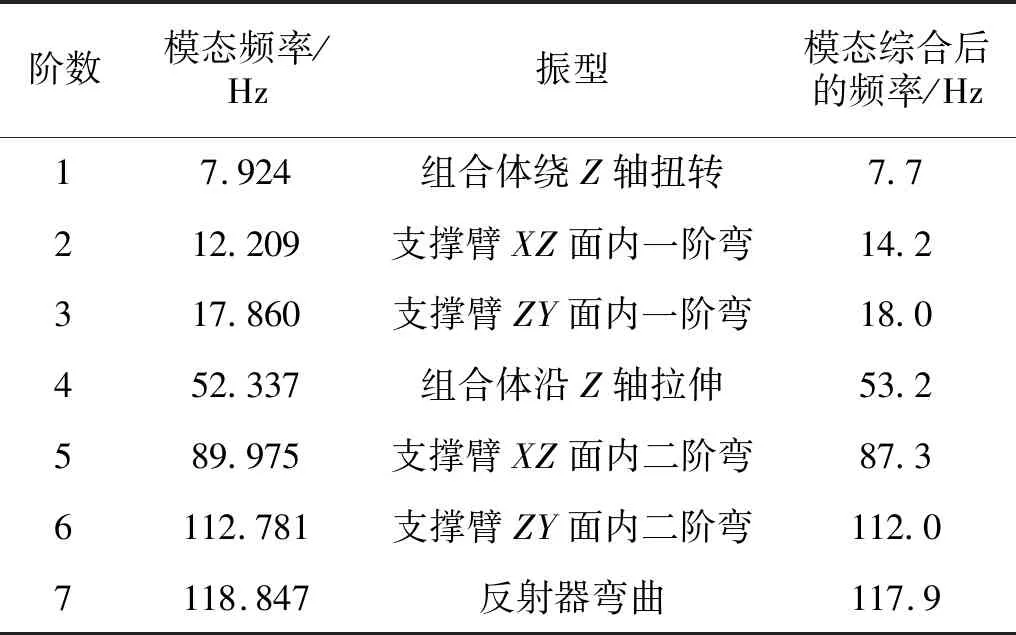
表1 数传天线模态Tab.1 Mode of data transmission antenna

图3 双轴数传天线仿真模型Fig.3 Simulation model of data transmission antenna

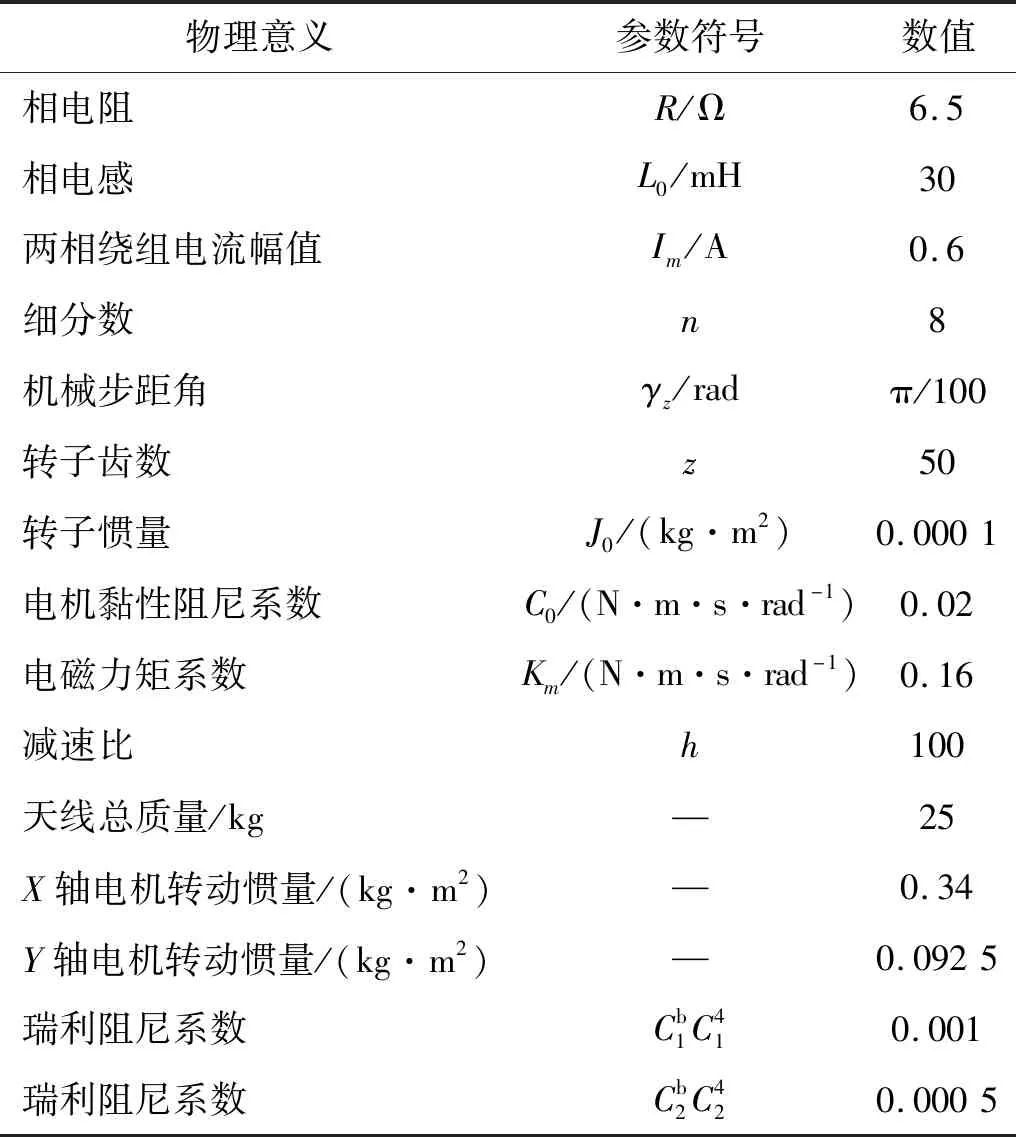
表2 仿真参数Tab.2 Simulation parameters

3.2 微振动试验

试验系统包含3个部分：待测设备、测试设备、零重力状态模拟设备，如图4所示。待测设备有数传天线和天线控制设备。测试设备有微振动测力台，单向力传感器，加速度传感器，力锤等。微振动测力台为一种高刚度的压电式测力台，由北京航空航天大学研制，其测试原理和方法由Chen等的研究给出，用于测量耦合系统产生微振动。单向力传感器在氦气球充气时，测量氦气球给吊绳的拉力。加速度传感器和力锤用于测试耦合系统的模态。

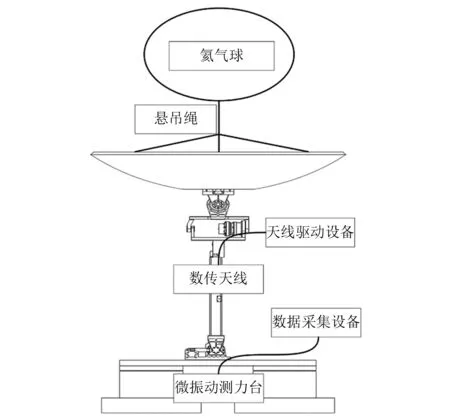
图4 微振动试验Fig.4 Micro vibration experiment

3.3 仿真与试验结果对比分析

图5给出了数传天线X轴电机和Y轴电机分别转动时的微振动的典型频域曲线，表3和表4给出了上述频域曲线峰值点的频率和幅值。X轴电机100.0 Hz,144.4 Hz和Y轴电机144.4 Hz 3个频点的微振动幅值较小(小于0.01 Nm)，试验时受环境噪声影响较大，导致试验与仿真的偏差较大，忽略上述3个频点微振动的结果。其他峰值处微振动的仿真和试验结果表明：频率一致，幅值误差不超过9.41%，所以双轴数传天线的微振动模型能准确预测耦合系统产生的微振动。

图5 微振动频域曲线对比Fig.5 Comparison of frequency domain curves of micro vibration

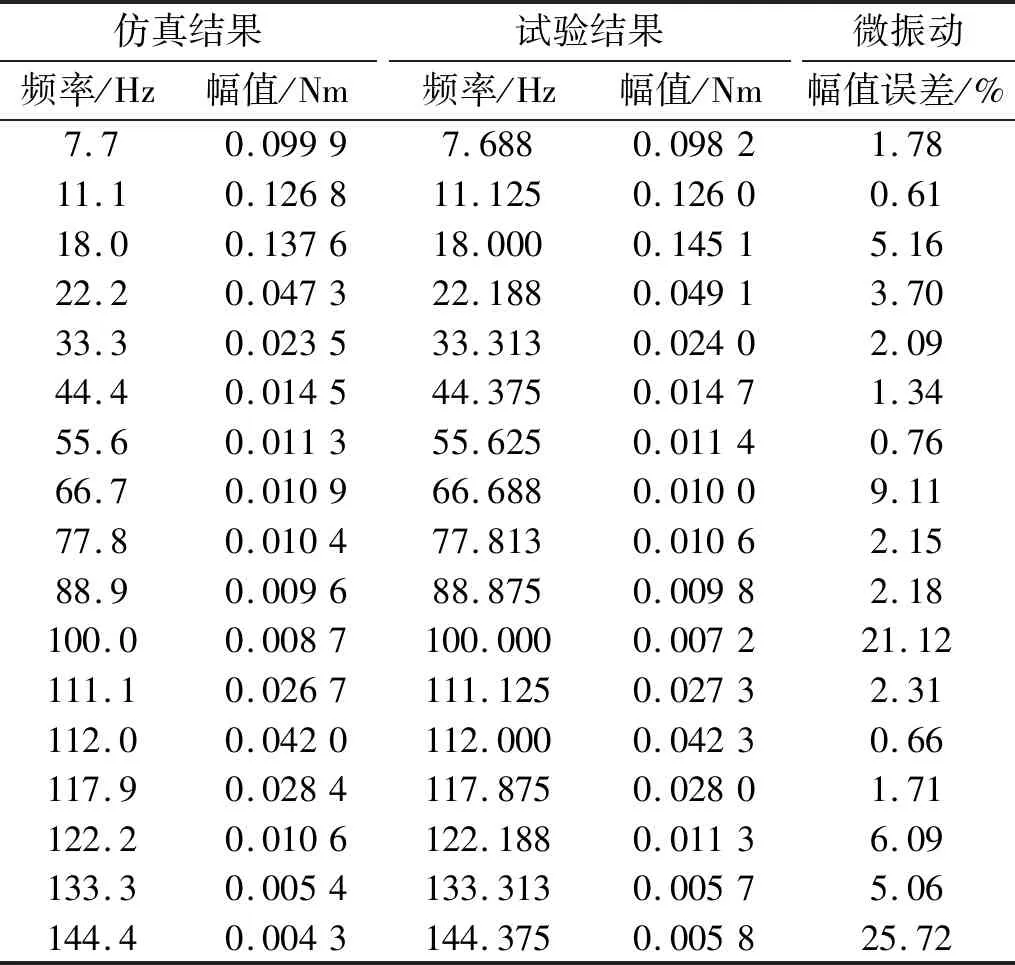
表3 X轴电机微振动频域峰值Tab.3 Micro vibration peak in frequency domain of X-axis motor

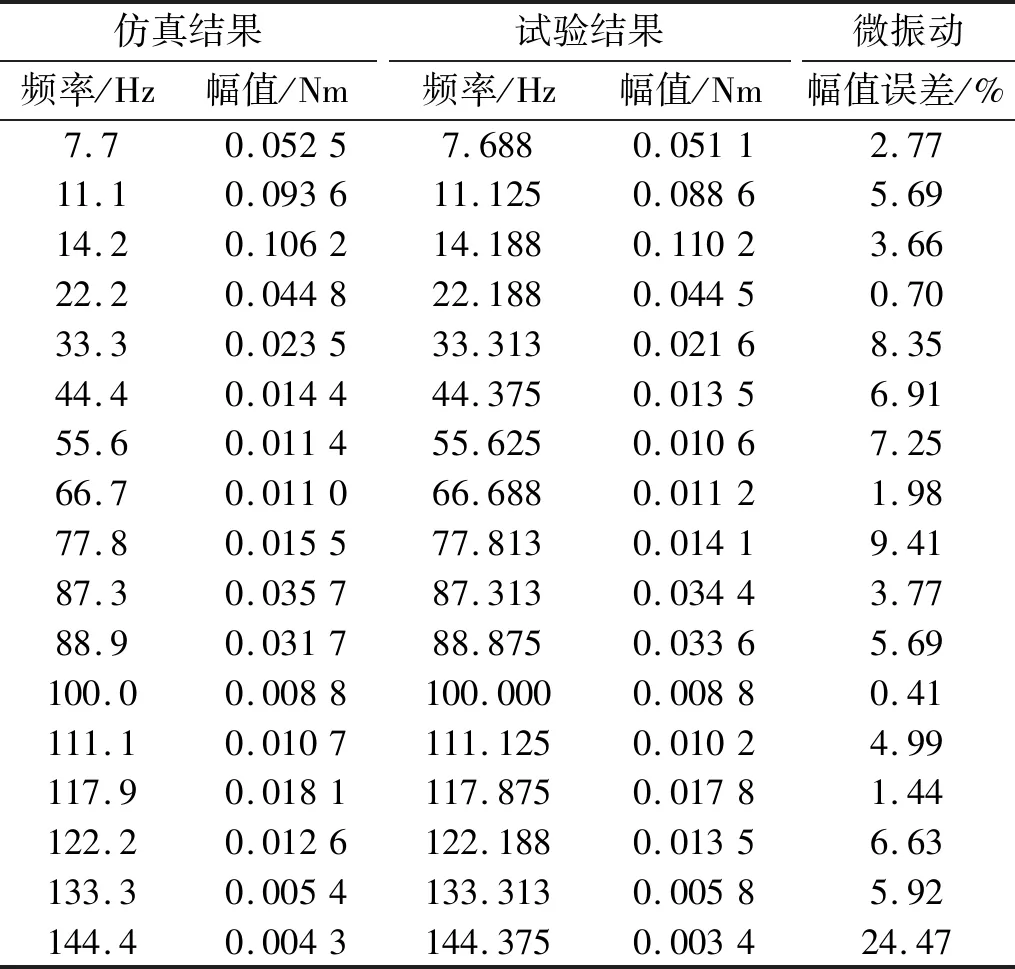
表4 Y轴电机微振动频域峰值Tab.4 Micro vibration peak in frequency domain of Y-axis motor

图6和图7给出了步进电机不同转速下的微振动结果。当X轴电机转动时，不同转速工况均出现了7.7 Hz,18.0 Hz,112.0 Hz和117.9 Hz的自然频率，分别对应结构第一、三、六、七阶模态频率7.9 Hz,17.8 Hz,112.7 Hz和118.8 Hz，这些模态振型均在X轴电机转动方向存在分量。当Y轴电机转动时，不同转速工况均出现了7.7 Hz,14.2 Hz,87.3 Hz和117.9 Hz的自然频率，分别对应结构的第一、二、五、七阶模态频率7.9 Hz,12.2 Hz,89.9 Hz和118.8 Hz，这些模态振型均在Y轴电机转动方向存在分量。以上现象表明，步进电机转动时，耦合结构在电机转动方向存在分量的模态频率上产生微振动。

图6 不同角速度的微振动仿真结果Fig.6 Simulation results of micro vibration with different angular velocity

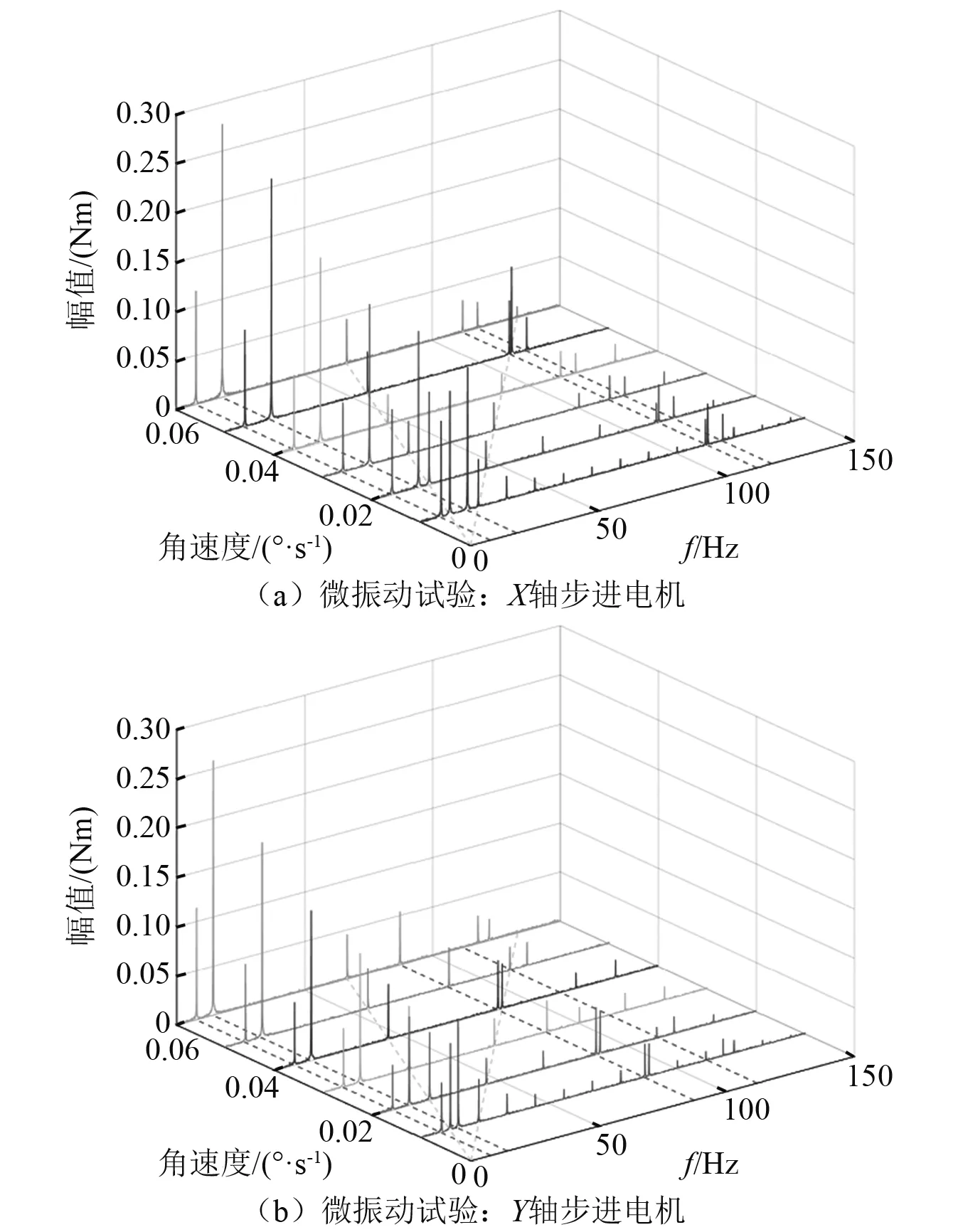
图7 不同角速度的微振动试验结果Fig.7 Experimental results of micro vibration at different angular velocities

同时，不同转速下在式(36)给出的电流脉冲基频和倍频出现了微振动峰值，如：转速0.01 °/s时，在11.1 Hz基频处和22.2 Hz,33.3 Hz等倍频处出现了微振动峰值。倍频处出现的微振动峰值是步进电机减速机构等传动装置在行星齿轮啮合过程中引起的。综上，数传天线的微振动成因主要有：①步进电机转动引起耦合结构在具有转动方向分量的模态频率附近发生结构振动；②脉冲激励电流产生的电磁激励；③行星齿轮在啮合过程中，产生了脉冲激励的倍频激励。

同时，当步进电机的转速较低时，耦合结构在低频段有较多的谐振频率。若脉冲激励电流产生的微振动的基频和倍频接近耦合结构的自然频率时，会出现微振动幅值共同放大的耦合现象。随着步进电机的转速提高，脉冲激励电流引起的微振动的基频和倍频随之提高，在低频段出现的谐振频率减少，与结构频率耦合的几率降低。然而随着转速的升高，耦合结构的低频微振动幅值随之提高。所以在天线设计阶段和使用过程中，应仔细考虑工作转速、励磁转矩、负载转矩、机械步距角等参数的影响，避免微振动与结构频率发生耦合。

4 结 论

分析了在柔性边界上步进电机驱动柔性负载的微振动现象。通过简化步进电机电磁力矩和动态子结构方法给出了一种面向控制系统的双轴数传天线的动力学方程，并给出了微振动的解析表达。通过仿真和试验验证了模型能准确预测耦合结构产生的微振动，结果表明微振动的主要成因为步进电机转动与柔性结构耦合、电磁脉冲激励、行星齿轮啮合等。