近平板圆柱涡激振动风洞试验研究

陈 聪，王汉封,2，邓国浩，姚小敏

(1.中南大学 土木工程学院，长沙 410075；2.中南大学 高速铁路建造技术国家工程实验室，长沙 410075)

在一些工程实践中，圆柱体或其他类似结构物被安装在平面边界附近，如海陆油气管道等。在以往众多的试验中，常将此类结构物简化为弹性支承的圆柱来模拟实际情况，但常见于孤立圆柱的研究[1-6]。而对于靠近壁面的圆柱来说，由于壁面的存在，圆柱的尾流涡脱以及响应特征将更为复杂[7-15]。

过去几十年里，对圆柱涡激振动的试验研究非常之多，主要从质量阻尼比(m*ζ)、自由度(DOF)和雷诺数(Re)等方面进行。其中，质量阻尼比是关注最多的一个参数，对圆柱的响应特性和尾流结构均有着极大的影响。就高质量阻尼比模型来说，随着雷诺数的增加，圆柱的位移表现出截然不同的两种响应状态，即初始分支和下分支；这两个分支间的转变并不是迅速发生的，而是存在一个迟滞过渡的过程。而对于低质量阻尼比模型的涡振试验来说，它有着与高质量阻尼比完全不一样的现象。试验结果表明，当模型质量阻尼比较低时，其最大响应振幅显著提升，且锁定区间的范围更宽；同时，响应曲线还出现振幅远高于初支与下支的一种新的分支，称之为上分支；其中，初支对应着2S的涡脱模式，而上支和下支对应着2P的涡脱模式。

相对于孤立圆柱来说，近壁面圆柱的涡振现象更加复杂。由水洞试验的研究结果可知，对于间隙比S/D≤0.3(其中S为圆柱下表面至壁面的间距，D为圆柱直径)，圆柱静止时的旋涡脱落受到壁面抑制，而当圆柱振动时，壁面反而促进尾流涡脱，致使其频率比大于1；此外，随着速度的变化，圆柱的最大振幅远高于间隙距离，甚至在极小间隙比(S/D=0.002)的情况下，圆柱仍可以产生大幅振动，但具体幅值的大小受到壁面反弹系数的影响。当0.3

本文采用了一套新型涡激振动试验装置，在风洞中开展了低质量比近壁面圆柱涡激振动试验。通过改变来流风速和间隙距离，对圆柱涡激振动特性和平板表面风压等试验现象进行了深入分析，对于近壁面圆柱涡振的试验设计以及涡振机理的研究具有参考和推动意义。

1 试验简介

1.1 模型安装与试验原理

本次试验在直流式小风洞中开展。其试验段截面尺寸为0.45 m×0.45 m×1.20 m，壁面边界层为20 mm左右，湍流度在0.5%以下，风速范围在0～40 m/s连续可调。如图1所示，圆柱模型两端铰接在尼龙张力线中央，整体模型保持水平，仅限制为横向振动。尼龙线长度足够长，可消除圆柱振动所带来的位移影响，其预张力可通过拉力器灵活调节，以获得合适的系统固有频率。圆柱两端碳纤维杆与尼龙线衔接处设置有小块木制挡板，用于反射下方激光位移器(IL-300)发出的激光，从而通过采集装置可获得圆柱的振动位移。圆柱下方设置有控制间隙距离的移动平板，其前缘设置为光滑圆弧形，以避免流动分离。

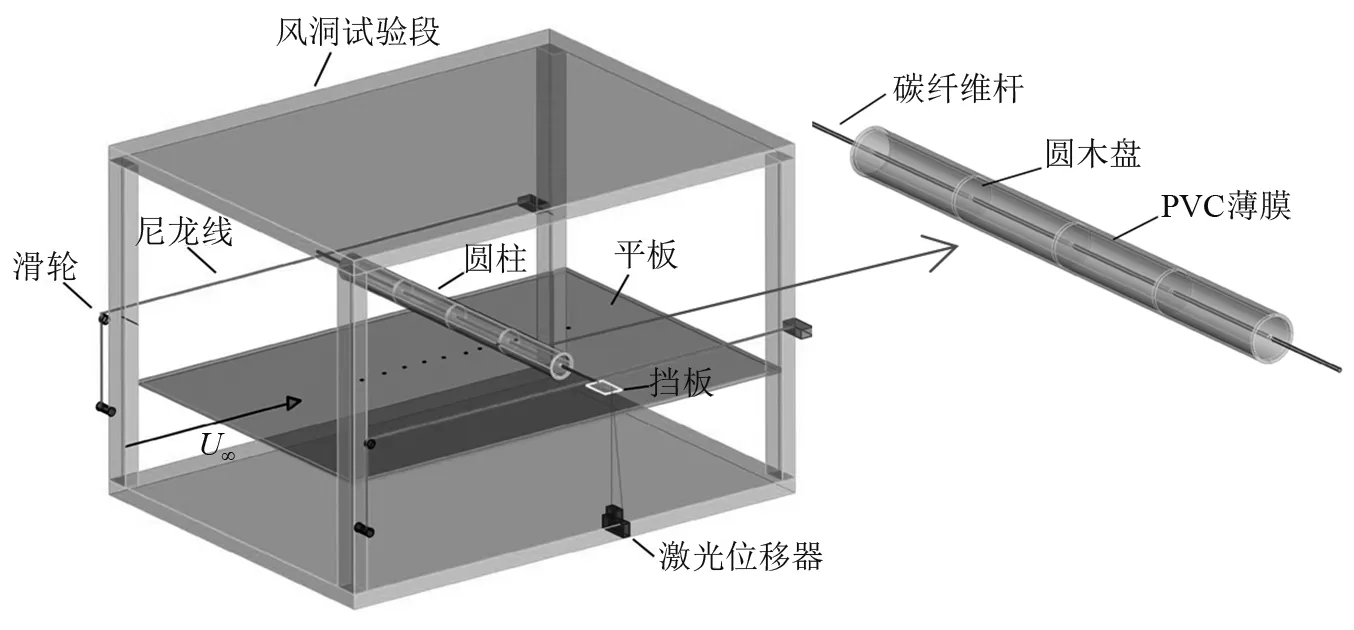
图1 模型安装示意图Fig.1 Schematic of experimental installation

模型质量比是影响试验结果的主要因素，为降低圆柱质量比，模型主体结构采用密度极低的巴尔杉木制成。整体构造类似于柱节段，由五块3 mm厚的圆木盘与碳纤维杆串联而成，其外框架采用亚光PVC薄膜蒙制。总的来说，此结构拥有着质量轻、强度高等特点，满足本次的试验要求。考虑到模型制作难度和尾流场范围，圆柱直径设计为35 mm；同时为了避免三维流动效应以及额外增加端板而带来附加质量，圆柱展长L设计为445 mm，略小于风洞宽度450 mm。

试验原理简化如图2所示，初始时，圆柱处于平衡位置，并将此时圆柱中心点定义为坐标零点，各坐标轴方向于图2中示出。随着来流U∞的施加，圆柱脱离平衡位置上下振动。此外，圆柱下方间距为S的平板表面于来流方向水平布置有12个测压孔，可以同步监测不同间隙比下振动圆柱下方平板表面的气压变化。试验定义柱体正下方测压孔为d点。离d点最近的4个测压孔间距为2 mm，其余测压孔间距为4 mm。测压孔离d点的距离定义为变量a，在试验处理中用圆柱直径D进行无量纲化。

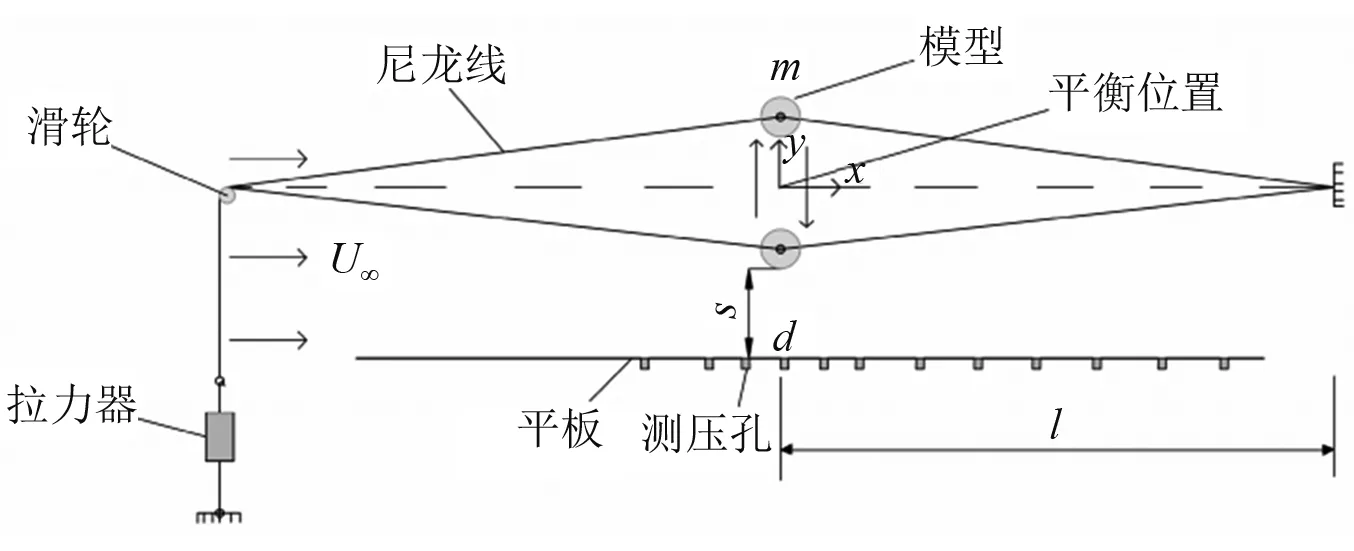
图2 试验原理图Fig.2 Diagram of experimental principle

1.2 试验相关参数

在试验开始之前，通过眼镜蛇探针(TFI-269)对空风洞下的平板表面边界层进行了标定。如图3所示，可知边界层厚度δ≈0.43D。试验其余关键参数由表1给出，其中系统固有频率和阻尼可以通过位移自由衰减曲线得出，m为圆柱和尼龙绳及木制挡板质量之和，ρ为空气密度，P0为风洞静压，P为测点平均风压，Prms为脉动风压均方根值。本次试验风速的施加规律为增速，间隔小于0.1 m/s，且每次对风速进行调节之后，均需等待足够长时间(60 s以上)，以获得圆柱达到平稳状态时的各项数据。

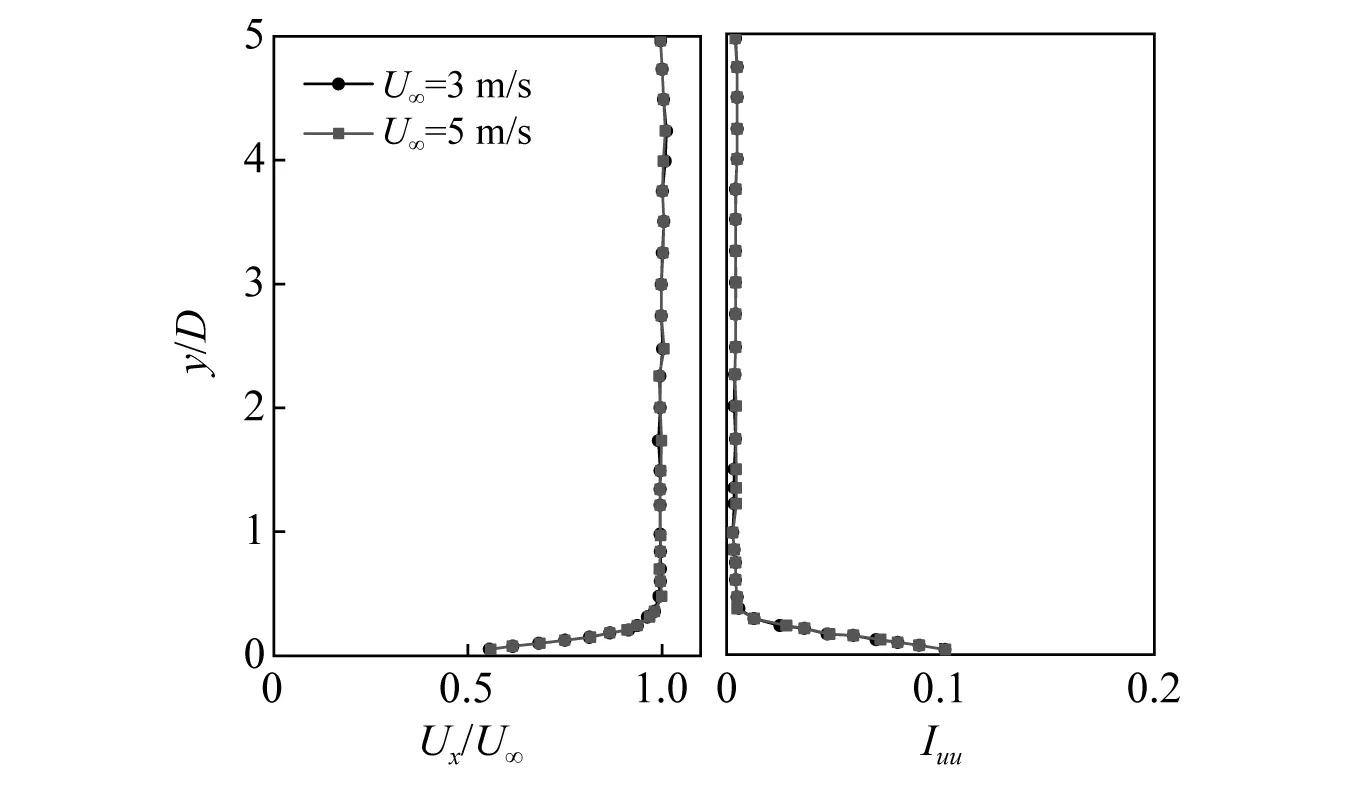
图3 平板边界层标定Fig.3 Boundary layer calibration

表1 试验参数Tab.1 Experimental parameters

2 试验结果与讨论

2.1 圆柱幅值

孤立圆柱(即无平板)幅值与频率的文献对比结果，如图4所示。可知，响应幅值的变化规律在定性上与Khalak等的研究结果是类似的，而与Feng的试验规律不同的主要原因是他的模型m*属于大质量比范畴。从频率图中可以看出，随着速度的增加，圆柱尾流涡脱符合St规律；当速度增加到一定范围内，fv/fn始终维持在1附近，这种现象被称之为锁频，其速度区间被定义为锁定区间；此后速度进一步增加，圆柱尾流涡脱又重新回到St规律。

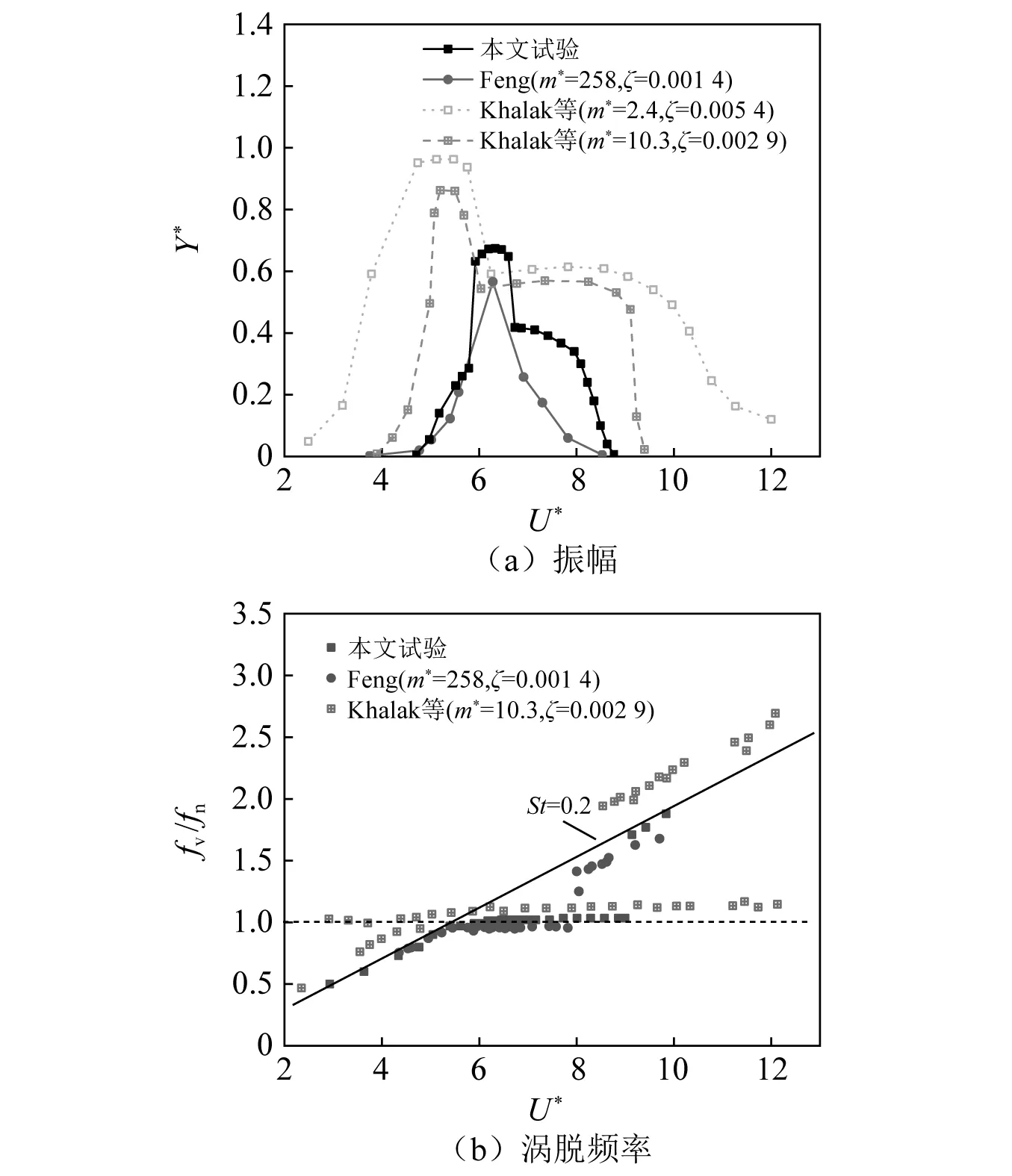
图4 文献对比Fig.4 Literature contrast

不同间隙比下圆柱的幅值响应如图5所示，并基于圆柱的最大位移响应是否与平板产生接触，将其划分为限制区(0≤S/D≤0.5)和非限制区(S/D>0.5)两个部分。在限制区内，对于S/D=0，所有风速范围内均未发生振动，其最大振幅始终为0，这与Wang等和Zhao等在水洞中所获得的试验结果并不相同；在极小间隙比S/D=0.1的情况下，其幅值曲线异于其余间隙比，它碰壁振动时的最小约化速度比其余间隙比要小，且能碰壁振动的最大约化速度远小于相邻间隙比S/D=0.2的情形；对于间隙比0.2≤S/D≤0.5，碰壁振动时的最小约化速度几乎一样，但最大约化速度随间隙比的变化呈减小趋势；对于限制区内的所有间隙比，S/D=0除外，都存在一个共同的特征，即：在碰壁振动期间，尽管圆柱的振动受限于间距，但接触壁面后柱体反弹向上所达到的振幅略高于固有的间距；此外，圆柱从微振至碰壁与从碰壁至微振这两个阶段中的过渡是非常迅速的，特别是后一个阶段，这种过渡几乎是瞬发的。

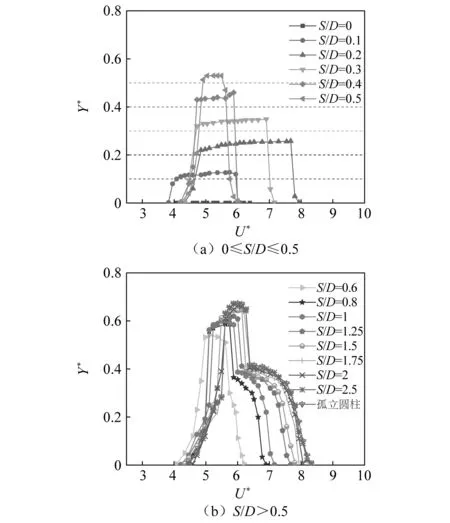
图5 响应振幅Fig.5 Amplitude of cylinder

在非限制区内，圆柱均不存在碰壁行为，且从S/D=0.8开始幅值曲线明显可见三个不同的分支，即初始分支、上分支和下分支，这有别于限制区内幅值曲线的变化规律。随着间隙比的增加，初始分支的变化并不明显，而上分支的幅值逐渐抬升，整体区间往后移动，下分支的区间逐渐扩宽，凸显更加清晰，整体区间同样向后延伸；间隙比越大，三个响应分支的变化越小，当间隙比达到2.5时，可认为圆柱振幅的三个分支与孤立圆柱的情形无异，平板对圆柱响应的影响可近似忽略。

为了更加形象的展现圆柱锁定区间与间隙比之间的关系，如图6所示，以不同的填充符号详细区分了圆柱的各个响应状态；其中实心圆曲线为圆柱进入锁定时的速度，简称锁定启动速度，空心圆曲线为圆柱离开锁定时的速度，简称锁定退出速度。值得一提的是，由于S/D=0一直处于静止状态，所以此间隙比下并不存在锁定区间。由图可知，在限制区内，圆柱在S/D=0.1时的锁定启动/退出速度明显低于相邻间隙比；其余间隙比下的锁定启动速度几乎不变，均在U*=4.4附近，而锁定退出速度持续减小，于S/D=0.5处达到最小值；此外，在限制区内，圆柱的主要响应状态为碰壁振动。对于非限制区，随着间隙比的增加，锁定启动速度变化较小，而锁定退出速度越来越大，最终在S/D=2.5 达到最大值，但曲线斜率逐渐放缓；同时，圆柱的响应开始出现三个分支，且随着间隙比的增加，初支范围微增，上支范围微减，而下支变化明显，其范围持续扩大。

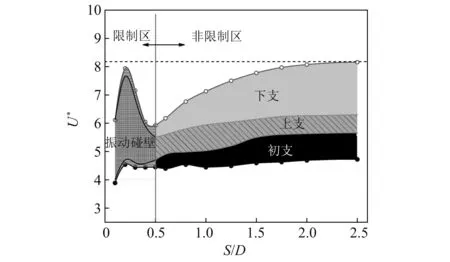
图6 锁定区间随间隙比的变化Fig.6 Variation of lock-in range to S/D

2.2 尾流形态

间隙比在影响圆柱响应的同时，也会造成圆柱尾流结构的改变；此外，圆柱不同的响应所对应的尾流形态也不一样。此次研究通过流动可视化手段(烟线)来呈现圆柱尾流的涡结构，由于篇幅有限，仅挑选两个具有代表性的间隙比。如图7所示，分别呈现了限制区(S/D=0.5)与非限制区(S/D=1.5)的尾流涡结构对比结果。对于间隙比S/D=0.5，圆柱发生碰壁振动时，由于壁面的限制，尾流中仅可见规律性的上侧涡脱，而下侧区域流体通过量较小，在圆柱的运动过程中，近尾流剪切层向上卷起，与上侧旋涡发生相互作用并融合，最终消散在远尾流当中；随着速度的增加，圆柱退出锁定区间，呈几乎静止状态，此时圆柱的尾流形态与圆柱振动的情形有所区别，即圆柱的上侧剪切层在远尾流区域才可见明显涡脱，且下侧的剪切层同样在远尾流区域才形成向上卷曲，这在He等的研究中也能看到此现象。对于间隙比S/D=1.5，此时间隙距离足以容纳圆柱下侧旋涡的发展，当U*=5.0时，圆柱振幅响应位于初始分支，上侧尾流形态与S/D=0.5的情形类似，而下侧尾流结构得以充分发展，受到壁面的影响较弱，整体流态为经典的卡门涡街(即2S模式，表示每个振动周期脱落两个单涡)。随着风速的进一步增加，响应分支由初支过渡到上支，圆柱状态转变为大幅振动，旋涡脱落于上下两侧平行排列，即平行涡模式。Morse等[21]将此平行涡模式称为“2Po”，即2S向2P转变的一种过渡形式，它出现在上分支中。继续增加试验风速，圆柱振幅发生跳跃(下支)，圆柱尾流中呈现出2P脱落模式(即每个振动周期脱落两对旋涡)，这种脱落形式一直维持至振动减弱。

图7 尾流涡结构Fig.7 Wake vortex structure

2.3 平板表面风压系数

圆柱与壁面之间的气动力作用是相互的，平板的存在影响了圆柱的响应规律以及尾流形态，同时圆柱的反馈又改变了平板表面的压力分布。在实际工程中，靠近管道系统的壁面大多都是可侵蚀性的，陆面风蚀作用或海底冲刷作用必然会影响到管道周围的流动。局限于试验条件，此次研究以间隙比作为变量代替侵蚀作用，来探讨柱体附近壁面的风压分布，具有一定的参考意义。

本节挑选了4个具有代表性的间隙比(即S/D=0.1，S/D=0.5，S/D=0.8和S/D=1.5)来阐述平板表面的风压系数特征。图8给出了这几个典型间隙比下平板表面d点(d点位于圆柱正下方，见图2)的平均风压系数Cp和脉动风压系数C′p。如图8(a)所示，当S/D=0.1时，Cp随U*的增加，整体呈“U”形曲线分布；在曲线的初端和末端，Cp的波动不大，接近为直线，主要是因为圆柱在此速度范围内几乎成静止状态；而在曲线的中部，Cp从初端迅速减小过渡到曲线底部，随后跳跃式升高至末端区域，发生这种变化的主要原因是圆柱进去锁定区间后，振幅迅速变大，振动形式为碰壁振动，当脱离锁定时便突然停止振动，从而引起Cp跳跃式转变到末端的现象。当S/D=0.5时，Cp同样呈“U”形曲线分布，但相对于S/D=0.1来说，U形区域变窄，Cp明显增大；对比图5(a)和图7(a)中的S/D=0.1的情形，不难发现，“U”形曲线的底部与圆柱碰壁振动的速度区间是相对应的，也就是说，圆柱振动时离壁面越近，Cp的值趋向于更小；所以，S/D=0.5的“U”形曲线差别于S/D=0.1的主要原因可以归结于间距的增大以及圆柱高振幅区间的缩小。随着S/D的继续增加，“U”形曲线越来越“平坦”。当S/D达到1.5时，“U”形曲线几乎呈直线，整体接近于-0.2。若S/D继续增加至2.5时，Cp值将趋近于0，此时可认为，该间隙下圆柱振动对平板表面d点风压的影响可忽略不计。

如图8(b)所示，对于C′p而言，随着U*的增加，整体曲线呈倒“U”形，变化规律与Cp相似。但不同的是，当S/D=0.5时，高振幅下的C′p比S/D=0.1大，比S/D=0.8却要小；此外，对于所有S/D，圆柱静止或微振下的C′p接近于0。

图8 不同间隙比下平板表面d点风压系数Fig.8 Pressure coefficient of point d at different S/D

为了更加详细地说明平板表面整体风压分布与圆柱不同响应状态之间的关系，图9呈现了几个典型来流速度U*下(其中不同的U*对应着不同的响应，见图6)平板表面的Cp和C′p。当S/D=0.1时，圆柱前后两侧的Cp值存在一个急剧的跃变，直至圆柱尾流较远的地方才缓慢升至平稳；且圆柱静止和振动这两种状态导致平板表面Cp的分布明显不同，振动状态下Cp的跳跃幅度相对更大；对应的C′p图中也可以发现，碰壁振动圆柱正下方的测压点(即d点)出现最强烈的脉动响应，而离d点距离越远的测压点，C′p越小，但圆柱静止时便不会出现这种现象。S/D=0.5时所得到的Cp和C′p的规律与S/D=0.1是一致的。但当S/D=0.8时，其结果略有不同，圆柱大幅振动下的Cp曲线比柱体静止时的更加平滑，且最大C′p值不再是d点，而出现在圆柱后方的测压点。此后，随着S/D的增加，圆柱两侧的Cp差距逐渐减小，当间隙增加至S/D=1.5时，Cp曲线的变化较为平缓，但圆柱两侧Cp的差距未完全消失；同时，从C′p图中也能看出，在大间隙S/D=1.5下，不论圆柱是否振动，平板表面各测点的C′p分布均未出现较大波动。

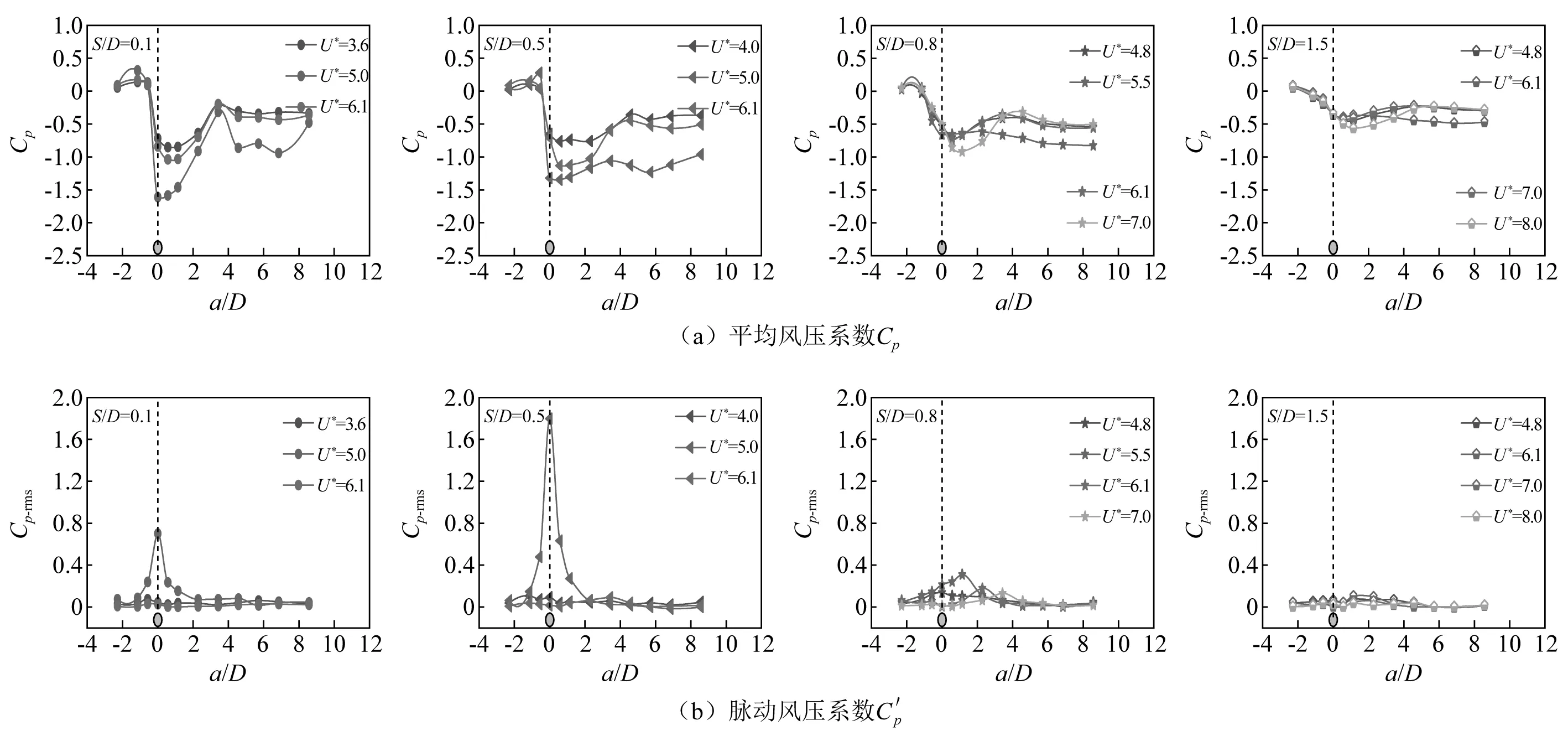
图9 不同速度下平板表面风压系数分布Fig.9 Pressure coefficient of flat surface at different velocities

2.4 响应频率

当振动的圆柱离平板较近时，其表面风压将会出现相应的周期性脉动。为了明晰圆柱响应与平板表面风压变化间的关系，图10分别给出了4个典型间隙比下圆柱涡脱频率fv、振动频率fc和d点风压脉动频率fp的对比结果，其中不同的阴影分段代表不同的圆柱响应状态。根据前人的研究可知，对于小间隙比下的静止圆柱绕流，壁面对尾流旋涡的脱落存在强烈的抑制作用。在本次研究中，对于S/D≤0.3，圆柱静止时未观察到规律性的旋涡脱落。如图10所示，对于S/D=0.1的非锁定区间，由于圆柱振幅非常小，可认为此时的流动为静止绕流，所以此部分的fv，fc与fp未能测出；而在锁定区间内，fv，fc与fp均可以测得，且三者完全重合，其频率比略高于1，说明小间隙比下的圆柱振动反而受到了平板的促进作用，这与Wang等所发现的结果是一致的。至于其余间隙比，在锁定区间外，圆柱可认为静止，其fv符合斯托罗哈率，而在锁定区间内，频率比均维持在1附近。在2.3节中有提到，平板表面风压系数的变化与圆柱振动时离平板的距离具有强相关性，也就是说，风压系数的变化是圆柱振幅以及间距综合影响的结果；所以，随着S/D的增加，fp仅在圆柱较高振幅下才能测得，而在非碰壁、初支和下支区间，存在部分范围未能捕获到fp值。

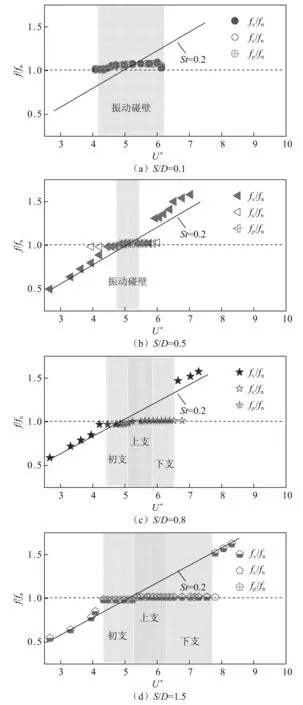
图10 响应频率对比结果Fig.10 Response frequency contrast

3 结 论

本试验利用新型张力线振子系统，消除了传统风洞涡振试验中弹簧所带来的附加质量的影响。同时基于设计的轻质圆柱，通过风洞试验研究了不同间隙比S/D下的圆柱响应以及平板表面风压系数。根据试验结果，可得出如下结论：

(1) 当S/D=0时，在所有速度范围内圆柱恒静止；当0

(2) 在极小间隙比(0≤S/D≤0.3)情况下，静止圆柱尾流的旋涡脱落被完全抑制，而振动时的旋涡脱落得以加强。通过对比S/D=0.5和S/D=1.5的圆柱尾流结构可知，较小间隙比下的圆柱尾流结构呈单侧涡街，表现形式单一；而较大间隙比下的圆柱尾流结构受平板影响小，表现形式丰富，随速度变化依次呈2S-平行涡-2P。

(3) 平板表面风压系数与圆柱振幅以及间隙比密切相关。相对于圆柱静止来说，圆柱振动时d点的平均风压系数Cp显著降低，脉动风压系数C′p显著升高；圆柱前后平板表面的Cp值存在较大的跳跃，且这种跳跃会随着圆柱的振动而加剧；随着S/D的增加，这些现象会逐渐削弱。