中低速磁浮轨道结构垂向振动传递特性研究

徐 畅，赵坪锐，徐天赐，屈超广，刘卫星，蔡文锋

(1.西南交通大学 高速铁路线路工程教育部重点实验室，成都 610031；2.中铁二院工程集团有限责任公司，成都 610031)

近年来，随着我国轨道交通的快速发展，传统轮轨交通所引起的振动与噪声对城市环境造成的污染也日益加重。目前，在振动控制要求较高的城市轨道交通中经常采用各种形式的减振型轨道作为这一问题的解决方案[1-2]。磁浮轨道交通作为一种新兴的城市轨道交通形式，以其爬坡能力强、安全性能高、振动小、噪声低、环保性能好等优点受到广泛关注[3]，具有很大的发展空间。

中低速磁浮交通系统中的耦合振动问题十分复杂，与车辆运行稳定性密切相关[4-7]，目前已有学者从悬浮控制[8-9]、车体轻量化[10]以及下部基础结构等角度对磁浮轨道系统的振动特性进行了分析，其中磁浮车辆—桥梁系统耦合振动模型被广泛使用。在磁浮轨道车辆—桥梁系统耦合振动研究中，学者一般会将模型进行简化处理，忽略磁浮轨道结构的具体形式，仅建立磁浮车辆及下部桥梁的动力学模型进行计算，分析不同桥梁形式、桥梁跨度、支座刚度及行车速度等变量对于桥梁以及车辆振动的影响。这样的处理方式往往不能体现出结构振动的真实情况。李小珍等[11-12]经过与现场测试结果的比对发现，建模时将磁浮轨道的结构形式考虑在内，会使得计算结果更加符合实际情况。周丹峰等[13]的研究也表明：磁浮轨道结构中的弹性轨排在某些条件下将引发自激振动现象，自激振动将诱发产生较大噪音并可能会导致轨道结构的疲劳破坏。

综合以上研究现状，磁浮轨道结构作为磁浮列车与下部基础的连接部分，对于磁浮轨道系统耦合振动将会产生重要影响，而目前针对中低速磁浮轨道结构本身的振动与传递特性的研究较少。因此，本文建立了中低速磁浮轨道结构有限元模型，采用谐响应分析方法从频域角度对结构垂向振动传递特性进行研究，通过与室内试验结果进行对比，验证模型正确性。此外，以结构垂向导纳、垂向位移传递率、垂向力的传递率为评价指标探究了扣件垂向刚度、阻尼、轨枕支承间距以及F轨顶面厚度对于中低速磁浮轨道结构垂向振动与传递特性的影响。以便能够为中低速磁浮轨道结构的优化设计提供参考。

1 中低速磁浮轨道特点及振动传递计算原理

1.1 中低速磁浮轨道特点

磁浮轨道交通与传统轮轨最大的区别在于其非接触运行方式，车辆环抱轨道结构运行，利用电磁间的相互作用力实现列车的悬浮、导向和驱动。如图1所示，中低速磁浮轨道结构从上到下依次为F轨、H形钢轨枕、扣件系统、承轨台以及下部基础[14]。磁浮轨道结构的特殊性使得它具有以下特点：第一，为适应车辆运行特点，F轨为外伸悬臂结构，且钢枕支承间距较大，使得其竖向刚度较小且不均匀；第二，沿线路纵向，每组轨排之间设置接头，以适应温度变化的影响。

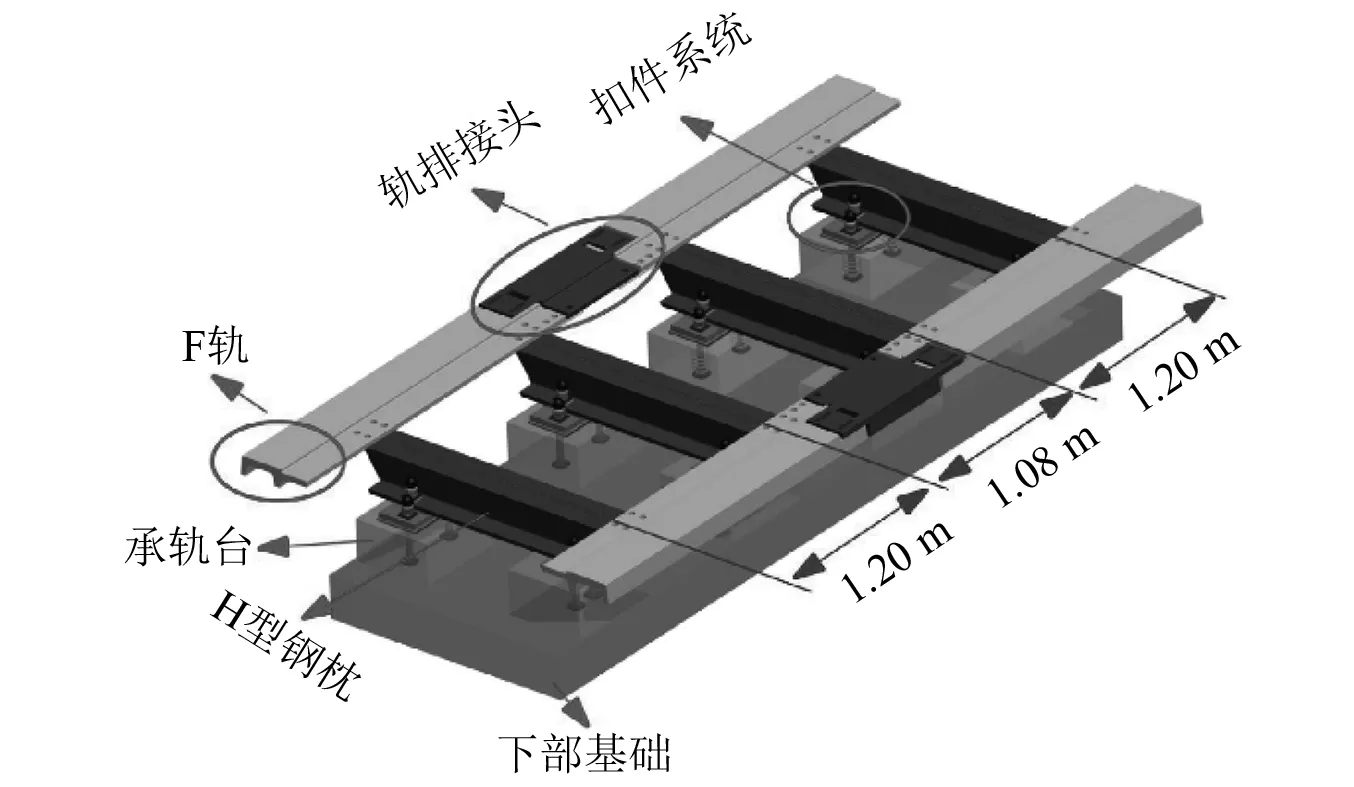
图1 中低速磁浮轨道结构示意图Fig.1 Schematic diagram of medium-low speed maglev track

1.2 振动传递计算原理

中低速磁浮轨道结构是一个多自由度系统，在计算其简谐振动稳态响应时可以用传递函数来表示系统的响应与所受激励之间的关系，传递函数不受激励的影响，仅由系统参数以及振动频率决定，当其用复数形式表示时，还可以反映出系统的频率和幅值传递特性[15-16]。因此本文采取采用谐响应分析方法对于中低速磁浮轨道结构1～500 Hz内的垂向导纳进行计算，以便研究该结构的垂向振动传递特性。简谐力激振条件下，轨道结构运动微分方程可表示为式(1)

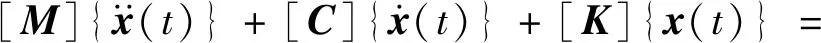
(1)

求解方程，设轨道系统复数形式的稳态响应可表示为

将试验样板放入容量1 L的气味瓶中密闭，然后放入80℃烘箱中恒温2 h。取出气味瓶冷却至室温，然后由5个评价人员进行气味等级评价，取出现次数最多的等级作为最终结果(可以取两个等级的中间值，如2.5级、3.5级)。

{x(t)}={x(ω)}eiωt

(2)

式中，{x(ω)}为位移向量。

将式(2)代入式(1)中可得

(3)

式中，H(ω)为系统的传递函数。

当系统受到的简谐激振力幅值大小为单位1时，则传递函数就是该系统的位移导纳HD(ω)。对位移导纳进行求导，可进一步求出系统的速度导纳与加速度导纳，如式(4)和式(5)所示

HV(ω)=iωHD(ω)

(4)

HA(ω)=iωHV(ω)=-ω2HD(ω)

(5)

式中：ω为圆频率；HD(ω)，HV(ω)，HA(ω)分别为系统的位移导纳、速度导纳和加速度导纳。

2 试验与模型对比验证

2.1 试验概况

试验对象为通过一组伸缩接头相连的两榀短轨排结构。总长4.68 m，轨枕间距1.2 m，接头处轨枕间距为1.08 m，下部底座板及承轨台均为现场浇筑，材料为新型高强速凝材料，以便现场施工修复。在室内对该结构垂向振动特性进行测试，试验时在结构不同位置布置加速度传感器，采用力锤施加激励，同一位置进行多次敲击，拾取结构不同部位加速度响应。经数据处理后可得到F轨的垂向加速度导纳，现场测试情况如图2所示。

图2 现场测试图片Fig.2 Field test photos

2.2 仿真计算模型

本文利用有限元软件ANSYS 建立中低速磁浮轨道的振动传递模型，着重考虑轨道结构自身的振动传递特征，并结合相关试验结果对模型结果进行验证，相关参数取值如表1所示，具体几何尺寸如图3所示。

表1 模型参数Tab.1 Model parameters

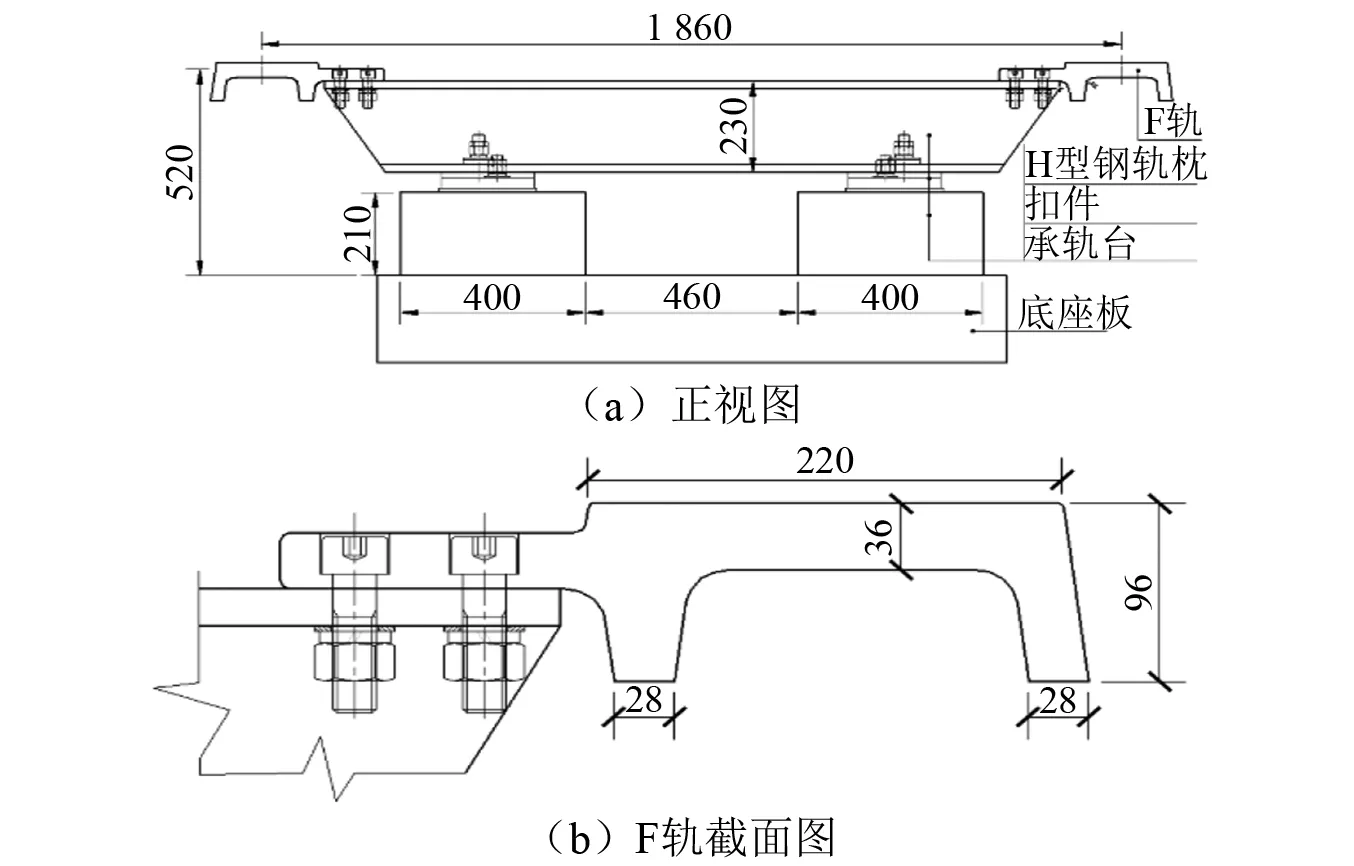
图3 中低速磁浮轨道尺寸图(mm)Fig.3 Dimensions of medium-low speed maglev track (mm)

其中F轨、承轨台以及下部底座板均按照实际尺寸采用实体单元进行模拟，扣件系统以及下部基础简化为离散的弹簧—阻尼单元，将伸缩接头视为与F轨为一个整体考虑。网格划分时在轨枕与F轨过渡处进行适当加密处理。结构有限元模型如图4所示。

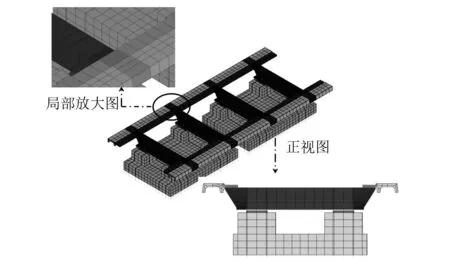
图4 有限元模型Fig.4 Finite element model

2.3 模型与试验对比

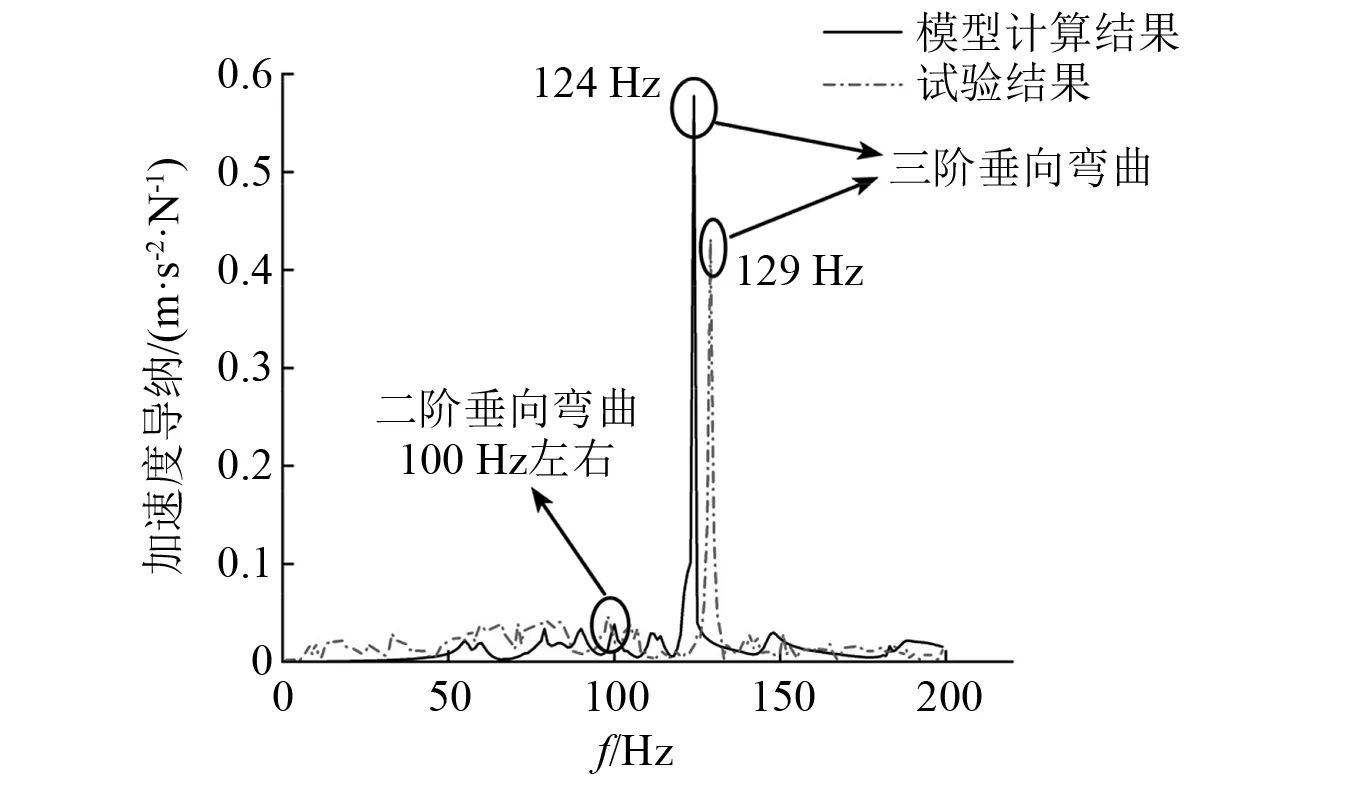
图5 加速度导纳试验与仿真曲线Fig.5 Measured and simulated curves of the acceleration admittance

3 垂向振动传递分析

3.1 垂向导纳特性分析

为了与真实情况更加贴近，同时节省计算时间，建立了长度为12 m的半边轨道结构模型，在跨中施加单位激振力，对结构1～500 Hz内的导纳特性进行计算分析。加载点及响应输出点位置如图6所示，其中1点，2点，3点，4点均相距半个轨枕间距。计算结果与结构部分模态如图7和图8所示。由图7和图8可以看出：

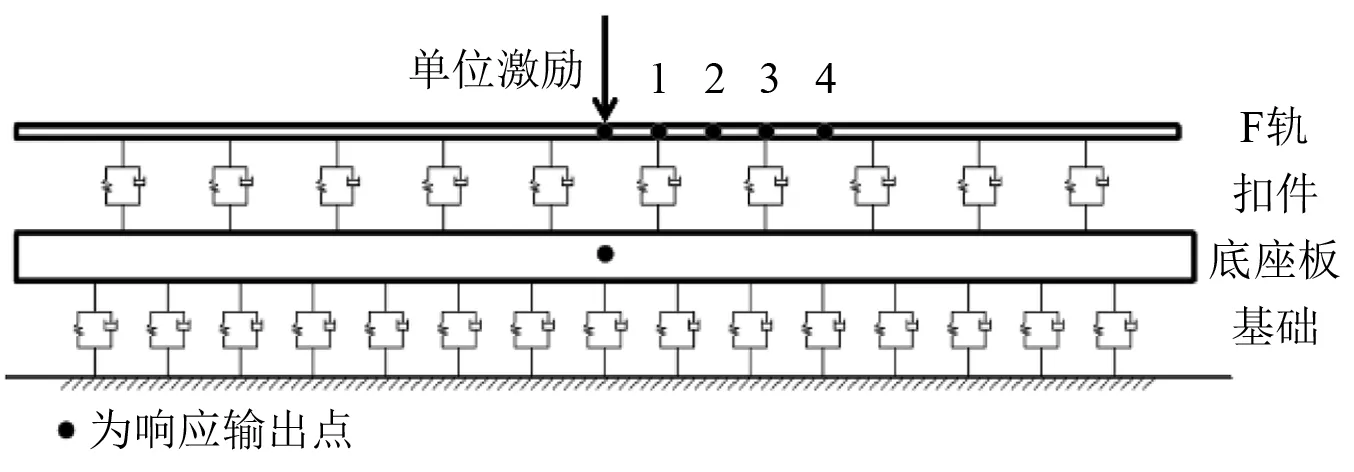
图6 模型激励位置与响应位置Fig.6 Model excitation position and response position

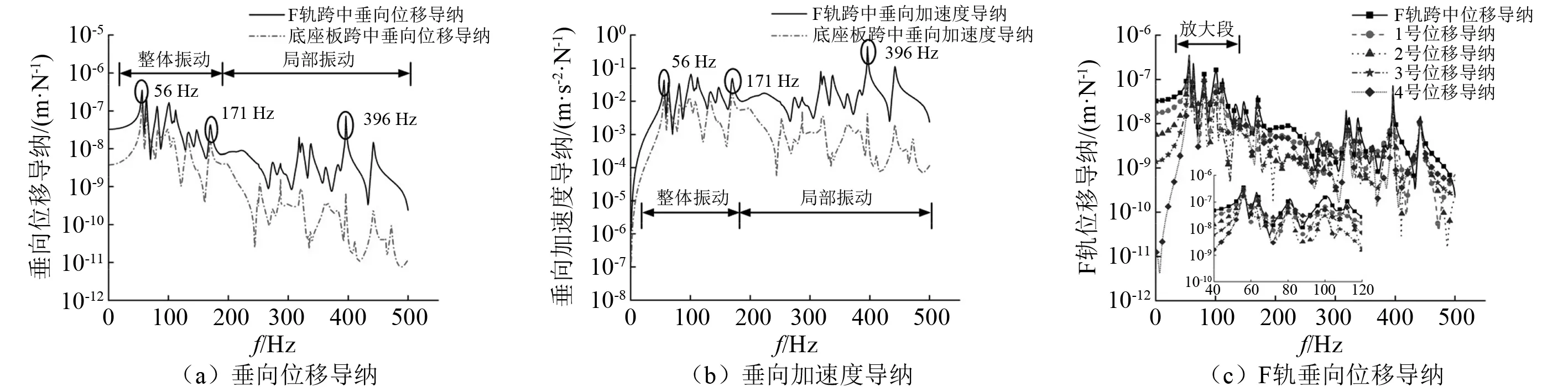
图7 结构垂向导纳Fig.7 Vertical admittance of structure

图8 结构部分模态Fig.8 Partial modes of structures

(1) 中低速磁浮轨道结构垂向振动导纳峰值较多，并且随着激振频率增加，结构位移导纳整体呈现下降趋势，加速度导纳则呈现上升趋势，与其计算公式相符。这是因为结构高频振动引起的加速度较大，但对于位移导纳贡献较小。

(2) 结构垂向振动表现为低频整体弯曲振动与高频局部振动两部分的叠加。结构在180 Hz以下的低频范围，F轨与下部底座板主要表现为垂向弯曲振动，其中，56 Hz为结构整体的一阶弯曲振动，171 Hz对应结构的高阶弯曲振动。在此范围内，F轨与下部底座板位移导纳、加速度导纳峰值接近且F轨峰值稍大于下部底座板。因为F轨为外伸悬臂结构，发生整体弯曲振动的同时还会附加扭转振动。

(3) 在180 Hz以上的频率范围内，轨道结构垂向振动以F轨及轨枕部位的局部振动为主，下部结构基本不参与振动。随着激振频率增加，F轨与底座板的位移导纳以及加速度导纳差值越来越大，最大可达近三个数量级。这是由于中低速磁浮轨道结构中F轨为悬臂状态且支承间距较短，容易发生波长较短、波数较多的局部振动，而此频率范围内的底座板响应基本由F轨局部振动向下传递引起，因此差距较大。与传统轮轨制式轨道振动相比，F轨局部振动频率较低，且振型较为密集，并且在396 Hz处，F轨垂向振动出现“pinned—pinned”共振现象。

由图9可以看出，F轨垂向振动沿结构纵向上的传递特点。在100 Hz以下的低频范围内，结构整体垂向弯曲振动波长大于两个轨枕间距，因此F轨垂向位移导纳差别不大。而随着激励频率不断增加，在结构高频局部振动阶段，F轨的垂向位移导纳沿结构纵向波动较大，纵向各点位移导纳并非简单的随着与激励点距离增大而减小。这是因为F轨在此频率范围内的振型较多，位移导纳与结构在不同频率下的振型相关。

3.2 力与位移的垂向传递特性分析

以力与位移的垂向传递率为评价指标，进一步探究频域范围内磁浮轨道垂向振动传递特性[17]。定义位移传递率HT为模型跨中加载点正下方底座板的位移导与加载点F轨的位移导纳与加载点的比值，表达为对数形式为

(6)

式中，HD1，HD2分别为底座板与F轨的位移导纳。

定义力的传递率FT为对模型跨中施加激励时，相邻扣件弹簧支反力与激振力的比值，其对数形式表示为

(7)

式中：F1为与激励点相邻的扣件弹簧支反力；F为激振力。

模型位移与力的垂向传递率计算结果如图9和图10所示。

由图9可以看出，随着频率增加，位移传递率曲线整体呈现下降趋势，且峰值频率与自振频率相比略有滞后。在低频整体弯曲振动阶段，曲线波动较小，在前几阶波峰超过0的位置，F轨跨中位置在此频率下无振型，下部底座板带动F轨振动。频率到达局部振动阶段时(180 Hz)，曲线迅速下降且波动较大，在pinned—pinned共振频率附近，F轨跨中位置振幅最大，因而曲线出现波谷。说明扣件系统低频范围内的隔振性能较差，垂向振动主要沿竖向传递。

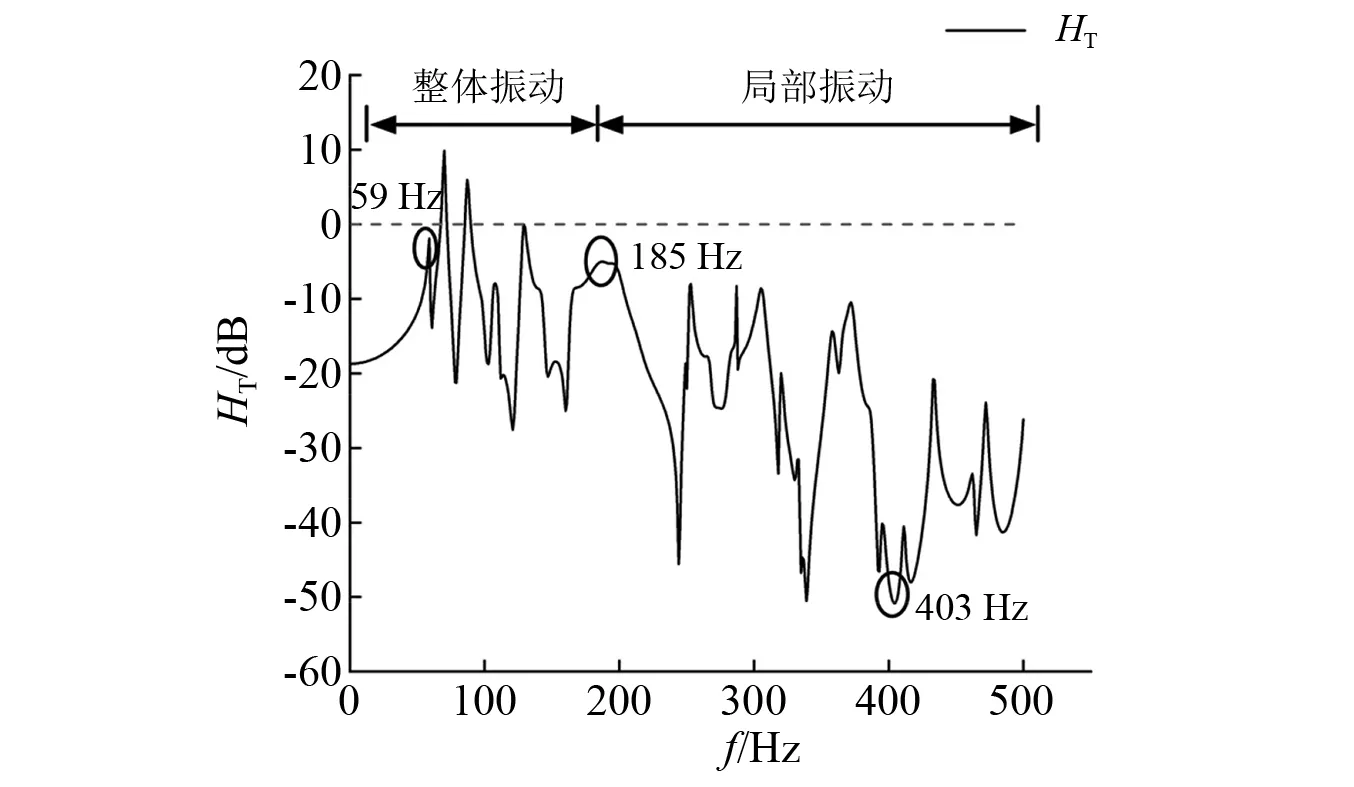
图9 位移垂向传递率Fig.9 Vertical transmissibility of displacement

由图10可以看出，力的传递率曲线整体上随着频率增加呈现下降趋势，并且波峰较为密集，说明不同频率下力的变化比位移更加敏感。在低频整体振动阶段，力的传递率峰值大都超过0。说明在此频率范围内，力在向下传递的过程中会被放大，下部结构的受力状态变差。到高频局部振动阶段(180 Hz)时，曲线峰值大幅下降，但由于F轨局部pinned—pinned共振的存在，曲线在该位置出现较大峰值。

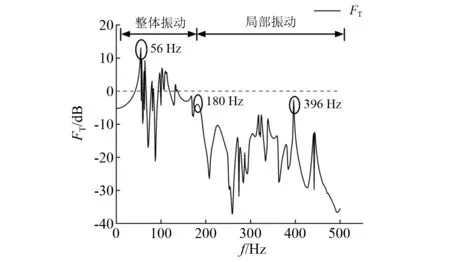
图10 力的垂向传递率Fig.10 Vertical transmissibility of force

4 影响因素分析

4.1 扣件垂向刚度

分别计算扣件垂向刚度为50 kN/mm，100 kN/mm，200 kN/mm，300 kN/mm以及500 kN/mm时对于结构垂向振动传递的影响，结果如图11和图12所示。从图11和图12可发现，扣件垂向刚度增加增强了结构之间的耦合作用，使得结构垂向位移与力的传递率曲线的峰值均增大且峰值频率向右移动。这说明随着扣件垂向刚度的增加，系统垂向隔振性能整体减弱。传递率曲线的峰值及峰值频率在局部振动阶段增幅均比整体振动阶段大，说明扣件刚度对于结构高频范围内垂向传递的影响更大。因此在满足结构挠度的前提下，应适当选取较小的扣件垂向刚度值。

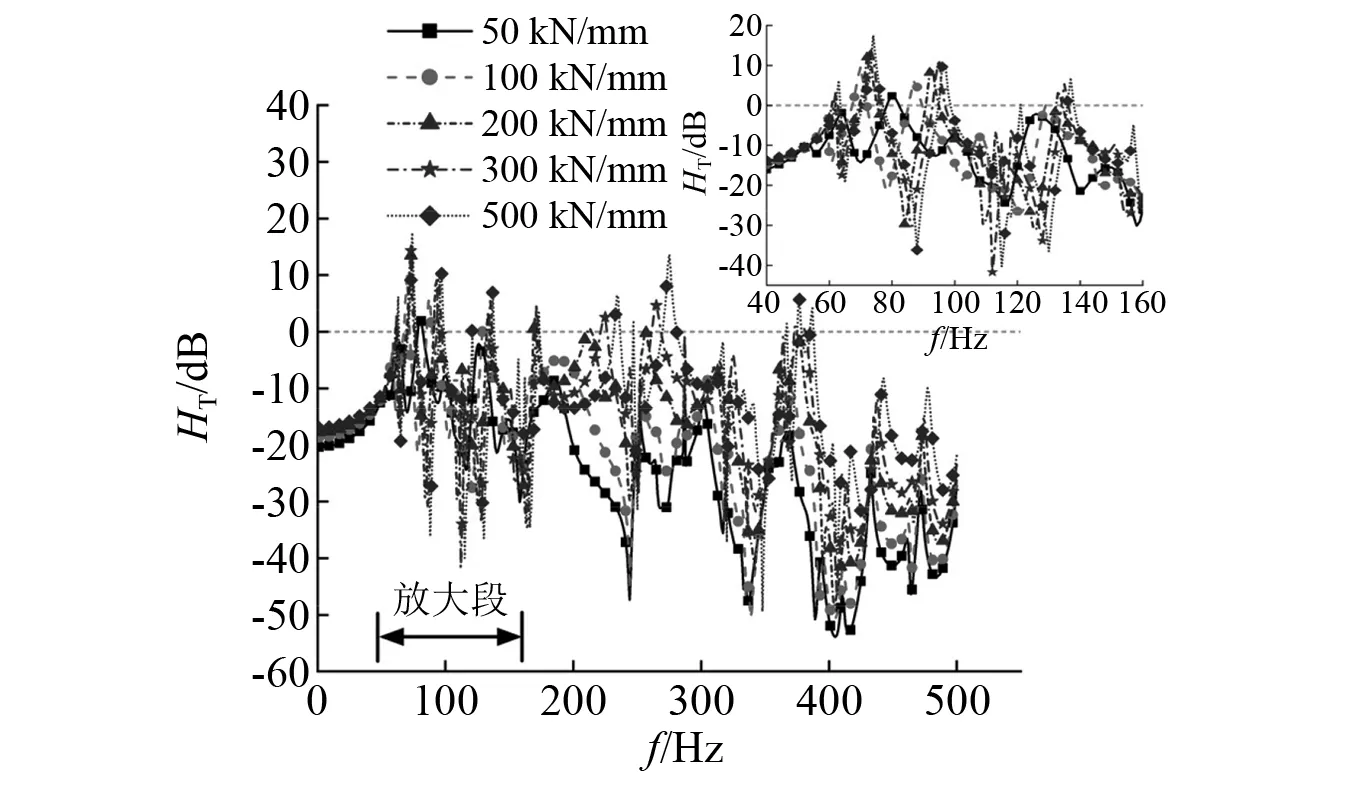
图11 不同扣件刚度位移传递率Fig.11 Displacement transmissibility of different fastener stiffness

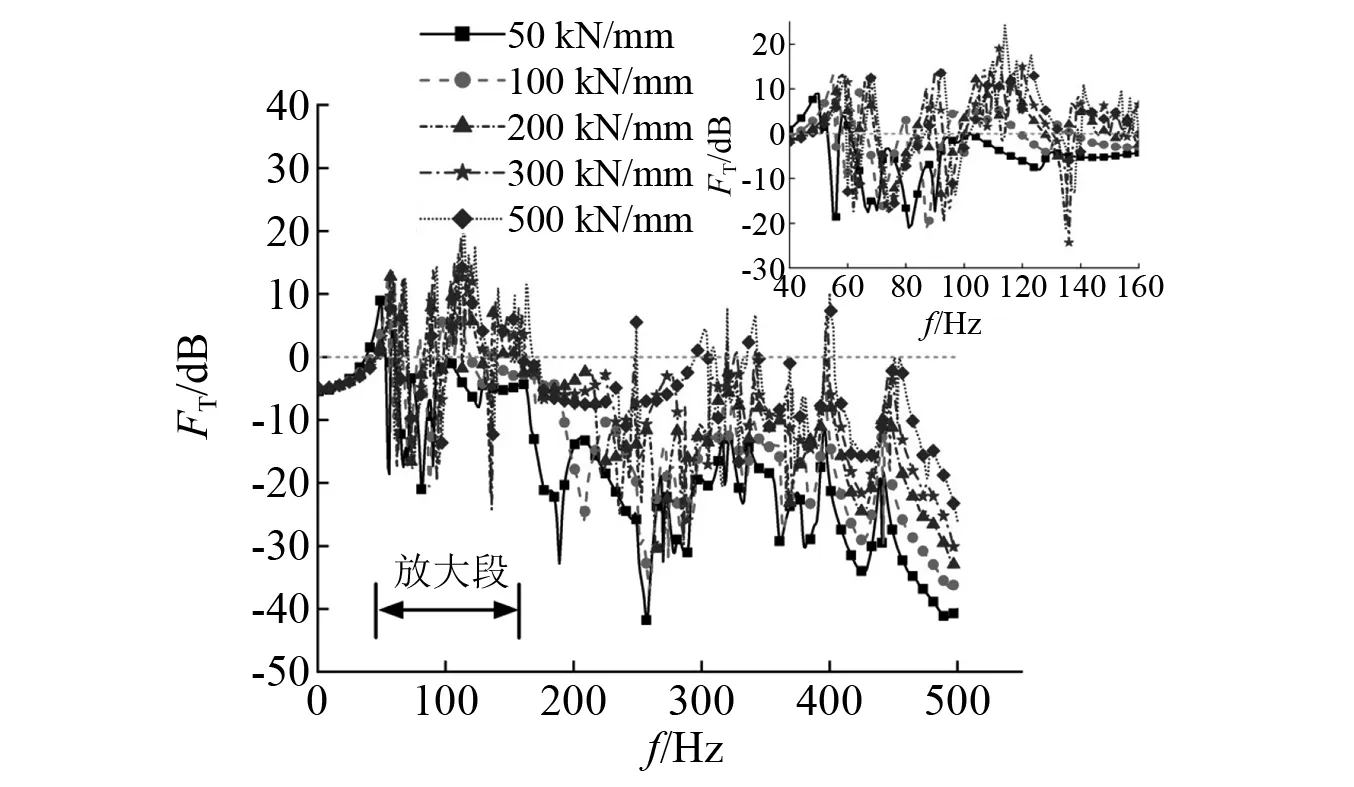
图12 不同扣件刚度力的传递率Fig.12 Force transmissibility of different fastener stiffness

4.2 扣件垂向阻尼

扣件阻尼是结构振动计算中的重要参数，影响振动传递。选取扣件阻尼值分别为10 kN·s/m，20 kN·s/m，30 kN·s/m，50 kN·s/m，70 kN·s/m进行计算。位移与力的传递率结果如图13和图14所示。由图13和图14可以看出，扣件垂向阻尼增大会显著抑制轨道结构垂向振动，减小结构垂向位移与力的传递率曲线峰值大小，但基本不影响峰值频率，在高频振动段，阻尼对于力的传递率抑制作用比位移更加明显。放大图中可以发现，垂向阻尼较大时，系统振动能量耗散较快，会使得有些垂向变化较小的曲线峰值消失，减少了曲线波动。

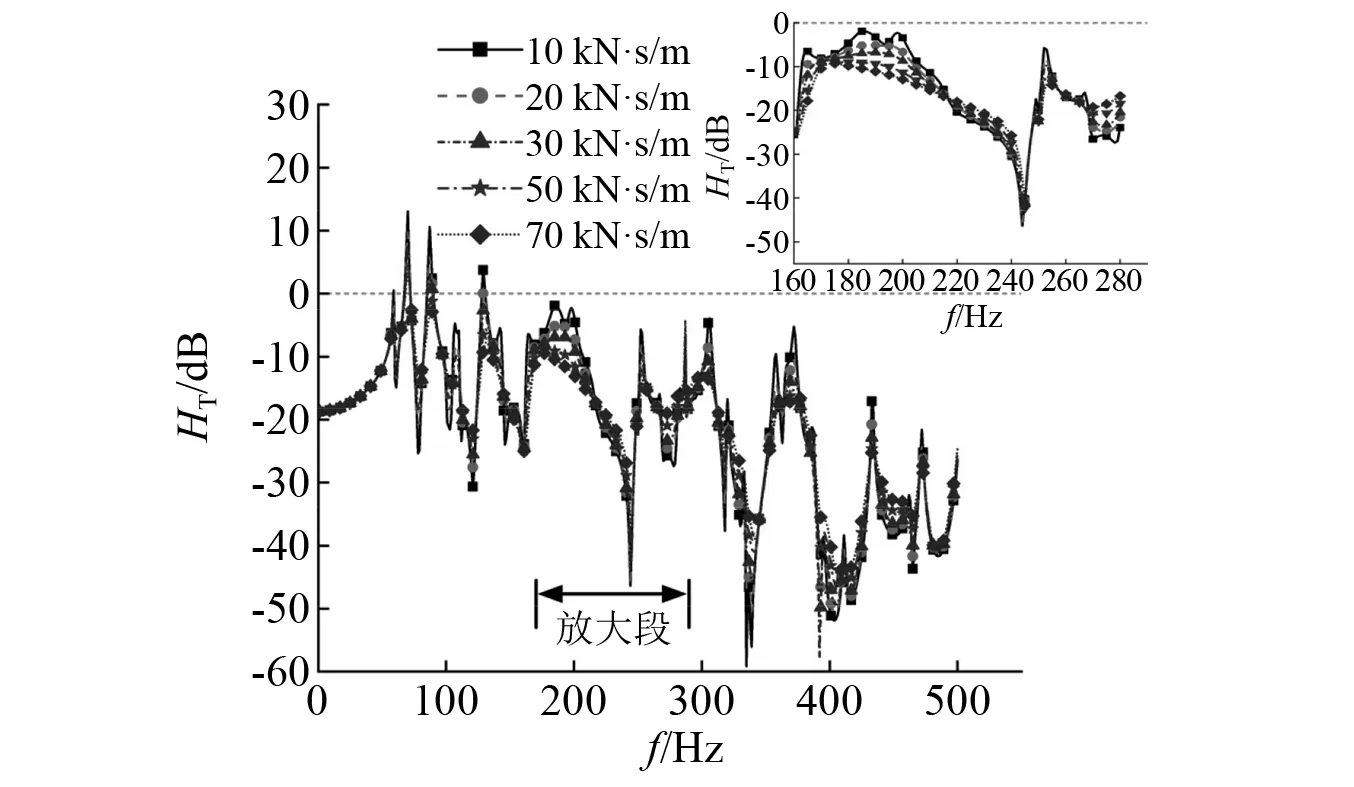
图13 不同扣件阻尼位移传递率Fig.13 Displacement transmissibility of different fastener damping

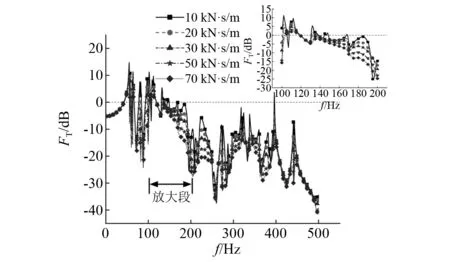
图14 不同扣件阻尼力的传递率Fig.14 Force transmissibility of different fastener damping

4.3 轨枕支承间距

轨枕支承间距变化会使得磁浮轨道结构垂向刚度改变，选取不同轨枕间距值：0.8 m，1.2 m，1.6 m，分析轨道结构垂向振动传递的变化规律，结果如图15和图16所示。结果表明：轨枕间距的增加减弱了结构垂向刚度值，使得曲线中的小波峰增多，说明引起结构垂向位移的振型增多。轨枕间距的改变主要影响结构局部振动频率大小而对于传递率曲线峰值频率处幅值影响不大。结合模态分析可以发现，轨枕间距为0.8 m，1.2 m，1.6 m时，F轨局部振动出现的频率显著减小(局部振动频率附近，位移与力的传递率明显下降，峰值接近0且位移传递率曲线频率略有滞后)，三种轨枕间距下F轨局部振动出现频率大致为200 Hz，180 Hz与150 Hz。

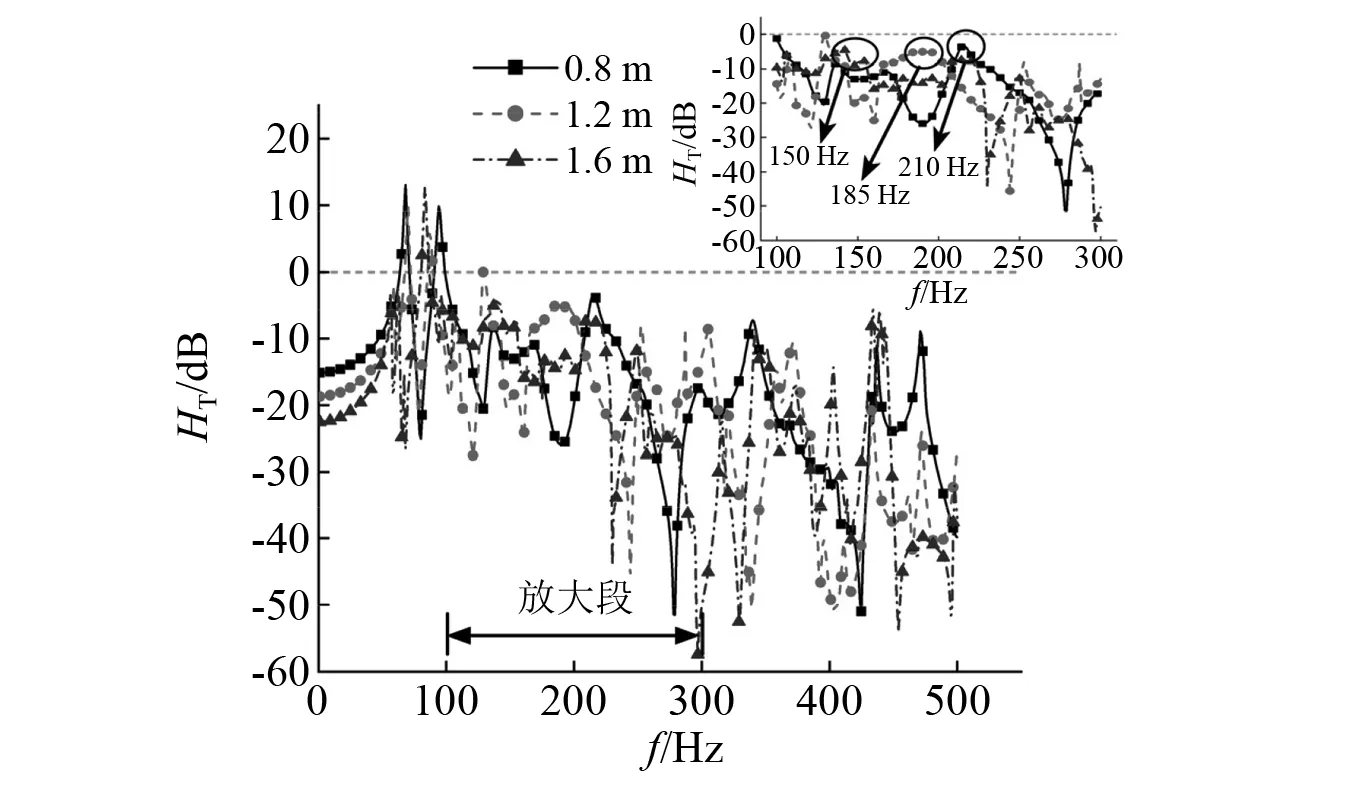
图15 不同轨枕间距位移传递率Fig.15 Displacement transmissibility of different sleeper spacing

图16 不同轨枕间距力的传递率Fig.16 Force transmissibility of different sleeper spacing

4.4 F轨顶面厚度

分别选取30 mm，36 mm，42 mm，48 mm，54 mm的F轨顶面厚度进行计算，结果如图17和图18所示。随着F轨顶面厚度的增加，结构位移传递率峰值大小逐渐增加，力的传递率峰值大小则逐渐降低，两个曲线的峰值频率均有所增加。F轨顶面厚度变化对结构高频局部振动范围内的影响更为显著。这是因为F轨顶板厚度的增加增大了其自身垂向刚度，导致F轨垂向变形量减小，更难发生局部振动。

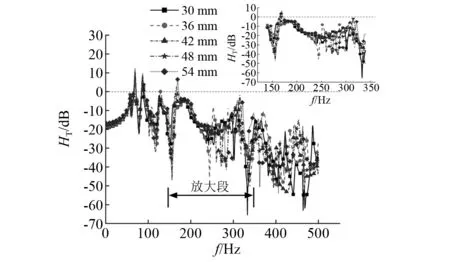
图17 不同F轨顶面厚度位移传递率Fig.17 Displacement transmissibility of different top thickness of F-rail

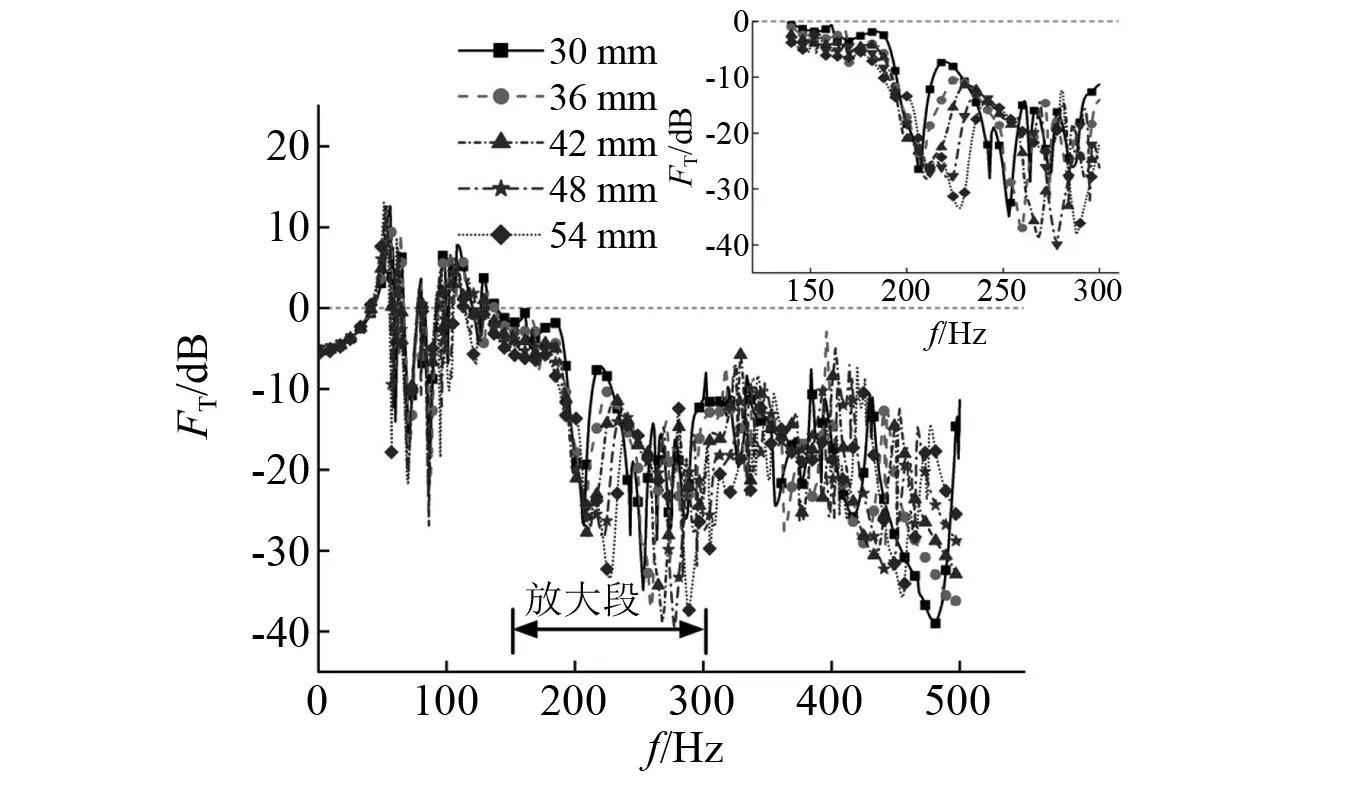
图18 不同F轨顶面厚度力的传递率Fig.18 Force transmissibility of different top thickness of F-rail

4.5 轨枕翼缘厚度

分别选取14 mm，17 mm，20 mm，23 mm，26 mm的轨枕上下翼缘厚度值进行计算，结果如图19和图20所示。结果表明：轨枕上下翼缘厚度增加对于结构振动垂向传递的影响与轨枕间距减小的影响相似，随着轨枕上下翼缘厚度的增加，在结构整体振动阶段传递率曲线基本不变，在F轨的高频局部振动阶段传递率曲线峰值频率逐渐增大，而曲线峰值大小变化很小，且轨枕上下翼缘厚度的影响频率更高。

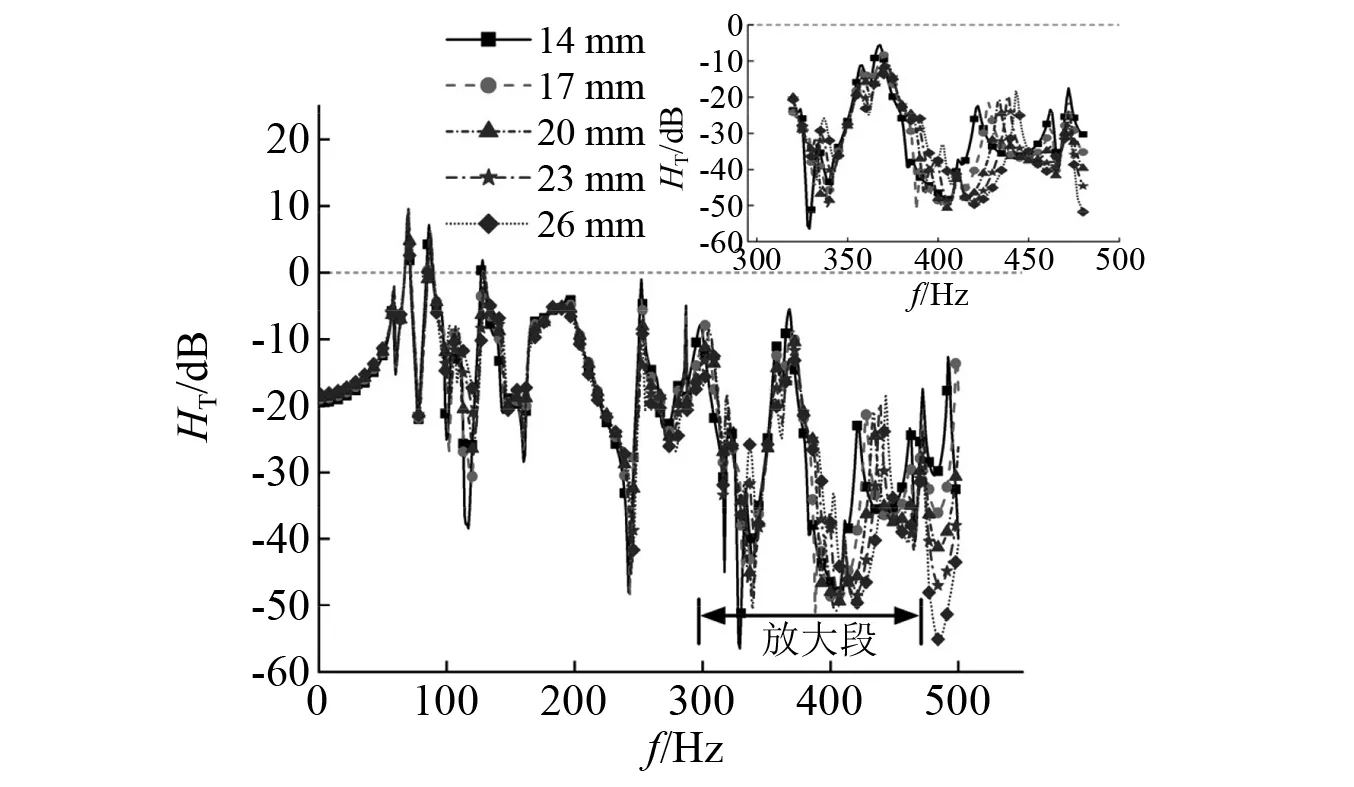
图19 不同轨枕翼缘厚度位移传递率Fig.19 Displacement transmissibility of different sleeper flange thickness

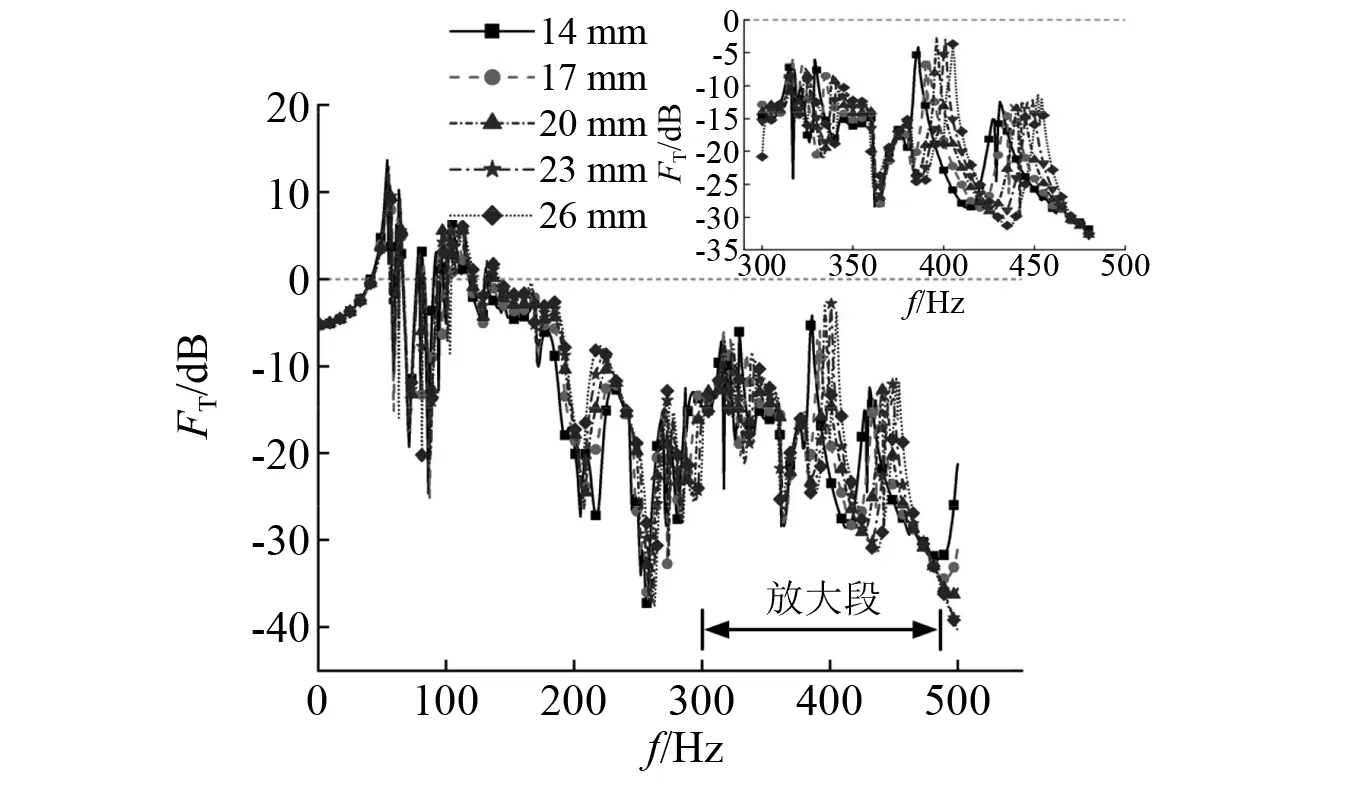
图20 不同轨枕翼缘厚度力的传递率Fig.20 Force transmissibility of different sleeper flange thickness

5 结 论

本文围绕中低速磁浮轨道结构的垂向振动与传递问题，基于轨道结构的室内试验开展了有限元数值模拟，并分析了部分结构参数对于垂向振动与传递特性的影响，主要结论如下：

(1) 中低速磁浮轨道垂向振动主要可分为低频整体弯曲振动与F轨高频局部振动两个阶段，并且结构低频段力与位移的垂向传递率较高，高频振动却很难向下传递。与传统轮轨制式相比，F轨高频振动出现频率较低且振型密集，应重视F轨对于结构的振动影响。

(2) 在频域范围内，F轨沿结构纵向上的垂向位移导纳变化并非随着与激励点距离的增大而减小，而是与结构在不同频率下的振型有关。

(3) 扣件垂向阻尼的增大基本不改变结构垂向传递峰值频率，但会减小结构在频域范围的振动幅值，并对于结构高频范围内力的垂向传递作用抑制明显。

(4) 不同影响因素均会引起结构不同部位垂向刚度的变化，从而影响结构的垂向振动传递特性。扣件刚度的增加导致力与位移的垂向传递率峰值大小与峰值频率均增大。轨枕支承间距增大，只对F轨的局部振动频率有抑制作用。F轨顶板厚度的增加则使得结构位移传递率曲线峰值减少，力的传递率曲线峰值增加，并增大了F轨的局部振动频率。轨枕翼缘厚度增加会增大高频范围内传递率曲线峰值频率，但基本不影响峰值大小。

(5) 各因素中扣件垂向刚度、轨枕支承间距和F轨顶面厚度对于结构垂向模态以及垂向振动传递特性有较大影响，应重点关注。而轨枕的翼缘厚度与扣件垂向阻尼则影响较小。