磁流变冲击缓冲系统最优广义宾汉数控制
王 成,王目凯,于 东,陈照波,闫 辉
(1.北京卫星制造厂有限公司,北京 100191;2.哈尔滨工业大学 机电工程学院,哈尔滨 150001)
最大限度地减少传递到负载的冲击载荷是现代运载器设计中的一个重要课题[1]。当运载器在恶劣的环境中运行时,过大的冲击载荷会对运载器上的设备或人员造成损伤[2-4]。现在的运载器一般采用被动式吸能器来吸收冲击能量。被动式吸能器一般依靠材料塑性变形制成[5],其载荷行程曲线固定,针对单一负载或固定的冲击强度设计,无法适应负载质量或者冲击强度发生变化的工况[6],Mikuowski等[7]提出了一种主动液压式吸能器,通过液压伺服,能够根据需求自适应调节输出载荷。但是这种设备引入庞大的伺服机构并且需要添加反馈控制带来了潜在的不稳定性。
磁流变缓冲器(magnetorheological shock absorber,MRSA)作为一种智能器件,具有结构简单、尺寸和质量小、能耗低、响应速度快、阻尼力可调范围大的优点,被认为是最理想的半主动耗能器件[8]。磁流变缓冲器在结构上可以看作是一种特殊的液压油吸能器,不同之处在于磁流变缓冲器内部装有可控的磁流变液。磁流变液是将微纳米级的铁磁颗粒(一般为羰基铁颗粒)沉浸在非磁性载液中所形成的悬浮液[9]。磁流变缓冲器的活塞上内嵌有电磁线圈,通过控制电磁线圈的输入电流,可以调节磁流变缓冲器环形间隙内的磁场强度。环形间隙内磁流变液的剪切屈服强度可以通过调节外加电流的大小来加以控制。与之相对应的是磁流变缓冲器的输出载荷可由外加电流控制。
基于磁流变缓冲器的冲击缓冲系统的研究重点在于控制策略的设计。为了最大限度地降低负载冲击载荷,必须充分利用磁流变缓冲器的行程,实现软着陆的控制目标,即活塞运动至行程末端速度降为0。Wereley等[10]提出了最优宾汉数控制策略,通过计算整个冲击缓冲过程中的最优库仑力,实现软着陆的目标。在此基础上,Saleh等[11]通过计算最优宾汉数实现直升机起落架的冲击防护。Choi等[12]提出了考虑磁流变缓冲器响应时间的最优宾汉数控制策略。Wang等[13]提出了一种最短伤害极限暴露控制策略,将最优宾汉数控制应用于高速冲击。然而,这种最优宾汉数控制策略是在磁流变缓冲器的线性阻尼模型的基础上提出的。在高速冲击下,磁流变缓冲器环形间隙内雷诺数超过2 000,磁流变液的流动状态开始由层流转变为紊流状态[14],磁流变缓冲器输出的阻尼力与活塞速度呈现近似的二次型关系[15]。
针对磁流变冲击缓冲系统,本文提出了考虑磁流变缓冲器二次型阻尼特性的最优广义宾汉数(generalized Bingham number,GBN)控制策略。首先,研制了一种双线圈式磁流变缓冲器,通过高速冲击试验测试了其阻尼力特性;然后,以软着陆为控制目标,设计了考虑二次型阻尼特性的最优广义宾汉数控制策略,分析了磁流变冲击缓冲系统在最优广义宾汉数下的软着陆效果;最后,搭建了落锤冲击缓冲快速控制试验平台,通过试验对比了线性宾汉数控制策略和二次型广义宾汉数的控制效果。
1 冲击载荷下磁流变缓冲器的阻尼力
双线圈式传统磁流变缓冲器结构原理,如图1所示。磁流变缓冲器由活塞杆、活塞、液压缸以及充满缸筒内部的磁流变液组成。活塞上留有环形液体间隙,活塞杆受振动或冲击载荷作用迫使磁流变液流过该环形间隙,活塞左右两腔室产生压力差,进而在活塞表面形成阻尼力。在液体间隙的内侧嵌入电磁线圈,当线圈通入外加电流时,环形间隙内部产生垂直穿越液体流动方向的磁场。在磁场作用下,磁流变液的磁性颗粒在磁场方向上聚集成链。间隙内的液体流动时必须剪切磁链,因此活塞表面的压力差增加,磁流变缓冲器输出的阻尼力也随之增加。
根据图1中的原理图研制磁流变缓冲器,设计参数如表1所示。研制的磁流变缓冲器组件照片如图2所示。
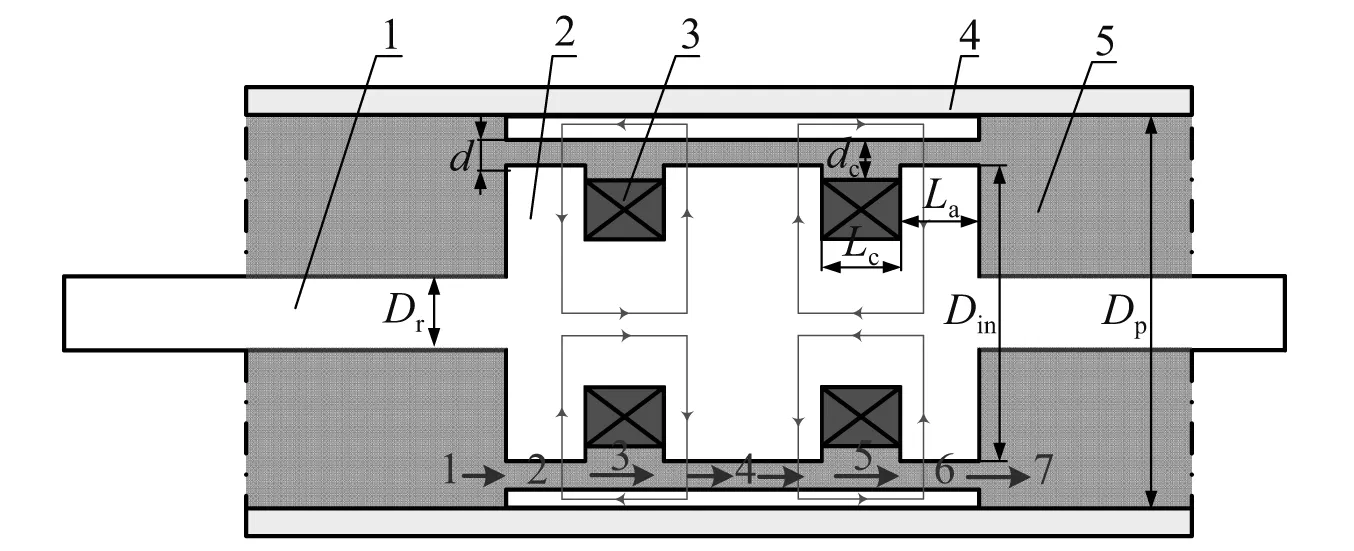
1.活塞杆;2.活塞;3.线圈;4.液压缸;5.磁流变液。图1 磁流变缓冲器结构原理图Fig.1 Schematic diagram of the MRSA

表1 磁流变缓冲器的设计参数Tab.1 The design parameter of MRSA

图2 磁流变缓冲器的组件照片Fig.2 Component photo of MRSA
1.1 磁流变缓冲器的冲击阻尼力模型
相比于活塞头的有效横截面积,环形液体间隙的通道横截面积比较小,因此当活塞运动时,环形液体间隙内磁流变液流动速度较大。在高速冲击下,磁流变缓冲器活塞速度较大,间隙内部磁流变液的实际运动状态也尤为复杂。Singh等[16]考虑磁流变缓冲器液体紊流效应对阻尼力的影响,建立了含有局部损耗的宾汉塑性(Bingham plastic minor,BPM)阻尼力模型,利用环形液体间隙内磁流变液的雷诺数来分析磁流变液的运动状态。根据BPM模型,磁流变缓冲器的阻尼力可以表示为
F=(ΔPη+ΔPml)Ap+(ΔPτAp+Ff)sign(Vp)
(1)
式中:ΔPη为因液体黏性产生的压降;ΔPml为因间隙横截面积变化带来的压头损失产生的压降;ΔPτ为因磁流变效应产生的剪切屈服压降;Ap为活塞有效横截面积;Ff为磁流变缓冲器的摩擦力。
由式(1)可知,磁流变缓冲器活塞表面的压降由黏性压降ΔPη、剪切屈服压降ΔPτ和局部水头损失压降ΔPml组成。其中,剪切屈服压降ΔPτ与环形间隙内液体流动状态无关,而黏性压降ΔPη和局部水头损失压降ΔPml与液体流动状态有关。仿真过程中忽略磁流变缓冲器的摩擦力,磁流变缓冲器的零场压降可以表示为
ΔPfield-off=ΔPη+ΔPml
(2)
当磁流变缓冲器通入电流时,磁流变缓冲器的压降可以表示为
ΔPfield-on=ΔPfield-off+ΔPτ
(3)
磁流变缓冲器的黏性压降可以表示为
(4)
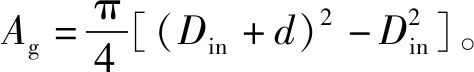
环形间隙内磁流变液的雷诺数可以表示为
(5)
式中,η为磁流变液黏度。
环形间隙内磁流变液的流动状态与磁流变液的雷诺数有关。由式(5)可知,磁流变液的雷诺数与活塞运动速度成正比。当活塞运动速度较小,环形间隙内液体雷诺数Re≤2 000时,磁流变液处于层流状态,此时达西摩擦因数可以表示为
(6)
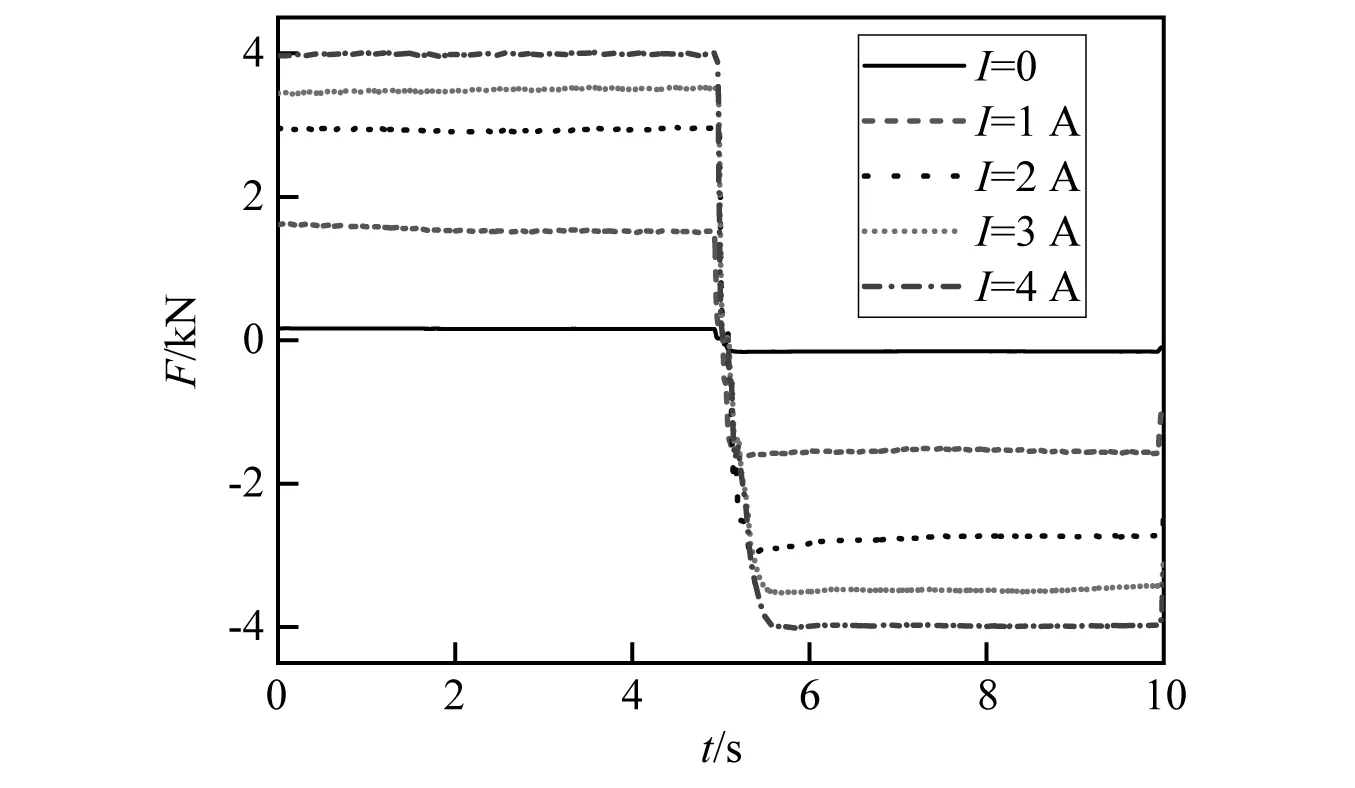
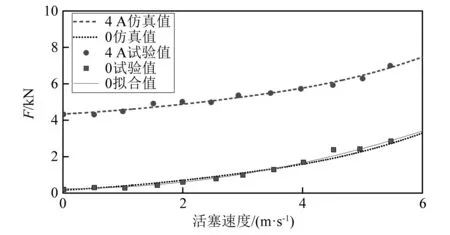
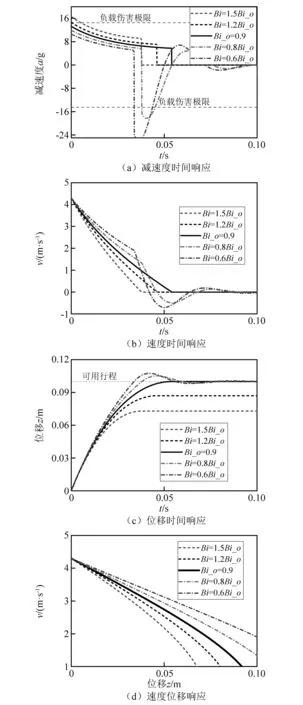
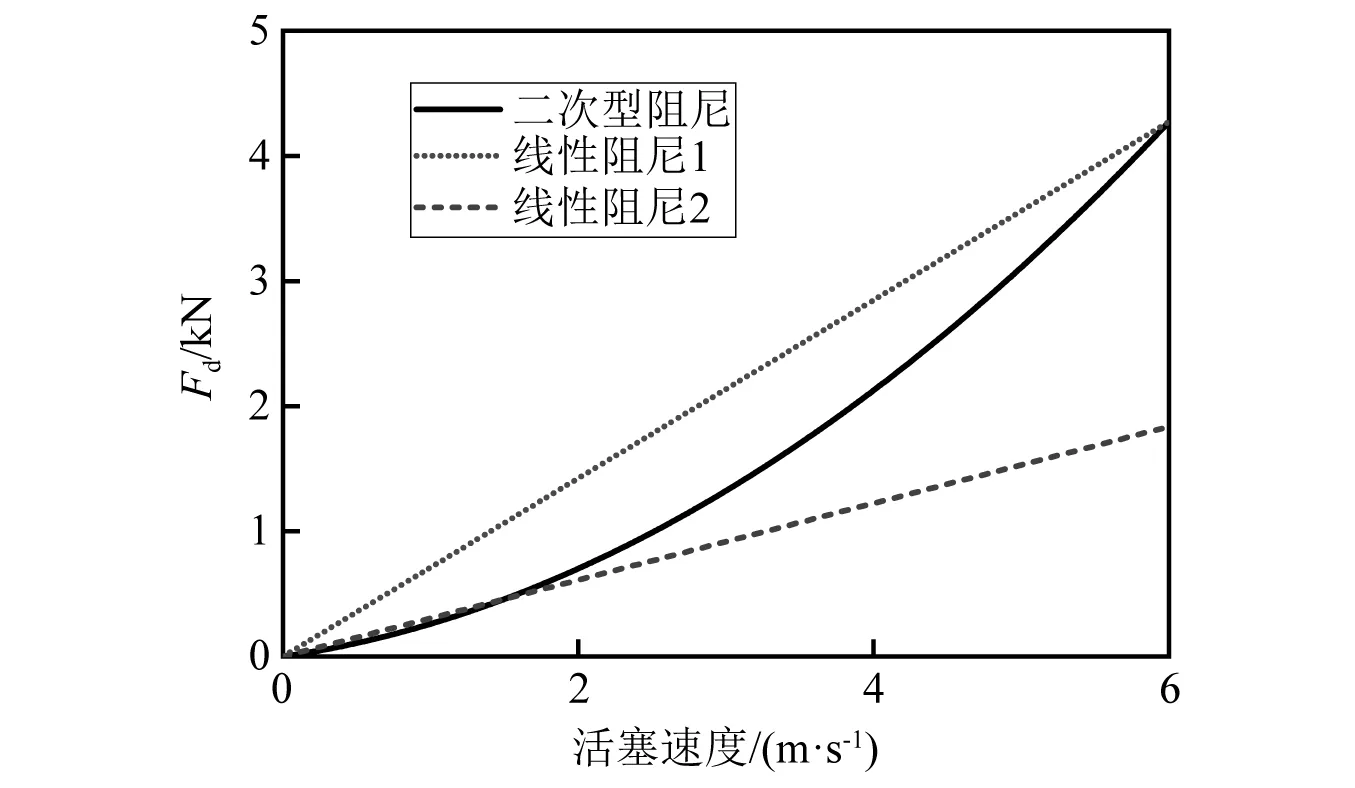
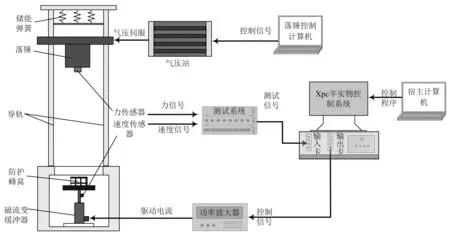
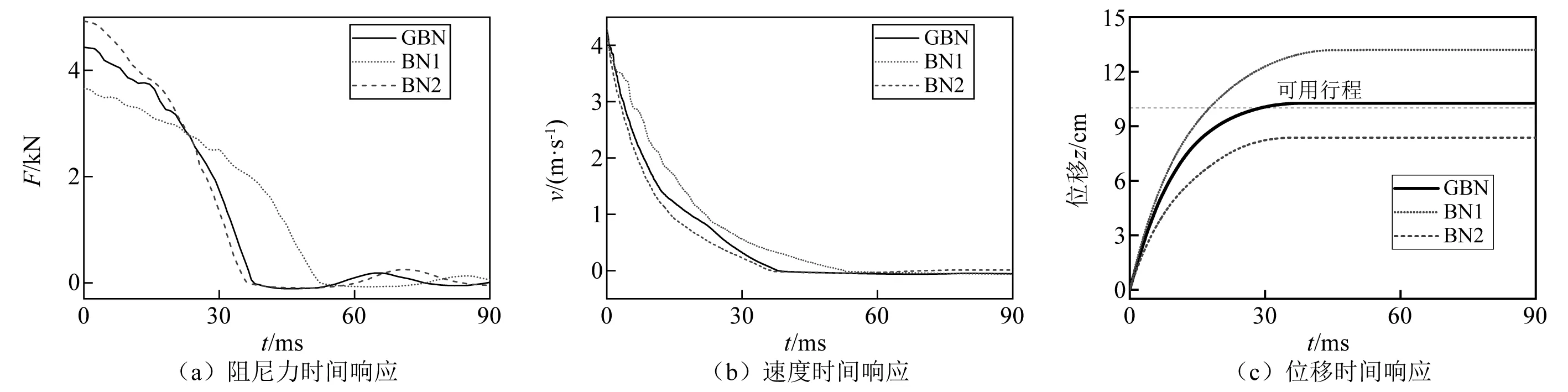
当环形间隙内液体雷诺数2 000 (7) 当磁流变缓冲器活塞运动速度较大,环形间隙内液体雷诺数Re>4 000时,环形间隙内磁流变液处于紊流状态,此时达西摩擦因数应当满足 (8) 磁流变缓冲器因局部水头损失产生的压降ΔPml也与环形间隙内液体流动状态有关。在流体力学中局部水头损失主要是由于通道的形状和大小发生变化而产生的。本文磁流变缓冲器的局部水头损失主要包括:区域1-2的通道入口效应产生的压降ΔPml12、区域2-3通道突然扩张产生的压降ΔPml23、区域3-4通道突然收缩产生的压降ΔPml34、区域4-5通道突然扩张产生的压降ΔPml45、区域5-6通道突然收缩产生的压降ΔPml56、区域6-7通道出口效应产生的压降ΔPml67。磁流变缓冲器的局部水头损失压降可以表示为 ΔPml=ΔPml12+ΔPml23+ΔPml34+ (9) 式中,各部分的压降可以表示为 (10) 式中,KEN,KSE,KSC和KEX分别为环形间隙通道入口系数、通道突然扩张系数、通道突然收缩系数和通道出口系数。根据经验公式,各系数可以表示为 (11) 式中,Ac为线圈间隙横截面积,可以表示为Ac= 1.2.1 磁流变缓冲器的库仑力测试 磁流变缓冲器的库仑力测试试验台,如图 3所示。试验使用长春机械科学研究院生产的CRIMS电液伺服疲劳试验机,利用配套的操作软件DynaTestExpert来完成磁流变缓冲器激励控制和数据采集。试验机作动器最大位移为±27.5 mm,函数发生器频率范围为0.001~100 Hz,力传感器的量程为1~10 kN。磁流变缓冲器的上下两端通过疲劳试验机的上下横梁的夹头安装;通过液压工作站对磁流变缓冲器进行激励;力传感器固定在上夹头与上横梁之间用于采集力信号;磁流变缓冲器通过电流源进行供电。 图3 磁流变缓冲器阻尼力测试系统Fig.3 Damping force test system for MRSA 磁流变缓冲器的输出力除了包括黏滞阻尼力Fv和库仑力FMR之外,还包括缓冲器密封对活塞杆产生的摩擦力Fc。其中,黏滞阻尼力Fv与活塞速度有关,而库仑力FMR和摩擦力Fc与活塞速度无关。为了准确测量磁流变缓冲器的摩擦力Fc和库仑力FMR,磁流变缓冲器的活塞应该工作在较低的速度。因此,本试验对磁流变缓冲器采用低频三角波位移激励。磁流变缓冲器在三角波位移激励下的阻尼力响应,如图4所示。三角波位移激励的幅值为z=20 mm,频率为f=0.05 Hz。在每1/4个周期内,活塞速度为v=4fz=0.004 m/s。在该激励下,无外加电流(I=0)作用时,磁流变缓冲器输出的阻尼力可以近似为摩擦力Fc。由图 4可知,本文研制的磁流变缓冲器摩擦力为Fc=0.16 kN。图4中同时给出了三角波激励下磁流变缓冲器在不同外加电流下的阻尼力。当外加电流I=1 A时,磁流变缓冲器输出的阻尼力为FMR=1.6 kN。随着外加电流的增加,磁流变缓冲器输出的阻尼力逐渐增加;当外加电流Imax=4 A时,磁流变缓冲器输出的阻尼力可达FMR= 3.96 kN。 图4 三角波激励下的磁流变缓冲器的库仑力Fig.4 The MRSA yield force characteristic under triangular excitation 在外加电流作用下,磁流变缓冲器的库仑力FMR可以用磁流变缓冲器输出的阻尼力F与摩擦力Fc的差值表示,即FMR=F-Fc。磁流变缓冲器输出的库仑力随外加电流的变化情况,如图5所示。试验依旧采用三角位移激励,幅值为20 mm,频率为0.05 Hz。为了方便后续进行磁流变缓冲器控制方法的研究,现对库仑力进行多项式拟合 FMR(I)=0.052I4-0.401 6I3+ (12) 磁流变缓冲器库仑力的试验值与拟合值的对比图,如图5所示。由图5可知,式(12)的对磁流变缓冲器的库仑力的拟合效果较好。 图5 库仑力与外加电流关系图Fig.5 Yield force vs.applied current 1.2.2 高速冲击激励下的阻尼力特性 磁流变缓冲器高速落锤试验测试系统,如图6所示。图6中落锤试验机采用INSTRON公司提供的CEAST 9350标准落锤冲击试验机,该试验机由落锤冲击系统和数据采集系统组成。落锤冲击系统的主体是落锤机架,包含锤头、横梁以及可以作为配重的附加质量。落锤机架的质量就是整个跌落质量,冲击能量等于落锤机架与试件接触时刻的动能。数据采集系统包括数据采集仪、速度传感器和力传感器。整个冲击过程中的冲击力和冲击速度由力传感器和速度传感器实时记录,并由数据采集系仪进行采集,由控制计算机记录。 图6 磁流变缓冲器高速落锤试验测试系统Fig.6 MRSA high-speed drop hammer experiment set up 磁流变缓冲器在不同活塞速度下的阻尼力特性,如图7所示。磁流变缓冲器阻尼力的仿真值由BPM模型计算得到。由图7可知,BPM模型的仿真结果与试验结果匹配较好,因此BPM模型可以准确地表示磁流变缓冲器的高速冲击下的阻尼力特性。当磁流变缓冲器两线圈通入4 A的电流,在相同活塞速度下磁流变缓冲器输出的阻尼力较零场(0)下大得多。试验中活塞最大速度为5.5 m/s。当活塞速度为5.5 m/s,通入4 A 电流时,磁流变缓冲器输出的阻尼力可达6.99 kN,是零场下输出阻尼力(2.85 kN)的2.45倍。 图7 磁流变缓冲器阻尼力速度关系Fig.7 MRSA damping force vs.velocity 单自由度磁流变冲击缓冲系统原理如图8所示,以磁流变缓冲器活塞杆的初始位置为基准线,负载质量为m,负载初始冲击速度为v0,方向向下为正,磁流变缓冲器可用行程为Sav。 图8 单自由度磁流变冲击缓冲系统原理图Fig.8 Configuration of the shock mitigation system with an MRSA 基于磁流变缓冲器的单自由度冲击缓冲系统的动力学方程为 (13) 初始条件可以表示为 (14) fd(t)=c1v2(t)+c2v(t)+fmr(t) (15) 将式(15)代入式(13),磁流变冲击防护系统的动力学方程可以表示为 (16) 考虑二次型阻尼特性的磁流变冲击缓冲系统的软着陆控制目标是:寻找磁流变缓冲器输出的最优库仑力或者最优可控阻尼力。为了表示方便,磁流变缓冲器输出的阻尼力可用量纲一化的参数——广义宾汉数来表示;广义宾汉数定义为可控阻尼力与二次型的零场阻尼力的比值 (17) 将式(16)中单自由度冲击缓冲动力学方程表示为速度的形式,整理得 (18) (19) 对式(18)进行积分,并代入初始条件v(t=0)=v0,可得冲击缓冲过程负载速度 (20) 进一步对式(20)进行积分,并代入初始条件z(t=0)=0,可得冲击缓冲过程负载位移 (21) 为了实现软着陆的控制目标,在冲击缓冲结束时刻负载位移应该到达磁流变缓冲器可用行程,且负载速度降为0。假设总的冲击缓冲时间为t0,在t=t0时刻,负载速度和位移分别为v(t=t0)=0,z(t=t0)=Sav。分别代入式(20)和式(21)可得 (22) (23) 系统的仿真参数如表 2所示,其中缓冲器参数由第1章落锤试验测量得到。 表2 系统仿真参数Tab.2 The system parameters for simulation 图9表示初始冲击速度4.3 m/s下,考虑磁流变缓冲器二次型阻尼特性时磁流变冲击缓冲系统在不同广义宾汉数下的动态响应对比,负载质量为32.6 kg。对比的目的是为了揭露控制器输出的最优宾汉数的控制效果优于其他宾汉数(Bi>Bi_o或者Bi 由式(22)和式(23)联立计算求得最优广义宾汉数Bi_o=0.9,此时磁流变缓冲器输出的最优剪切阻尼力为2.15 kN。在最优广义宾汉数下,如图9(b)和图9(c)所示在0.054 s,负载位移到达磁流变缓冲器的可用行程0.1 m,此时速度正好降为0,可以实现软着陆的要求。 如式(17)所示,随着广义宾汉数的增加,磁流变缓冲器的可控阻尼力也随之增加。当系统控制器输出的广义宾汉数大于其最优值(Bi>Bi_o)时,磁流变缓冲器输出过大的阻尼力,系统处于过阻尼状态。当系统控制器输出的宾汉数Bi=1.5Bi_o时,此时由式(17)计算得磁流变缓冲器输出的库仑力为3.23 kN,大于最优广义宾汉数下输出的最优库仑力(见图9)。在过阻尼宾汉数的控制下,负载位移到达磁流变缓冲器0.073 m的行程处,磁流变缓冲器已经耗散完整个系统能量,负载速度降为0,无法实现软着陆的要求。在这种情况下,因磁流变缓冲器输出过大的阻尼力导致负载在冲击缓冲开始阶段的负载加速度高达16.6g,超过了最优广义宾汉数控制下的13.2g,这将大大增加了负载的受损概率。 图9 磁流变冲击防护系统在不同广义宾汉数下的响应Fig.9 The dynamic response of the MR shock mitigation system with different GBN 当系统控制器输出的宾汉数小于其最优值(Bi 在不同初始冲击速度下,冲击缓冲系统在最优广义宾汉数下的动态响应,如图10所示。随着冲击缓冲的进行,负载处于减速状态,负载速度逐渐减小,式(15)中磁流变缓冲器黏性阻尼力减小,负载减速度也随之逐渐降低。由图 10可知,随着初始冲击速度增加,系统动能增加,因此需要磁流变缓冲器输出较大阻尼力来耗散系统能量,从而导致负载减速度也随之增加(见图10(a))。由图10(b)可知,对于任意初始冲击速度,磁流变冲击缓冲系统在最优广义宾汉数下,负载位移到达磁流变缓冲器可用行程0.1 m处,速度降为0,也就是说均可实现软着陆的控制目标。 图10 最优广义宾汉数下,磁流变冲击缓冲系统在不同初始冲击速度的动态响应Fig.10 The dynamic response of drop-induced shock mitigation system at different initial drop velocities with optimal GBN Wereley等提出了线性宾汉数控制策略,该控制策略基于磁流变缓冲器的线性阻尼求得。对比分析磁流变缓冲器的线性模型和非线性模型,如图11所示。由第1章分析可知,在高速冲击下,磁流变缓冲器节流通道内液体流动状态由层流转为紊流,磁流变缓冲器的阻尼力急剧增加,此时阻尼力与速度特性曲线表现为二次型关系。为了明确分析线性和非线性阻尼模型的控制效果,图11给出了2种线性阻尼模型的阻尼力随活塞速度的变化曲线,2种线性阻尼系数分别为712.1 N·s/m和306.2 N·s/m。基于线性阻尼1、线性阻尼2最优宾汉数控制器分别计为BN1和BN2。 图11 磁流变缓冲器的线性和非线性阻尼力特性对比Fig.11 Comparison of linear and nonlinear damping force characteristics of MRSA 单自由度冲击缓冲系统在线性宾汉数和二次型广义宾汉数下的动态响应,如图12所示。当初始冲击速度为4.3 m/s时,线性阻尼模型1的零场阻尼力大于实际零场阻尼力。这造成了由BN1输出的库仑力小于实际的最优值,系统处于欠阻尼状态。在这种情况下,负载到达磁流变缓冲器的可用行程时负载存在非零的速度,出现触底现象。在BN1下,负载到达磁流变缓冲器可用行程处仍保留有1.67 m/s的速度,引起防触底弹簧-质量-阻尼工作,负载产生最大为22.7g的加速度,这会对负载造成伤害。 BN2控制器输出的库仑力大于实际的最优值,系统处于过阻尼状态。在BN2控制下,负载位移到达0.09 m 处速度降为0,无法实现软着陆的要求(见图12(c))。 图12 冲击缓冲系统在不同控制器下的响应Fig.12 Dynamic response of shock mitigation system under different controller 对于线性系统求取的最优宾汉数作用于磁流变冲击缓冲系统,受阻尼力模型的限制负载会出现触底冲击或者不能完全利用完磁流变缓冲器可用行程的现象。 为了验证2.2节所设计的冲击缓冲系统的广义宾汉数控制策略的软着陆效果,本章搭建落锤冲击缓冲快速控制试验平台,开展磁流变冲击缓冲系统半主动控制试验研究。试验平台工作原理如图13所示,试验现场照片如图14所示。 图13 落锤冲击缓冲快速控制试验平台原理图Fig.13 The diagram of semi-active drop hammer shock mitigation for rapid control 图14 落锤冲击缓冲快速控制试验平台Fig.14 Semi-active drop hammer shock mitigation for rapid control experiment set up 试验平台的机械部分采用INSTRON公司提供的CEAST 9350落锤试验机,缓冲器的安装方式、试验台具体原理和操作步骤已在1.2节作出详细介绍。本章所设计的试验台与落锤试验的不同之处在于电控系统。落锤冲击缓冲快速控制试验平台的电控系统包括:传感器、控制计算机、Xpc实时控制系统、测试仪器以及为磁流变缓冲器供电的功率放大器。其中,Xpc实时控制系统是整个试验台控制系统的核心部件,包括:A/D采集卡、D/A输出卡、目标计算机和宿主计算机。A/D采集卡选用美国NI公司生产的NI PCI-6259信号采集卡进行A/D转换,将输入的模拟信号转化为数字信号。采用NI PCI-6733作为D/A转换的输出板卡,将输出的数字信号转换成模拟信号。选用研华610H工控机作为目标计算机,其主板自带有多个ISA和PCI的插槽,该工控机可以与多种类型的控制卡和采集卡兼容。宿主计算机选用个人计算机即可,主要用于数据处理和程序调试。 试验首先将参数代入二次型或线性控制程序,运行控制程序计算所需的库仑力。随后通过式(12)计算外加电流的值。在初速度为4.3 m/s时,通过控制程序分别计算GBN、BN1、BN2控制器的最优剪切屈服力实际控制中的最优库仑力和控制电流,如表3所示。需要注意的是:本章仿真模型未考虑磁流变缓冲器摩擦力的影响,在实际控制中的最优剪切屈服力需要减去摩擦力,即 表3 实际控制中库仑力和控制电流Tab.3 The optimal yield force and control current at real case fmr_r=fmr_t-ff (24) 式中:fmr_r为实际最优剪切屈服力;fmr_t为理论最优剪切屈服力;ff为磁流变缓冲器摩擦力。 基于磁流变缓冲器的冲击防护系统控制效果,如图15所示。在最优广义宾汉数控制下,落锤在10.26 cm的行程处(稍微超出设定可用行程)速度减小至0,基本实现软着陆的目标;对于BN1控制器,控制电流较小,其输出的库仑力过小,导致落锤在13.2 cm的行程处(超过设定的可用行程3.2 cm)停止下来,无法实现软着陆的控制;对于BN2控制器,控制电流过大,其输出的阻尼力也稍大一些,落锤在8.37 cm的行程处(设定可用行程的83.7%)速度减小至0。 图15 线性宾汉数控制器与二次型广义宾汉数控制器试验结果对比Fig.15 Comparison of experimental results between linear Bingham number controller and quadratic generalized Bingham number controller (1) 基于二次型阻尼最优广义宾汉数控制策略可以实现软着陆的控制目标。而基于线性阻尼的最优宾汉数控制方法,受阻尼力模型的限制,负载会出现触底冲击或者不能完全利用完磁流变缓冲器可用行程的现象。 (2) 针对不同冲击强度(不同负载质量和初始冲击速度),最优广义宾汉数控制策略可以实现软着陆的控制目标。 (3) 在最优广义宾汉数控制策略下,系统存在唯一的最优广义宾汉数来实现软着陆的控制目标。非最优广义宾汉数将导致负载出现触底冲击或者不能完全利用完磁流变缓冲器可用行程的现象。
ΔPml45+ΔPml56+ΔPml67
1.2 试验测试

0.778 1I2+1.029 9I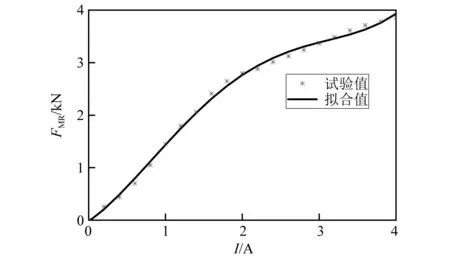

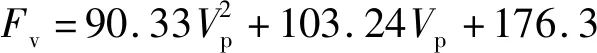
2 磁流变冲击防护系统的最优广义宾汉数控制
2.1 磁流变冲击防护系统的动力学方程
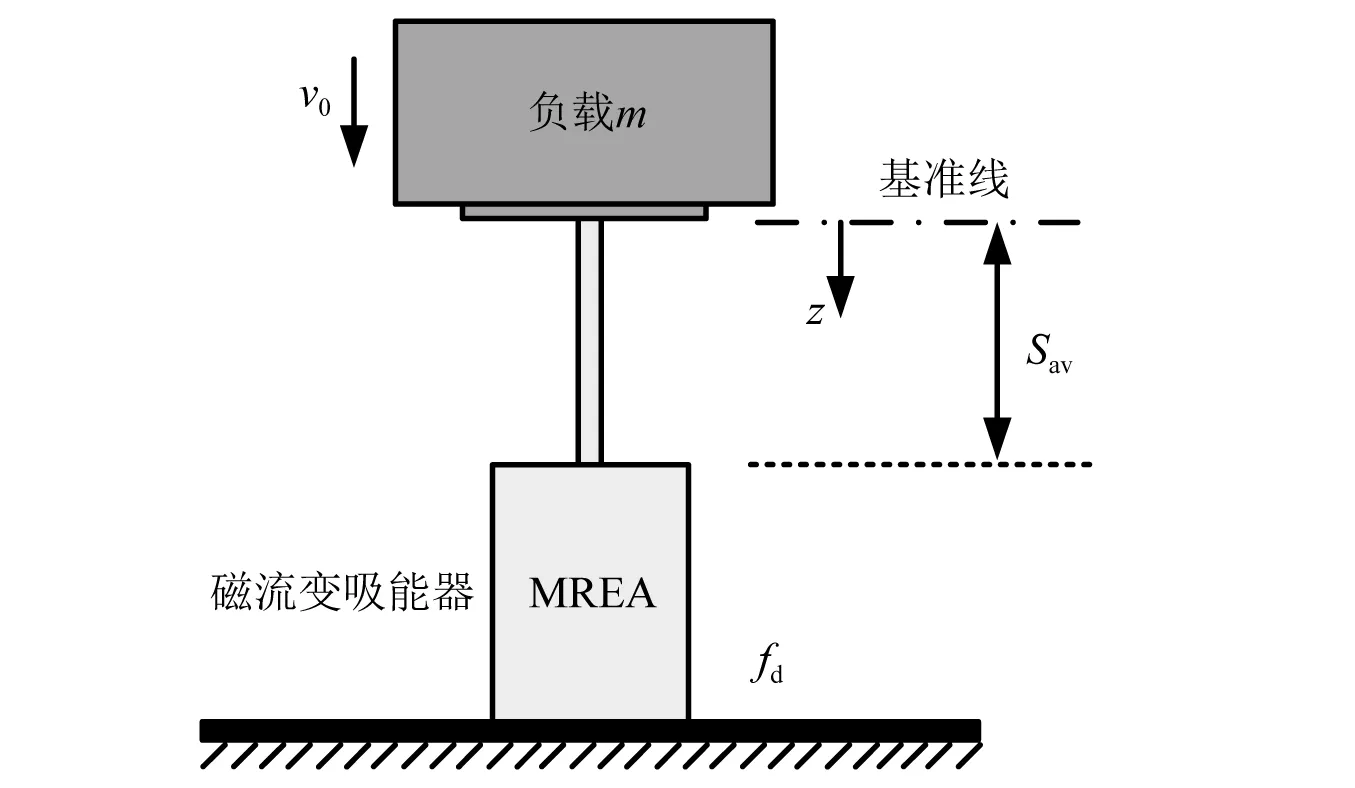
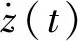
2.2 最优广义宾汉数控制
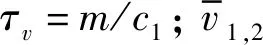
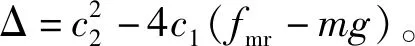
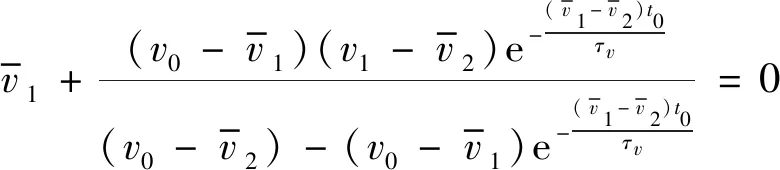
3 仿真结果

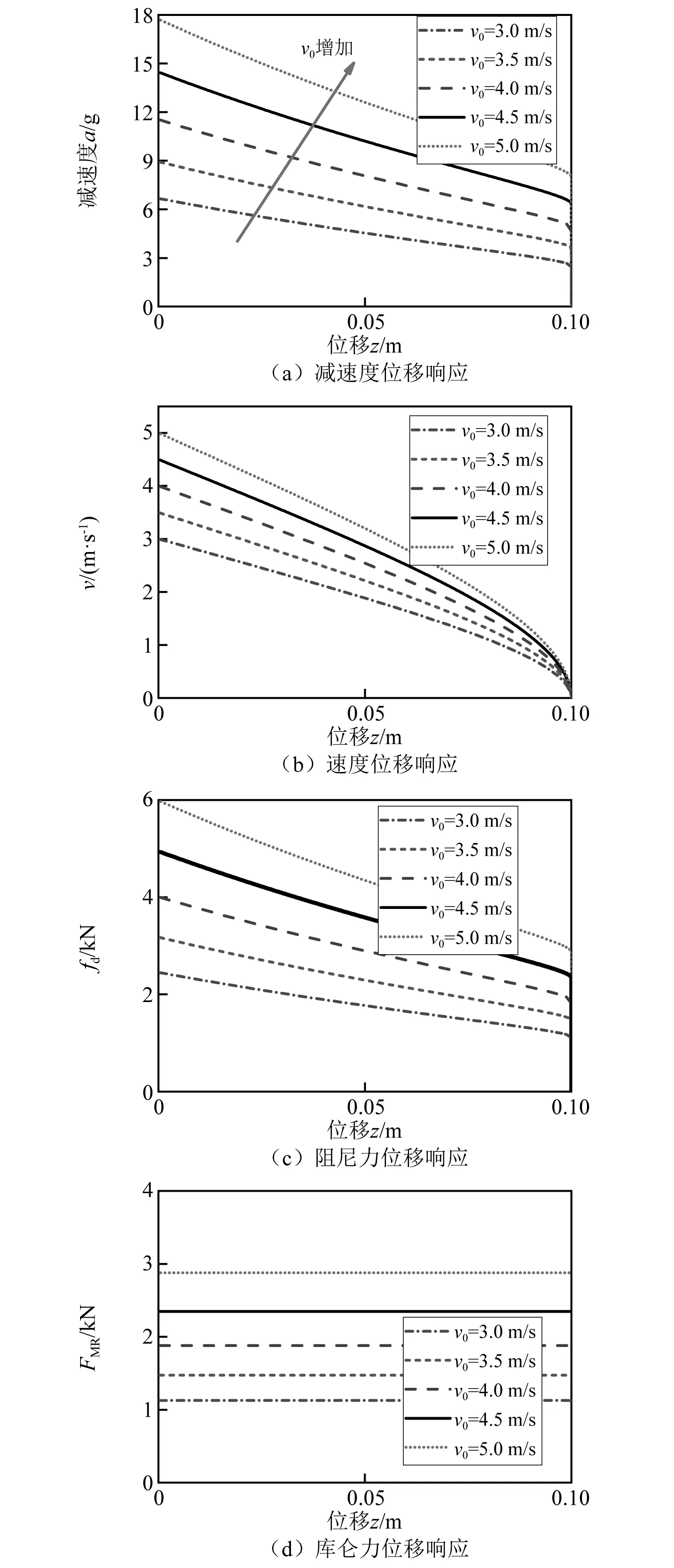
4 线性宾汉数与二次型广义宾汉数控制效果对比

5 试验研究


6 结 论

