多轴输出功率三分支齿轮系统静/动力学特性研究

宋 文，杨赪石，严 海，陈志伟，李志敏

(1.中船重工第七〇五研究所,西安 710075;2.山西省平阳重工机械有限责任公司,山西 临汾 043003)

采用功率分支技术的圆柱齿轮系统包含定轴式和周转轮系(行星轮系和差动轮系)两类。定轴式功率分支系统集成了周转轮系与普通轮系的优点，每分支的传动要求和普通齿轮传动类似，但零件数和安装要求均要低于周转轮系。同时它避免了周转轮系在高转速时离心力较大的缺点，更适用于高速传动场合，耐冲击性更强。因此，此类传动在高速重载的直升机传动[1-2]以及船舶传动系统[3]中得到了广泛的应用。

国内外学者对于功率分支齿轮系统的研究主要集中在均载性能的分析和优化方面。Krantz等[4-6]提出了一种带平衡梁的双分支齿轮系统，并对其动力学特性和均载特性进行了理论和试验研究，分析了同步角对系统均载系数的影响规律。Gmirya等[7]通过试验指出弹性扭力轴能有效改善双分支齿轮系统的均载性能。Jose等[8]分析了双分支位置角对系统均载性能的影响，并提出了实现同步啮合的解决方案。董皓等[9]、桂永方[10]、赵宁等[11]分别对功率双分流齿轮系统均载性能进行了分析，研究了不同因素对系统均载的影响规律。李楠等[12]分析了功率四分支齿轮系统的固有特性与振动特性。董皓等[13]研究了安装误差对由功率双分支闭锁轮系和行星轮系组成功率三分支系统均载特性的影响。

在鱼雷涡轮机减速器中，由于空间限制，除了主输出给螺旋桨提供动力外，许多分支上都存在额外的齿轮副啮合，将功率供给至各辅机进行工作。而现有关于功率分支齿轮系统的研究文献中，采用的对象多为单输入-单输出或多输入-单输出类型，对存在多轴输出的系统力学特性研究较少。由于额外负载的加入，导致各分支受载发生显著差别，分析此条件下系统的静/动力学特性变化，对提高系统动态可靠性设计有着重要意义。

本文采用广义有限元法，建立了鱼雷涡轮机中的多轴输出功率三分支齿轮系统的动力学模型，研究了辅机负载、齿轮安装相位、轴承参数和连接轴参数等对系统静态啮合力的影响规律，并分析了多负载时齿轮副的动态响应特点。

1 多轴输出功率三分支齿轮系统

图1为某鱼雷涡轮机中所用多轴输出三分支齿轮系统的简化示意图。动力Pin经分流级中心轮z1输入，经三个分支齿轮z2-i将功率分流，再由3个汇流级分支齿轮z3-i将功率汇流至中心轮z4经Pout1主输出。在第3分支上存在齿轮副z5-z6将部分功率传递至辅机Pout2。

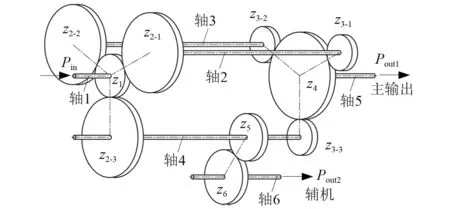
图1 单输入双输出功率三分支齿轮系统Fig.1 Tri-branching gear system with single input and double outputs

2 系统动力学建模过程

功率三分支系统存在多对齿轮副啮合，加上每个齿轮所连接的传动轴和轴承后，涉及参数较多。若采用常规集中质量法建模时，较难考虑传动轴等构件的柔性，且涉及繁琐的质量和刚度分配问题，导致结果准确性欠佳。此处采用广义有限元法对功率三分支系统进行动力学建模，能够有效解决集中质量模型中难以考虑传动轴尺寸、轴承位置等参数的问题，能更好地分析轴系与齿轮副之间的弯扭耦合特性，计算结果更为准确。

采用广义有限元法动力学建模的基本过程是：

步骤1分别将各传动轴沿轴线方向在齿轮、阶梯轴段、轴承处离散为一系列节点；

步骤2根据各节点之间的实际连接关系，将系统划分为轴段单元、啮合单元和轴承单元；

步骤3建立各单元的运动微分方程；

步骤4基于有限元法，将各单元的质量、刚度等单元矩阵进行组装，得到系统整体动力学模型。

根据图1中各构件的连接关系，可以建立系统的动力学模型如图2所示，其中bi表示第i个轴承。图中仅给出了部分轴节点示意，在实际动力学建模时轴节点的个数可根据需求以及阶梯轴段个数进行调整。

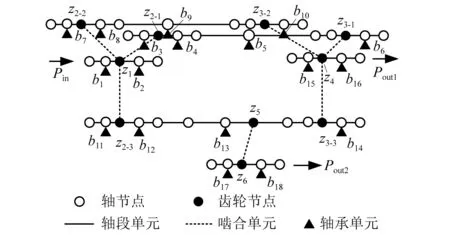
图2 功率三分支齿轮系统动力学模型简图Fig.2 Dynamic model of the tri-branching gear system

2.1 轴段单元

轴段单元采用考虑剪切效应的Timoshenko梁单元进行建模，如图3所示。定义梁单元两节点的广义坐标为qs={x1,y1,z1,θx1,θy1,θz1,x2,y2,z2,θx2,θy2,θz2}，其中：xi,yi,zi(i=1,2)为两节点沿各坐标轴的横向位移，θxi,θyi,θzi(i=1,2)为两节点各坐标轴的转角。根据文献[16]，可得到单元刚度矩阵Ks、阻尼矩阵Cs和质量矩阵Ms，则该单元的运动微分方程为

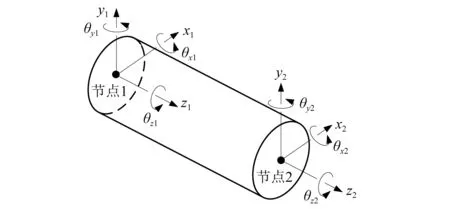
图3 Timoshenko梁单元Fig.3 Timoshenko beam element

(1)

2.2 啮合单元

图4为一对斜齿轮副考虑弯曲-扭转-轴向-摆动等各方向自由度后的动力学模型。定义主、从动轮节点的位移列向量qm= {xi,yi,zi,θxi,θyi,θzi,xj,yj,zj,θxj,θyj,θzj}T，则齿轮副沿啮合线方向的相对总变形为

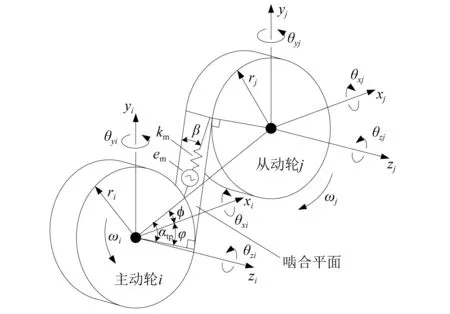
图4 啮合单元动力学模型Fig.4 Dynamic model of gear mesh element

δ=Vqm-em

(2)

式中：em为综合啮合误差，可由已知的齿面制造误差或修形通过LTCA分析得到；V为各方向位移向啮合线方向的投影向量，计算式为

V=[cosβsinφ,±cosβcosφ,∓sinβ,risinβsinφ,±risinβcosφ,±ricosβ,-cosβsinφ,∓cosβcosφ,±sinβ,rjsinβsinφ,±rjsinβcosφ,±rjcosβ]

(3)

式中：ri，rj分别为主、从动轮的基圆半径；β为基圆螺旋角，当齿轮右旋时为正，左旋时为负；各项前面的符号上半部分表示主动轮逆时针旋转，下半部分表示主动轮顺时针旋转；φ由式(4)计算

φ=αtp∓φ

(4)

式中：αtp为啮合角；φ为从动轮相对于主动轮的安装相位角。

由牛顿第二定律可以建立啮合单元的运动微分方程，整理成矩阵形式为

(5)

式中：Mm，Cm，Km分别为啮合质量矩阵、阻尼矩阵和刚度矩阵；Fm为误差激振力向量，计算式为

Mm=diag{mi,mi,mi,Ixi,Iyi,Izi,mj,mj,mj,Ixj,Iyj,Izj}

(6)

Km=kmVTV

(7)

Cm=cmVTV

(8)

Fm=kmemVT

(9)

式中：mi,mj分别为主、从动齿轮质量；Ixi,Iyi,Izi,Ixj,Iyj,Izj分别为主、从动轮绕x,y,z轴的转动惯量；km为法向综合啮合刚度；cm为啮合阻尼。

2.3 轴承单元

当忽略箱体的柔性时，轴承单元的运动微分方程为

(10)

式中：qb为轴承所在轴节点的位移列向量；刚度矩阵Kb=diag{kr,kr,kz,kθx,kθy,0}，其中，kr,kz,kθx,kθy分别为轴承径向、轴向和摆动刚度；阻尼矩阵Cb结构形式与刚度矩阵Kb相同。

2.4 系统整体动力学模型

当得到各单元矩阵和节点载荷向量后，可采用常规有限元法中整体刚度矩阵的组装方法，根据各单元节点局部编号与节点在系统整体编号的对应关系，形成系统整体质量矩阵M、阻尼矩阵C和刚度矩阵K(t)。系统整体的运动微分方程可写为

(11)

式中：X(t)为节点位移列向量；P0为系统外载荷向量，通常只包含系统所受输入和输出扭矩；Fe为误差激励载荷向量。当去掉惯性项和阻尼项后，即可得到系统的静力学平衡方程。

作者已经将该通用动力学建模流程编写了规范化的计算程序，只需在前端建模模块中建立不同构型传动系统的可视化模型后，就可生成标准化的输入数据，自动建立系统动力学方程。此方法同时模拟了齿轮、轴段、轴承等各结构柔性，可在三维空间形成节点相互连接的广义有限元动力学模型。由于许多中间参数(质量、刚度等)可自动获取，当系统构件中结构尺寸、相对安装位置或负载情况等参数改变时，只需修改非常少的参数即可进行后续分析，大大提高了模型的一致性和准确度。

3 功率三分支齿轮系统多负载力学特性

3.1 系统参数

算例功率三分支齿轮系统的参数如表1～表4所示，各齿轮、传动轴、轴承及功率点的编号与图1和图2中的编号相对应，z2和z3三个分支齿轮安装相位分别为30°，150°和270°，z6的初始安装相位取为0°。齿轮副的啮合刚度采用文献[15]中的切片法进行计算。

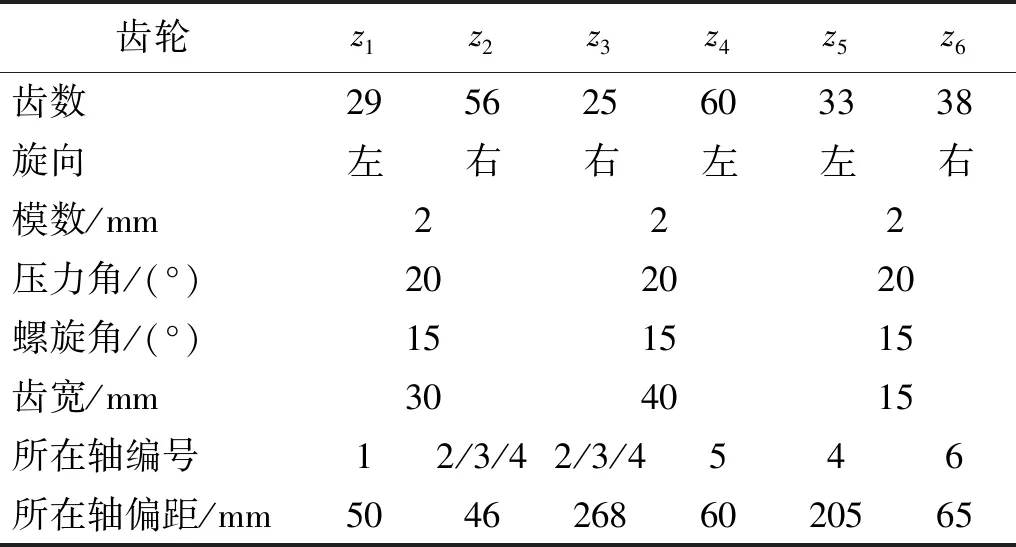
表1 齿轮副主要参数Tab.1 Parameters of the gear pairs

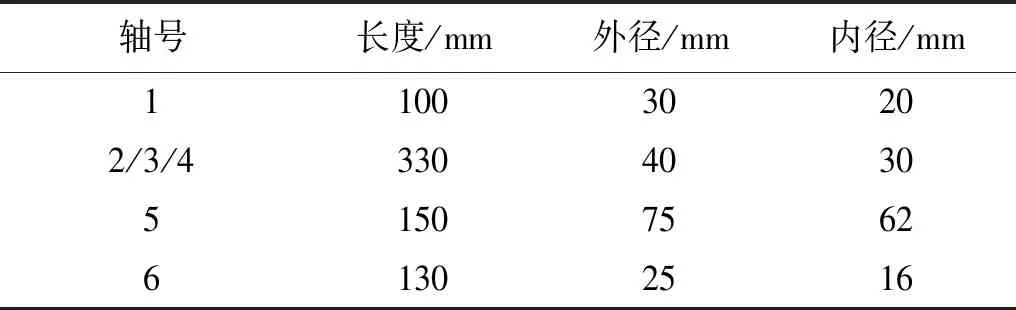
表2 传动轴参数Tab.2 Parameters of the shafts

表3 各轴承参数Tab.3 Parameters of the bearings

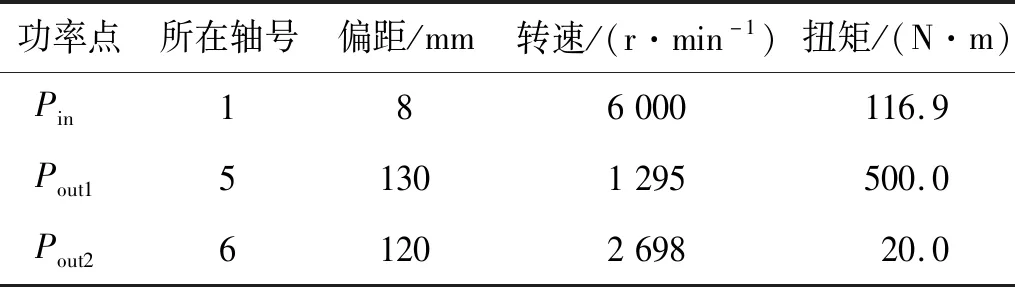
表4 各功率点参数Tab.4 Parameters of the power loads

3.2 不同因素对系统静力学特性的影响

式(11)所示的力学方程里包含了齿轮、轴和轴承等各结构的柔性，同时可计入多个系统负载，任一因素的改变都会导致系统力学特性的变化。而静力学分析下是动力学研究的基础，所以本节着重分析主要因素对系统静力学特性的影响。

3.2.1 辅机负载

表5给出了添加辅机Pout2和取消后对各齿轮副啮合力的影响。当未添加辅机时，分流级和汇流级各分支的载荷均相等，辅机所在的齿轮副z5/z6载荷为0。当在第3分支添加辅机后，对于分流级，第3分支传递的总功率增加，啮合力将增大，而另两个分支的啮合力仍相等。由于分流齿轮z1总变形增加，第1和第2分支啮合力会略有增大。而对于汇流级，第1和第2分支的啮合力相等，第3分支啮合力有所不同，但三分支的啮合力总和与未添加辅机时相同，均为8 868 N。第3分支与另两个分支啮合力的大小关系主要受连接轴、轴承和辅机齿轮相位等几个因素的影响，下面分别分析其影响规律。

表5 辅机对啮合力的影响Tab.5 Effects of auxiliary engine on the mesh forces

3.2.2 轴4结构参数

改变第3分支的连接轴4的内径，观察啮合力的变化，如表6所示。当减小轴4内径时，该分支在分流级和汇流级的啮合力都有所增加。直观上分析，当减小轴内径时，轴的扭转和弯曲刚度将增大，该分支整体刚度将增大，该分支整体变形减小，而啮合刚度大小基本不变，所以啮合力将降低。但这与计算结果是矛盾的，可以从下面的角度去分析具体原因。

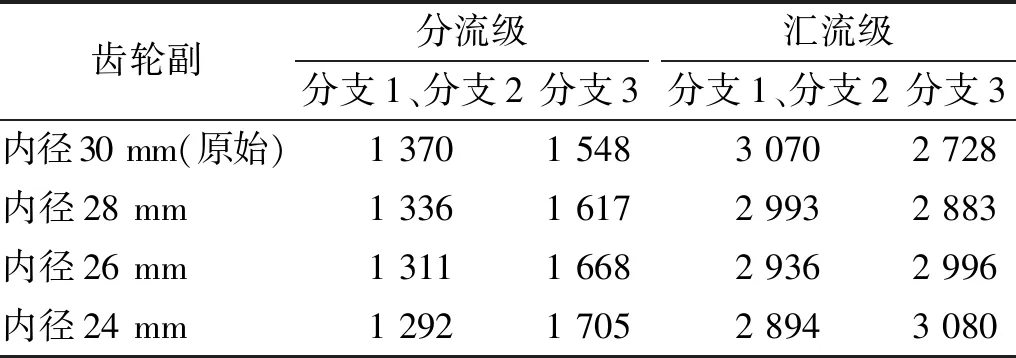
表6 连接轴4对啮合力的影响Tab.6 Effects of connecting shaft 4 on the mesh forces

取第1分支和第3分支为例，其从输入齿轮1～输出齿轮4的简化位移关系如图5所示。由于齿轮1和齿轮4的位移是一定的，所以二者之间相对位移是相等的，各分支中连接二者的构件位移矢量和应相等，即满足变形协调条件

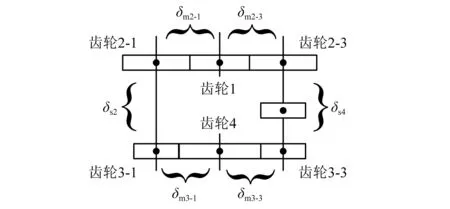
图5 级间变形简化示意图Fig.5 Schematic diagram of displacements between two stages

δm2-1+δs2+δm3-1=δm2-3+δs4+δm3-3

(12)

式中：下标mi为齿轮i啮合副变形；下标s2,s4为轴2和轴4的相对扭转和弯曲变形。当轴4内径减小时，轴刚度增大，得δs4<δs2，所以齿轮副变形δm2-3+δm3-3应大于δm2-1+δm3-1。同时，由于δs4<δs2的限制，可得分流级和汇流级的啮合变形须同时增大，即δm2-3>δm2-1，δm3-3>δm3-1。而两个分支的啮合刚度基本相等，所以可得第3分支啮合力将大于第1分支。因此，可以通过寻找合适的连接轴刚度，使汇流级各分支的啮合力实现基本相等，从而改善汇流级的均载性能。

3.2.3 轴承刚度

将第3分支汇流级轴承14各方向的刚度分别与轴承刚度比例因子做乘积，得到新的轴承刚度，计算出各齿轮副啮合力的变化，如图6所示。可以看出，当增大轴承14刚度后，第3分支的啮合力将有所增加。具体原因和连接轴的影响类似，即轴承刚度增加后，第3分支的级间连接轴4相对弯曲变形将减小，必须增加两级的啮合变形才能满足各分支变形协调条件。

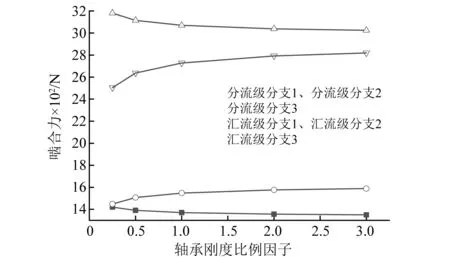
图6 轴承刚度对啮合力的影响Fig.6 Effects of bearing stiffness on the mesh forces

3.2.4 齿轮z6安装相位

改变辅机输出齿轮z6的安装相位，汇流级啮合力的变化如图7所示。由于齿轮安装相位改变后，通过齿轮z5作用在第3分支轴上的径向力方向会变化，导致汇流级三个分支上的啮合力呈周期性变化。因为该分力仅直接作用在第3分支上，所以只影响第3分支上的啮合力，另两个分支上的啮合力仍然相等。

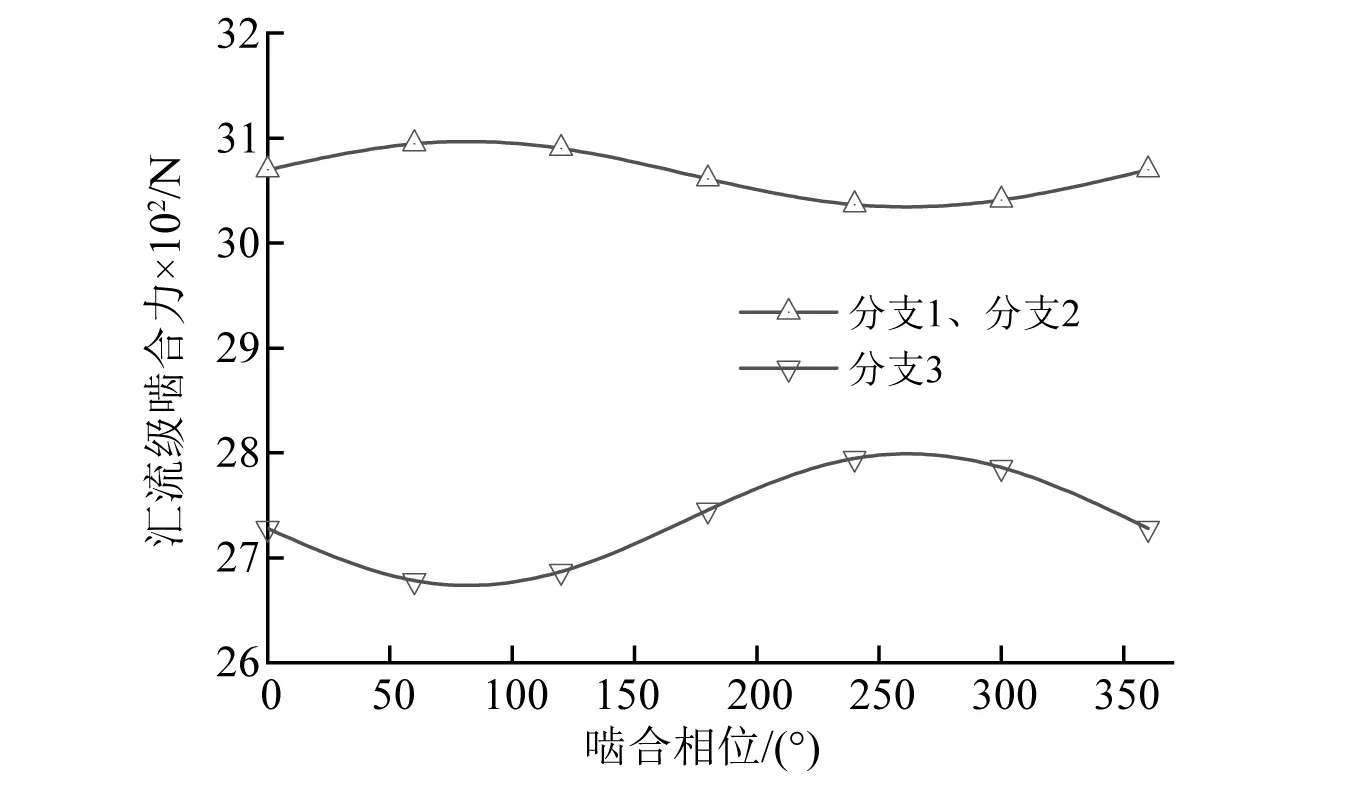
图7 齿轮6安装相位对汇流级啮合力影响Fig.7 Effects of installation phase of gear 6 on the mesh forces of power confluence stage

3.3 齿轮副动态响应规律

图8～图10给出了当输入转速为6 000 r/min时，不同齿轮副的动态传递误差(dynamic transmission error，DTE)频谱图。此时，系统共有三个啮合频率，即分流级f1=2 900 Hz，汇流级f2=1 295 Hz和辅机齿轮副f3=1 709 Hz。

对比图8(a)和图8(b)可知，分流级分支2和分支3上的DTE中，分流级频率f1及其倍频2f1所占的成分相当，且最为明显；汇流级频率f2和辅机频率f3在分支2、分支3上均有体现，可见辅机齿轮z5的振动不仅传递至z2-3，还传递至z1，影响了分支1、分支2的振动。这是齿轮z2-3所在安装轴4受到汇流级和辅机齿轮副的振动影响，会携带振动频率f2和f3，而齿轮z2-3相比z1齿数多，质量和惯量更大，其振动更容易传递至z1，导致与z1相连的其他两个分支也会出现频率为f2和f3的振动。同时还可发现，分支3上f2和f3的成分相比分支2上的更大一些，符合振动传递规律。

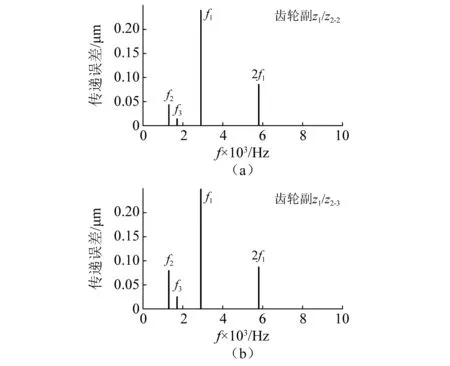
图8 分流级动态传递误差频谱Fig.8 Frequency domain DTE of power split stage

对比图9(a)和图9(b)可知，汇流级分支2、分支3的主要振动频率为自身啮合频率f2及其倍频。辅机频率f3仅在分支3上所有体现，而在分支2中的成分极小。其原因与对分流级的影响相反，即汇流级分支3上的齿轮z3-3为小齿轮，其振动对质量更大的中心轮z4影响较小，对分支1、分支2的振动影响可忽略不计。

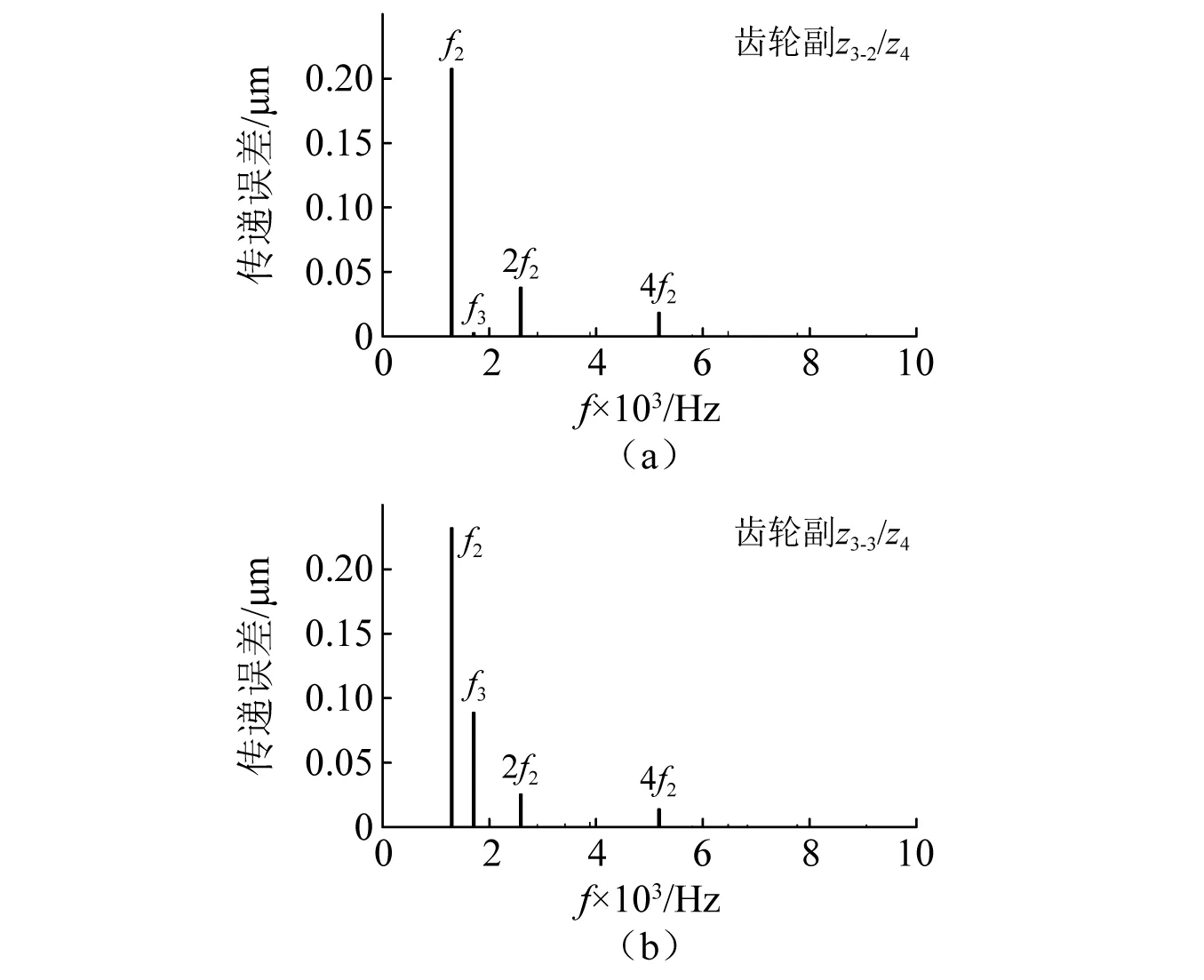
图9 汇流级动态传递误差频谱Fig.9 Frequency domain DTE of power confluence stage

观察图10可知，辅机齿轮副响应中的主要频率成分为f3和f2及它们的倍频，而分流级f1的成分基本为0。这是由于齿轮z5距离汇流级齿轮z3-3更近，且二者之间无轴承阻隔(见图2)，加之z3-3为小齿轮，在z3-3/z4齿轮副中振动更大，导致z5受汇流级的影响更明显。而分流级齿轮z2-3为大齿轮，在z1/z2-3齿轮副中振动较小，同时其与z5之间存在两个轴承阻隔，所以传递至齿轮z5的振动非常微弱。

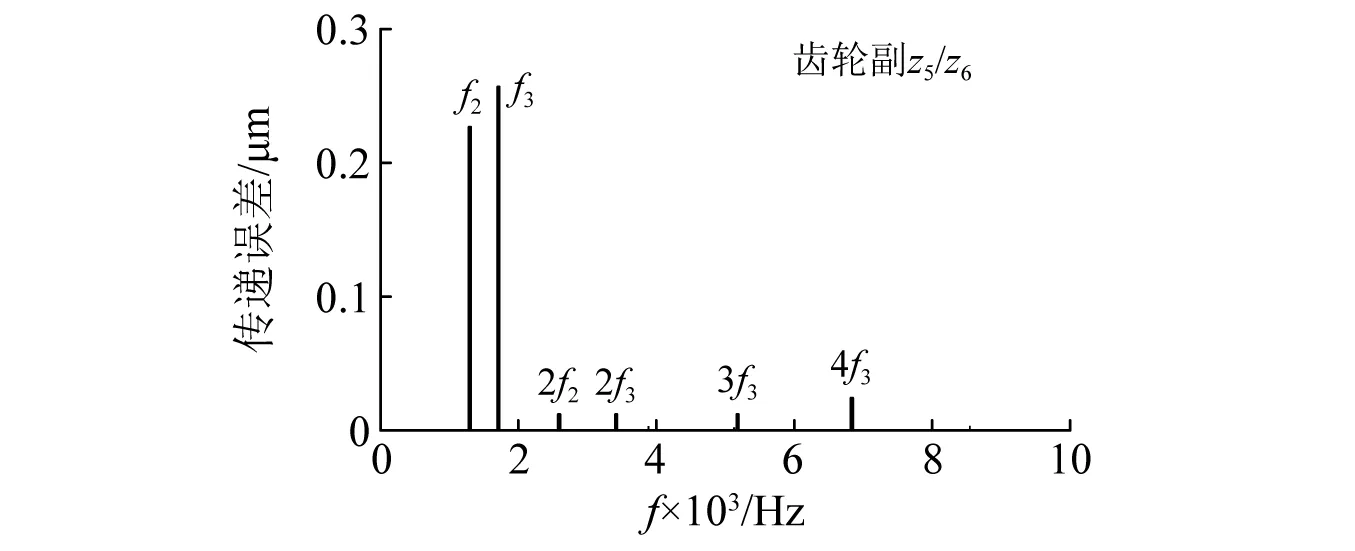
图10 辅机齿轮副动态传递误差频谱Fig.10 Frequency domain DTE of gear pair of auxiliary engine

4 结 论

本文以鱼雷涡轮机中的功率三分支齿轮系统为对象，采用广义有限元法建立了系统的动力学模型，分析了多轴输出条件下，不同参数对系统静态和动态力学特性的影响。研究的主要结论有：

(1) 在某分支添加辅机输出后，会使该分支在分流级的啮合力增大，同时导致汇流级该分支的啮合力与另两个分支产生差异。

(2) 受分支间变形协调条件的限制，当增大某分支连接轴或轴承的刚度后，会增加该分支在分流级和汇流级的啮合变形，从而使该分支的啮合力增加。

(3) 辅机齿轮副的安装相位对各分支的啮合力产生周期性的影响。

(4) 在某分支添加辅机输出后，对分流级各分支的齿轮副振动均会产生影响，而对汇流级则主要影响所在分支齿轮副的振动。

由于级间连接轴刚度对功率分支系统的影响规律已经较为明确，即减小连接轴刚度会补偿制造和安装误差，提高系统的均载性能，而本文对象为多轴输出，各分支啮合力本就不相等，所以并未分析其影响规律。在后续研究中，可进一步分析齿轮修形/误差参数、啮合错位以及不平衡力等因素对系统静/动力学特性的影响规律。