基于三维有限元的箱梁腹板剪力分配规律分析*

张 海， 臧 超， 薛兴伟

(沈阳建筑大学 交通工程学院， 沈阳 110168)

单箱多室箱梁桥在截面上存在着多道腹板，其空间力学行为复杂.研究箱梁腹板剪力分配规律，对有效确保腹板的良好工作有着重要意义和价值.李晓娅[1]对箱梁有限元模型进行数值分析，研究了箱形桥梁的抗剪性能、破坏形态及内力重分布规律，揭示了剪跨比、混凝土强度、配箍率、腹板厚度等因素对箱梁破坏形态和截面抗剪承载力的影响规律.郑辉[2]进行了箱形梁抗剪承载力试验研究，结果表明：采用等效工字梁计算箱梁的抗剪承载力是偏于不安全的.采用基于修正压力场理论的双截面法、单截面法、简化分析法、有限单元法对试验结果进行了对比分析，可得以修正压力场理论为基础的分析方法可较好地预测箱形梁的抗剪承载力.丁强[3]将各国规范抗剪计算公式进行了对比，并通过改变相关参数进行计算，分析了不同规范中在计算抗剪承载力方面的规律.

相关研究[4-11]少有单箱多室箱梁的腹板剪力分配规律方面的成果.在实际设计中进行箱梁抗剪计算时，采用各道腹板平均分担剪力的设计方法.然而，初步研究表明，受支承条件、腹板数量、腹板厚度等因素的影响，剪力在各道腹板中的分配并不能简单地采用平均分担的办法来考虑.

本文采用三维有限元分析软件，对各个条件下多个单箱多室箱梁进行计算分析，在得到的各道腹板实际分担剪力的分析和总结的基础上，得到单箱多室箱梁的腹板剪力分配规律，并给出相关的设计建议.

1 模型建立

箱梁受力相对复杂，采用常规箱梁设计理论，仅能得到典型断面特定条件下的分析结果，无法得到全桥截面的内力变化，不能体现支承条件等因素的影响.主要研究思路为：采用Midas/FEA建立多个单箱多室箱梁的三维有限元模型，利用Midas/FEA的“局部方向内力总和”提取支承条件、腹板数量、腹板厚度等不同条件下单箱多室箱梁各道腹板分担的剪力值大小，并总结得到腹板剪力的分配规律.

1.1 三维有限元模型腹板剪力提取方法

三维有限元分析模型能较好地反映结构的受力行为，但一般三维有限元分析模型的后处理中仅能输出位移和应力等结果，而弯矩和剪力等重要的内力则难以得到.研究单箱多室箱梁腹板剪力分配规律，需要提取单箱多室箱梁三维有限元分析模型各道腹板的剪力值.为了提取单箱多室箱梁三维有限元分析模型中各道腹板剪力值，采用的方法是：首先建立单箱多室箱梁的Midas/FEA三维实体有限元分析模型；然后采用Midas/FEA自带的后处理功能“局部方向内力总和”对特定截面进行内力提取.

以一单箱三室箱梁为例，提取箱梁指定截面的内力总和，主要过程为：在模型分析完成的“后处理”中，选择“后处理”中的“局部方向内力总和”，通过创建由三点构成的面(见图1a)，该面与箱梁相交(见图1b)，即完成在箱梁中截取截面.

图1 定义截面示意图Fig.1 Schematic definition of cross-section diagram

在“局部方向内力总和”功能菜单中选择截取得到的截面，点击“文本”，即输出所剖截面内力总和，如图2所示.程序输出的主要内力有：Fx(沿x方向轴力)、Fy(沿y方向剪力)、Fz(沿z方向剪力)、Mx(对x轴扭矩)、My(对y轴弯矩)、Mz(对z轴弯矩)，同时给出了中性轴位置.

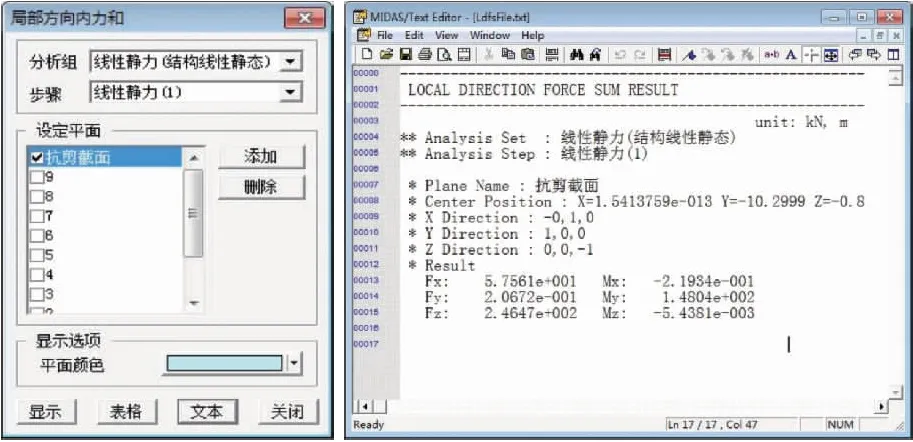
图2 局部方向内力总和计算Fig.2 Calculation for sum of internal forces in local direction

研究腹板剪力分配规律需要提取各道腹板的剪力，提取腹板剪力时，需要在进行内力总和计算之前，仅激活待提取剪力腹板的单元，在随后的内力总和中，所得到的结果即为仅激活腹板部分单元的内力总和.

1.2 腹板剪力分配规律研究模型

本文主要对支承条件(箱梁支座截面的支座数量)、腹板数量、腹板厚度等条件下单箱多室箱梁各道腹板分担的剪力值大小进行提取，并总结得到腹板剪力的分配规律.

基本的箱梁参数为：跨径25 m，梁高1.60 m，顶板、底板厚20 cm.跨中标准段长10 m，腹板变宽段长2.5 m，腹板加宽段长3.8 m，端横梁长1.2 m.支承条件、腹板厚度及腹板数量为研究变化参数.各个条件下的分析模型介绍如下.

1) 不同支承条件下腹板剪力分配规律研究模型.箱梁为宽20.4 m、底宽15.4 m的单箱五室箱梁，箱室间距300 cm.腹板厚度由40 cm线性渐变为60 cm.该条件下箱梁支承的类型有：模型Ⅰ，双支座，支座间距14.2 m，如图3a所示(单位：cm)；模型Ⅱ，三支座，支座间距7.1 m，如图3b所示(单位：cm)；模型Ⅲ，四支座，支座间距4.7 m，如图3c所示(单位：cm).

图3 支座间距Fig.3 Support spacing

2) 不同腹板数量条件下腹板剪力分配规律研究模型.箱梁为宽20.4 m、底宽15.4 m的单箱五室箱梁，腹板厚度由40 cm线性渐变为60 cm，采用支座间距为14.2 m的双支座.分别采用单箱双室(三道腹板，腹板间距740 cm，模型Ⅳ)、单箱三室(四道腹板，腹板间距483 cm，模型Ⅴ)、单箱四室(五道腹板，腹板间距385 cm，模型Ⅵ)和单箱五室(六道腹板，腹板间距300 cm，模型Ⅶ)四种模型进行对比分析.

3) 不同腹板厚度条件下腹板剪力分配规律研究模型.在模型Ⅵ基础上，采用支座间距7.1 m的三支座形式，对腹板厚度进行改变，共有4种分析对比模型：腹板厚度35～55 cm(模型Ⅷ)、腹板厚度40～60 cm(模型Ⅸ)、腹板厚度45～65 cm(模型Ⅹ)、腹板厚度50～70 cm(模型Ⅺ).

2 箱梁剪力分配规律

对各道腹板截面名称进行约定，以单箱五室为例(见图4)，约定最外两个腹板为边腹板，向截面中心方向依次为次边腹板和中腹板.

图4 跨中断面腹板名称Fig.4 Naming of mid-span cross-section webs

腹板截面为在自重和二期恒载作用下，在纵桥向以跨中为零点，向支座以间距(1.3+18×1.0+1.3) m截取20个截面分析断面，用以考查各道腹板剪力在纵桥向上的分配规律，模型截面选取如图5所示(单位：cm).

图5 模型截面选取Fig.5 Selection of model cross-section

2.1 不同支承条件下腹板剪力分配规律

模型Ⅰ、模型Ⅱ和模型Ⅲ为不同支座间距的分析模型，箱梁为宽20.4 m、底宽15.4 m的单箱五室箱梁，箱室间距300 cm.

按常规设计方法可知，Va=Vt/Nf，其中，Va为每道腹板平均分配的理论剪力值，Vt为全截面剪力值，Nf为腹板的道数.

按照图5选取截面，分别提取模型Ⅰ、模型Ⅱ和模型Ⅲ的边腹板、次边腹板和中腹板所分担剪力及全截面剪力值，各模型各道腹板的剪力值在纵桥向上的变化曲线如图6所示.由图6可知，边腹板所分配的剪力值较次边腹板及中腹板都大，而非均匀分配.

图6 不同支承条件下腹板剪力分配与剪力增大系数Fig.6 Shear force distribution and increasing coefficient of webs under different supporting conditions

将各道腹板的剪力值Vi除以单道腹板平均分配的理论剪力值Va，得到各道腹板Vi与Va的增大系数η(η=Vi/Va)，图6中“平均值”曲线表示η=1.0，由图6可以看出，箱梁腹板分担剪力并非平均分配，其中边腹板的剪力增大系数η大于1.0，偏不安全；次边腹板及中腹板的剪力增大系数η小于1.0.模型Ⅰ边腹板的剪力增大系数η，在跨中为1.58，在支点截面为1.64，较均值1.0而言，增大倍数较大.另外，模型Ⅱ和模型Ⅲ边腹板的剪力增大系数η在支点截面分别为1.31、1.27，设计中亦不能忽视.

双支座情况下各道腹板分配的剪力值差别最大，这是因为在支点附近，支座所支承腹板直接承担了支座的反力，因此，支座所支承腹板的剪力值在支点附近也最大.根据圣维南原理，在向跨中延伸的方向上，各道板分担的剪力值在数值上逐渐接近平均分配的理论值，且各道腹板剪力值差距逐渐减小.

2.2 不同腹板数量下腹板剪力分配规律

模型Ⅳ、模型Ⅴ、模型Ⅵ和模型Ⅶ为不同腹板数量的分析模型，箱梁为宽20.4 m、底宽15.4 m的单箱多室箱梁，采用间距为14.2 m的双支座形式，且分别对应腹板间距740 cm的单箱双室、腹板间距483 cm的单箱三室、腹板间距385 cm的单箱四室和腹板间距300 cm的单箱五室模型.

经分析，模型Ⅳ～Ⅶ的边腹板剪力增大系数η均大于1.0，次边腹板及中腹板的剪力增大系数η小于1.0，为节省篇幅，本文仅给出模型Ⅳ～Ⅶ剪力增大系数大于1.0的边腹板计算结果，如图7所示.

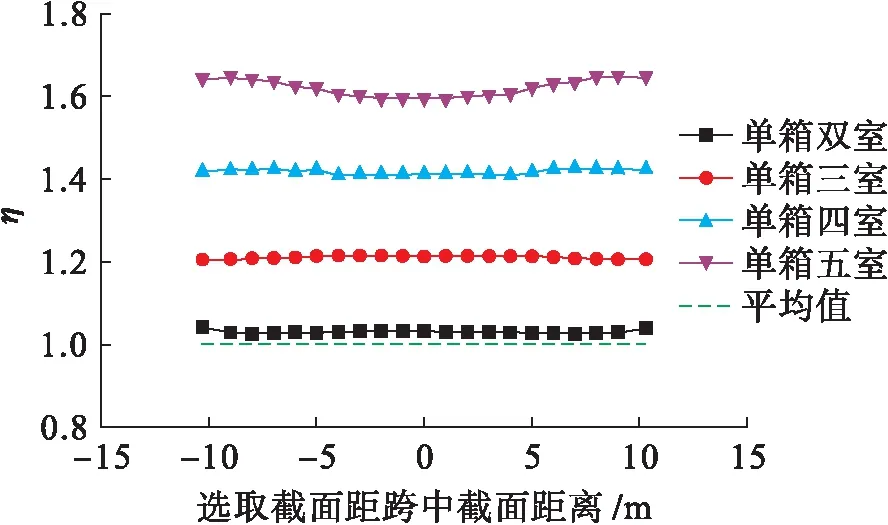
图7 不同腹板数量下边腹板剪力增大系数Fig.7 Increasing coefficient of shear force of side webs under different web number

由图7可以看出，在支承条件不变的条件下，随着腹板数量增加，腹板的剪力增大系数η依次增大，以支点截面为例，模型Ⅳ、模型Ⅴ、模型Ⅵ、模型Ⅶ中η分别为1.04、1.21、1.42、1.64.

2.3 不同腹板厚度下腹板剪力分配规律

模型Ⅷ、模型Ⅸ、模型Ⅹ和模型Ⅺ为不同腹板厚度的分析模型，箱梁为宽20.4 m、底宽15.4 m的单箱四室箱梁，支座间距为7.1 m，分别采用腹板厚度35～55 cm、腹板厚度40～60 cm、腹板厚度45～65 cm、腹板厚度50～70 cm.

剪力分配结果为边腹板分配剪力最大，且各个模型边腹板的剪力增大系数η均大于1.0.将各个模型边腹板的剪力增大系数η进行对比分析，结果如图8所示.由图8可以看出，跨中腹板厚度由35 cm变化至50 cm，模型Ⅷ、模型Ⅸ、模型Ⅹ和模型Ⅺ的剪力增大系数η相差不到1%，说明腹板厚度对腹板剪力分配影响不大.

图8 不同腹板厚度下边腹板剪力增大系数Fig.8 Increasing coefficient of shear force of side webs under different web thickness

3 剪力分配规律设计对策

通过上述多个单箱多室箱梁模型计算结果对比分析可知，单箱多室箱梁的腹板剪力分配受支承条件、腹板数量影响较大；边腹板所分担的剪力值较次边腹板及中腹板大.因此，将全截面剪力平均分配到各道腹板进行设计计算，对边腹板是偏于不安全的.

由《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2012)中斜截面抗剪承载力公式可知，箱梁腹板的抗剪承载力受腹板厚度的影响较大，因此可以得出结论：在进行抗剪设计时，可适当增加边腹板厚度，减薄次边腹板及中腹板的厚度，从而提高箱梁的抗剪承载力.针对箱梁边腹板承担较多剪力的受力特性，结合腹板厚度对剪力增大系数η影响小的特点，本文提出依据剪力增大系数η计算结果加厚边腹板、适当减薄次边腹板和中腹板的设计理念，以达到腹板的抗剪能力与承担的剪力大小相互匹配、各道腹板同时达到抗剪承载力的目的.

现以模型Ⅵ单箱四室箱梁为例，原设计方案为支座间距7.1 m的三支座，边腹板厚度为40 cm渐变至60 cm，边腹板最大剪力增大系数η为1.19，次边腹板和中腹板最大剪力增大系数η分别为0.83和0.97.根据剪力增大系数η计算结果，将边腹板厚度进行调整，即40×η=47.6 cm，60×η=71.4 cm，依据该计算结果，将方案取整调整为50 cm渐变至70 cm；由于次边腹板和中腹板最大剪力增大系数η为0.97，所以不做腹板厚度的调整.

再次对优化设计后的方案进行剪力增大系数η提取，得到边腹板最大剪力增大系数η为1.24，与边腹板厚度为原方案平均厚度的1.25倍相匹配.次边腹板和中腹板最大剪力增大系数η分别为0.80和0.93，与原设计方案平均厚度的1.0倍基本匹配，偏于安全.

4 结 论

本文对不同支承条件、腹板数量、腹板厚度等条件下单箱多室箱梁腹板的腹板剪力分配规律进行了研究，得到如下结论.

1) 在不同支承条件、腹板数量、腹板厚度等条件下，单箱多室箱梁腹板剪力的主要分配规律为：

① 不同支承条件对剪力增大系数η影响较大，其中双支座剪力增大系数η最大，在跨中为1.58，在支点截面为1.64，较均值1.0而言，增大倍数较大.

② 在支承条件不变的情况下，腹板数较少时，边腹板与中腹板(次边腹板)剪力增大系数η差别小；边腹板的剪力增大系数η大于1.0，并随着腹板数量增加，逐渐增大.

③ 腹板厚度变化对剪力分配影响不大.对于单箱多室箱梁，其腹板分担剪力并非平均分配，不同支承条件、腹板数量、腹板厚度等条件下，边腹板所承担的剪力值均大于平均值，按照常规设计偏危险.因此，设计中应通过可靠的方法计算得到腹板剪力增大系数η后，进行合理设计.

2) 提出了腹板剪力增大系数η的概念，并提出按照腹板剪力增大系数η的计算结果调整腹板厚度的方法，可基本实现腹板同时达到抗剪承载力，有效防止边腹板提前破坏.