基于培养学生创新意识的数学课堂教学

查艺

摘  要：培养学生的创新意识，提高创新能力，是新教育改革的重要内容之一，也是每个教师应该面对与思考的课题。创新意识是形成创新思维的基础，创新思维又是形成创新能力的灵魂。文章从教师如何引导学生从观察、互动、表征和实践操作四个方面迸发创新意识，提升创新能力进行粗浅的阐述。

关键词：创新意识;观察;互动;多元表征

创新意识指的是人们根据个体或社会的发展需要，创造之前从未有过的观念或事物的设想、意向与愿望，它是人类创造活动的内在动力和出发点的积极表现形式。培养小学生的创新意识，是推动祖国未来发展的重要措施之一。数学作为小学里的主要学科，自然是培养学生创新意识的主要阵地。因此，教师应在思想上、行动上重视创新意识的培养，从课堂教学的各个层面渗透创新意识、拓展学生的创新思维，提高创新能力。

一、从敏锐的观察中培养创新意识

聪慧的大脑，都离不开一双善于发现的眼睛。学生在观察事物的过程中，会将事物与自己已有的知识联系到一起思考，比较两者之间的异同点，找出事物的内部联系，自然地做出新的思考 [1]。教师可在日常教学中有意识地引导学生观察题目，感受其中的规律与联系，产生新的思考。

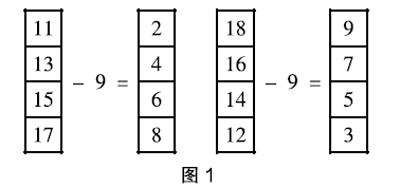
例1：以“十几减9”这道题为例：

教师让学生先不着急答题，而是观察此题，寻找题中存在的规律，根据这个规律寻找简便答题的方法。学生通过观察发现第一题中纵向的被减数是相邻的奇数，第二题中纵向的被减数是相邻的偶数。发现这个规律后让学生将答案填写在空格里，完成后要求学生再次观察这两道题。学生得出以下结论：单数-9=双数，双数-9=单数;被减数越大，结果越大，反之，被减数越小，结果越小;每个得数都是“被减数的个位数+1”。一个学生还惊讶地发现，不管是十几-9，结果都等于被减数的个位数和十位数相加，比如，15-9=1+5=6，12-9=1+2=3……如此类推。大家都为这个发现而兴奋不已，原来看似简单的一道题，竟然还存在着如此神奇的规律。学生的学习兴趣被完全调动起来后，不少学生主动地尝试减数为其他数，这个规律是否合适;被减数是一位数或三位数是否适用这个规律，等等。

由此可见，融洽的课堂氛围和细致的观察，能激发学生的学习兴趣，启发学生发现事物内部的联系，通过对比、思考和求证，产生创新思维。

二、在积极的互动中培养创新意识

“亲其师”才能“信其道”。课堂是师生、生生之间互动交流的主要阵地，教师需将情感与知识融合，感召学生产生以求知欲为主的需要结构。2011年版的新课标明确提出：“教师在课堂教学中，要处理好授课和学习的关系，鼓励学生通过合作交流、主动探索，逐渐产生创新意识。”因此，让学生主动地参与到“教”中来，让思维“动”起来，让创新意识“活”起来是课堂教学的主要方向。

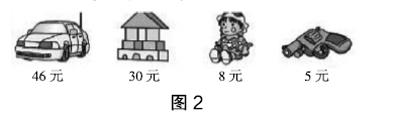
例2：观察图2，提出不同的问题。

师：观察图2，想想你能提出哪些问题。

生1：布娃娃比玩具手枪贵几元？

生2：积木比玩具汽车便宜几元？

师：非常好，你们都是出题高手。其他同学想想还能提出怎样的问题呢？

生3：布娃娃比积木便宜几元，比玩具手枪贵几元？

师：不错，这位同学也是一个出题高手。同学们数数他提出了几个问题？

生（齐回答）：2个。

生1：我又想到了一个更难的问题：买四样物品一共需要多少元？

学生对这个问题很感兴趣，很快算出需要89元。

生4：如果都用10元一张的人民币支付，至少需要几张人民币？

生（齐答）：9张。

生5：如果都用5元一张的人民币支付，至少需要几张人民币？

此时，热闹的教室瞬间安静了下来。

师：这是一个有挑战性的问题，有没有同学能回答？

生3：应该少于20张（不确定地说）。

师：100里面有20个5，那90里面有多少个5？

生5：20个5组成100，那90就是少两个5，买这四样玩具至少需要18张5元。

师：非常好，大家开动小脑筋想想还有什么方法可以得出答案呢？

生6：9张10元人民币摆一排的话，那5元人民币就是摆放成两排，也就是18张。

教师把生6的思路用图形板书到黑板上，学生瞬间都豁然开朗了。一道简单的数学题，通过问与答的展开，由简单到复杂层层递进，见证了学生的思考过程和创新历程。

课堂是师生、生生互动、交流的平台，只要用心捕捉学生的闪光点，给予积极的鼓励与引导，就能激发学生以求知欲为主的需要结构，课堂交流也就能成为创新意识的发源地。

三、从多元表征中培养创新意识

多元表征是指对同一个数学对象，使用数（数字、文字、式子等）或形（几何图形、数学模型或图像等）多种形式进行表征。多元表征能帮助学生对数学知识进行转换与联系，加深理解，构建更完善的认知结构，启发学生产生创新意识 [2]。

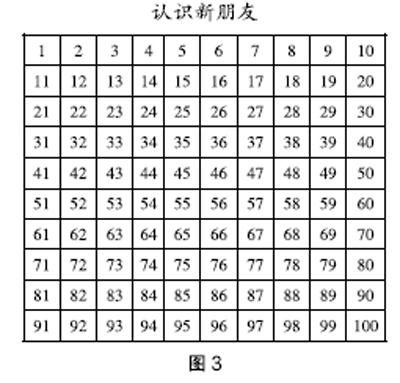
例3：观察“认识新朋友”这张百数表（图3），寻找规律。

认识新朋友

师：同学们，观察这张百数表，找找这张表里的数字有什么规律，可以横着看或竖着看。

生：竖着看每列里的十位数，下面一个数总比上面一个数大1。

师：十位数上的1表示一个10，从上往下看，下面一个数比上面一个数多多少？反过来，上面的数比下面的数少多少？

生：下面的數比上面的数依次多10，上面的数比下面的数依次少10。

师：表达准确，大家再横向看看有什么规律呢？

生：我发现从左到右，每个数依次加1，从右往左，每个数依次减少1。

师：同学们观察得非常仔细，这么快就准确地找出了其中的规律。现在老师将横向相邻两个数的关系用线段来表示（见图4），你们还有其他的表示方法吗？