问题引领思维,促发“深度”学习
邱苏敏
摘 要:问题是推动和引领学生深度思考、主动探究的基础。文章在分析问题解决与深度学习的内涵意义的基础上,探讨了基于问题解决的小学数学深度学习策略。认为教学中教师要强化问题意识,发挥数学问题对思维的引领作用,引领学生在有效的数学探究活动中促进思维不断深入推进,促发“深度”学习。
关键词:小学数学;问题解决;深度学习;思维
问题是推动和引领学生深度思考、主动探究的基础,能促使学生在有效的探究中诞生新的思想和方法,提升学生的问题解决和思维能力。然而,目前小学数学教学止于知识性教学,数学教学缺乏应有的深度,学生的学习活动还停留在较浅的层面,思维得不到有效的发展,问题自然也得不到真正的解决,一旦情境發生变化,学生对问题的解决就容易出现不知所措的现象。这种现状需要教师强化问题意识,借助问题的驱动效应,引领学生的思维不断深入推进,引领学生独立走在自主建构的路上。
一、理论建构:问题解决与深度学习
基于问题解决的深度学习策略探寻,首先需要从理论层面对“问题解决”和“深度学习”进行建构,从而使问题得到真正解决,深度学习得以真正发生。
1. 问题解决
目前,基于问题解决的理论研究取得了较大的成果,丁念金教授出版了《问题教学》一书,对“问题解决”进行了系统性的论述;此外,外国理论研究者杜威也就“问题解决”进行了研究。综合当前“问题解决”理论研究成果,一般认为“问题解决”以问题为中心、以自主学习和探究学习为主要方式,引领学生在解决问题的过程中,获得知识,提高解决问题的技能,并不断提高学生数学思维品质 [1]。问题解决的中心是问题,它是数学课堂知识、技能、思维等发展的载体,内核是学生,以培养学生解决问题的能力作为最终的价值导向。
2. 深度学习
我国学者黎加厚教授、安富海教授等,对“深度学习”进行了深入的研究,深度学习是相对于浅层学习而言,它以理解为基础,以高阶思维为支持,学生在深度学习的过程中,不是被动地接受,而是对所学习的内容持有批判性的态度,在批判接受的过程中形成新的知识和思想,并与既有的知识和思想等进行结构化的对接。深度学习获得的知识、技能、方法和思想等,具有普遍的适应性,能够指导学生解决新场景、新情境下的问题。
二、策略与实践:基于问题解决的小学数学深度学习
基于问题解决的小学数学深度学习的策略,必须保持与数学教学内容、教学环节的高度的匹配度,从而提高策略的可操作性。
1. 精心设计问题,明确价值指向
问题是问题解决和深度学习行为发生的前提和基础,只有设计出高价值密度的问题,并注重问题之间的关联性,才能明确问题解决和深度学习的价值取向。问题要发挥对思维引领的作用,需要关注以下几个重点:
(1)紧扣知识。问题设计要紧紧围绕本课教学内容,能够将知识有机地渗透在问题中,从而使问题成为数学教学的载体,并借助问题引领学生深度学习发生,提高学生运用知识解决问题的实际能力。
(2)形成结构。问题解决和深度学习,不是单纯的、碎片化知识的传授和习得,需要学生在既有知识的基础上,通过问题解决和深度学习,使新旧知识、方法等,形成系统的结构,因此问题的设计要形成问题链条,教学程序要形成有机的板块,从而发挥问题的驱动作用。
以苏教版五年级“折线统计图”为例,本课的教学任务包括认识简单的折线统计图(含其结构、特征),能够绘制简单的折线统计图去解决实际问题。因此,问题的设计要紧扣这些知识点,并基于知识之间的关联性,设计出互为观照的问题和科学的教学板块,引领学生从浅层的读析折线统计图,深入到绘制折线统计图,并能够基于新的场景运用折线统计图解决问题。
2. 创设问题情境,激发探究情绪
问题呈现方式直接关系着问题效应,也关系着学生的学习是否具有意义,是否能够对问题解决和深度学习产生直接或者间接的驱动意义。这就需要我们给问题这匹“好马”配上“好鞍”,通过创设问题情境,激发学生在问题解决和深度学习时拥有积极情绪。
问题情境如何创设?首先需要指向情境创设的本质,聚焦问题解决的本质。因此,我们在创设问题情境时,要精准把握问题设计的意图,从而根据问题设计的意图,利用情境的直观性和感染性,引领学生紧紧逼近问题解决的目的。此外,问题情境的设计,要注重激荡性,不宜平铺直叙,适宜使问题情境体现出一定的挑战性,可以借助新旧认知冲突,也可以是前概念认知冲突等,能够真正发挥问题的驱动效应。
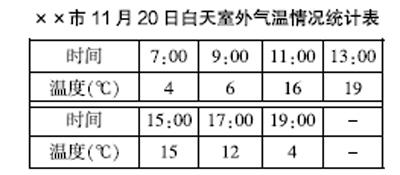
以“折线统计图”导入为例,在导入环节,笔者设计了这样一个问题情境:小明非常热爱气象,下面是他根据11月20日白天室外气温情况,测量绘制的一种统计表,说一说你从统计表中获得了哪些信息。
××市11月20日白天室外气温情况统计表
除了运用统计表进行数据统计外,你还有没有其他统计的方法?
这个环节,利用小明的一份统计表创设问题情境,引导学生形成“统计”意识,唤醒学生统计学知识;在此基础上,又引发新的问题,引导学生的思维进行扩散,学生很快想到利用“条形统计图”,这样学生的思维就从“统计表”向“条形统计图”延伸,促进新旧知识的融合;在此基础上,教师再引出“折线统计图”,就显得自然而然,学生深度探究的情绪也不断活跃了起来。
3. 关注自主体验,促进深度理解
建构主义认为,学习是学生自主建构的过程。这就需要小学数学问题解决的过程中,能够关注学生的自主体验,并让学生充分地体验,能从单一化的体验走向多样化的体验,在深度体验中达到深度理解的目的。
充分地体验,需要教师改变“填鸭式”问题解决方式,给予学生足够的时间、机会,利用自身的知识、经验、方法等自主体验,在学生自主建构的基础上,再给学生创造走进“小组”的机会,让学生之间进行互动,丰富学生的体验。体验不能过于单调,要基于问题解决和知识的结构化,让学生的体验从单一化、浅层次、简单化走向多样化、深层次、综合性,让学生的手、眼、脑、嘴、耳等都动起来。
“折线统计图”的体验环节,设计了以下几个板块:
看一看:仔细观察教材中的折线统计图,看一看它是怎样组成的?有什么特征?
想一想:根据你所观察到的折线统计图,根据它的结构和特征,你能不能给它下一个定义,与同桌交流。
辨一辨:将小明绘制的统计表、条形统计图和折线统计图等放在一起,比較一下,各自有哪些特点,你认为它们的存在是否重复多余,说出你的理由。
这个环节,立足于学生自主体验,先引导学生进行观察,从而从外再把握折线统计图的组成和特征;第二环节,促使学生从感性认识到理性认识,借助形象思维媒介,引导学生进行理性转变,通过下定义促进学生对“折线统计图”的深度理解;最后,通过辨析统计表、条形统计图和折线统计图,帮助学生在三者之间初步建立起关联性,从而为认知结构的同化进行铺垫。
4. 深度整合加工,同化认知结构
数学学习的过程是信息获取的一个过程,学生初期获得的信息是零碎的、片面的,是浅显的。如何引导学生将获得的信息进行深度整合加工,这是深度学习必然要经历的一个过程,也是学生解决问题所不可或缺的一个过程。深度整合和加工离不开归纳和同化,归纳的方法很多,可以借助比较手段,同化的路径则相对固化,即借助场景重构,在问题解决的实际应用过程中使认知结构得以同化。
“折线统计图”一课,归纳环节,笔者主要引导学生围绕“统计”大主题,对统计表、条形统计图、折线统计图进行比较,设计了这样探究问题:根据所学的知识,你能不能围绕结构、特征、优势等三个维度,利用思维导图的形式,对统计表、条形统计图、折线统计图进行比较归纳。
这个环节,以问题引领学生的思维,并对学生的归纳给予指导,即对学生比较的方向给予提示,从而降低学生归纳的难度,提高归纳的有效性;同时,运用思维导图的方式要求学生进行比较归纳,又让学生掌握归纳总结的一种常见方法,从而使思维导图引领学生的思维向高阶升级。
同化环节,笔者设计了三个统计场景,让学生根据所提供的应用场景,从统计表、条形统计图和折线统计图等三种统计方法中选择合适的统计方式。由于重构了问题解决的情境,并基于三种统计方式,扩大了问题解决的场景,从而真正实现学生知识结构的同化,强化学生统计思维和思想的发展 [2]。
总之,问题解决理应成为小学数学教学的基本价值取向。小学数学教师要基于问题解决的深度学习需求,进一步提高自身理论素养,并将理论付诸实践,在数学教学实践中不断探索基于问题解决的深度学习策略,从而引领学生自主走在深度学习的路上,使学生问题解决的能力得到真正的发展。
参考文献:
[1] 江志杰. 创造性挖掘教材 针对性提升素养——“椭圆标准方程的应用:教学札记[J]. 中学教研(数学),2019(02).
[2] 宋慧娴,刘荣. 小学数学基于问题解决的深度学习模式探索[J]. 小学数学教育,2016(17).

