巧用数学归纳法解数列竞赛题

徐 冲 顾晓峰

(江苏省锡山高级中学，214174)

近期,笔者通过阅读与尝试解答各地区数学竞赛模拟题中的数列题,发现诸多题目均可用数学归纳法解决．本文通过几道例题不同解法的比较，感受数学归纳法在解决有关正整数命题中的优势.

一、知识准备

一般地,证明与自然数有关的命题p(n)，中学教材主要介绍的是第一数学归纳法，其理论依据(也是解题步骤)如下.

第一数学归纳法

(1)证明当取第一个值n0时命题p(n0)成立；

(2)假设当n=k(k≥n0,k∈Z)时命题p(n)成立,证明当n=k+1时命题p(n+1)也成立.

综合(1)(2),可得对一切自然数n≥n0，命题p(n)均成立.

除此之外，使用较频繁的还有第二数学归纳法.

第二数学归纳法

(1)证明当n=1,2时命题p(n)成立；

(2) 假设当n≤k时命题p(n)均成立,证明n=k+1时命题p(n+1)也成立.

综合(1)(2)，可得命题p(n)对一切自然数n均成立.

二、应用举例

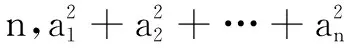
证明当n=1时，可取a1=5.

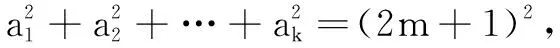
由归纳法原理知满足条件的数列存在.

评注此题直接使用第一数学归纳法,构造和递推的过程同时进行，难点是ak+1的构造．

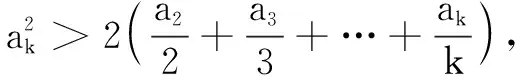
此时我们需要对题目所要证明的结论适当加强，改为证明

(*)

证明当n=2时，(*)式成立.

综上，命题得证.

评注此题也可使用综合法证明，读者可以尝试.

证法1当n=1时，a1≥a1，不等式显然成立.

综上，可知原命题成立.

评注此题尝试第一数学归纳法无法证明，使用第二数学归纳法证明时，相对于第一数学归纳法，假设中提供的条件更多，更有利于归纳过渡.此题也可用以下的构造方法证明，读者可以比较两者的特点.

证法2记si=a1+a2+…+ai(i=1,2,…,n),约定s0=0,则2si=(a1+ai)+…+(ai+a1)≥iai+1.

n=1时，命题显然成立.故原不等式成立.

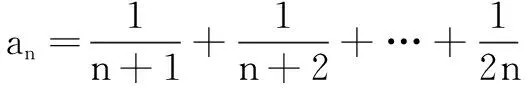
当n=3时，易知加强命题成立.

综上，猜想的结论成立.

评注此题还有以下几种求解方法，供读者参考.

解法2(运用积分，通过面积比较)

解法3(构造函数法)

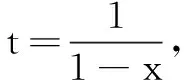
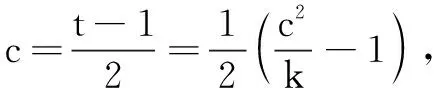
评注此题虽然不是直接按照数学归纳法的步骤去证明，但其中蕴含的思想依然是数学归纳法(翘翘板归纳法).

总之，数学归纳法作为解决有关正整数命题的常用方法,在解题过程中起着十分重要的作用．数学归纳法有方便着手、思路清晰等显而易见的优势；同时数学归纳法形式众多,有第一数学归纳法、第二数学归纳法、跳跃归纳法、反向归纳法等等形式.读者可以继续深入研究数学归纳法在有关正整数命题中的妙用．