一类条件最值问题的多角度探究——以一道联考试题为例

张剑平

(浙江省金华市第六中学，321000)

条件最值问题是每年高考、联考常考的内容之一,其解题方法灵活多样,难度较大,备受命题者青睐.笔者以一道联考试题为例,从基本不等式、权方和不等式、换元法、三角代换等多角度探究一类条件最值问题的解法,并举例说明权方和不等式在解决一类条件最值问题的应用,以期抛砖引玉.

一、柯西不等式、权方和不等式简介

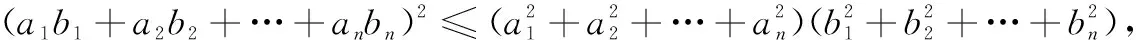
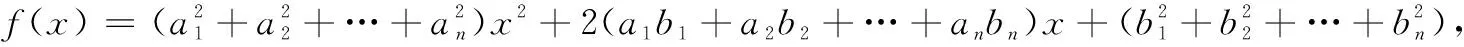
由柯西不等式，很容易得到权方和不等式的二维形式.

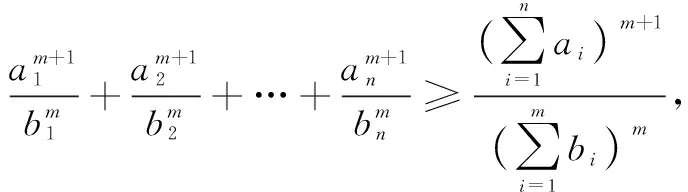
二、联考题解法探究

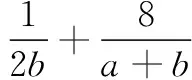
本题为浙江省2020学年第一学期“山水联盟”开学考试的第15题.学生解答此题时，有的因找不着条件最值求解思路而放弃，有的因等价变形时目标不明导致半途而废.现将其解答整理如下.

解法1换元法+基本不等式

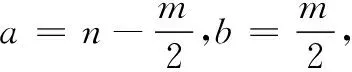
评注这类条件最值问题直接用基本不等式无法求解.通过换元后代换“1”,再使用基本不等式,水到渠成、解法自然．

解法2整体思想+基本不等式

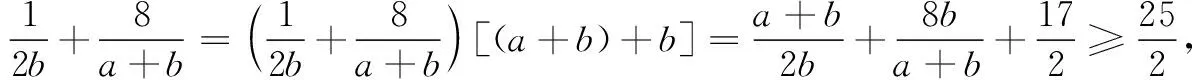
评注此解法简洁明了,但将a+2b=1转化为(a+b)+b=1,进而使用代换“1”是个难点,要求学生具备整体思想.

解法3消元法+权方和不等式

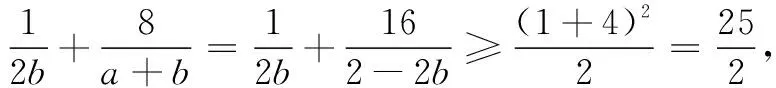
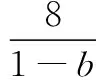
解法4三角换元+权方和不等式

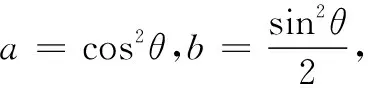
评注由条件a+2b=1很容易想到三角换元法,进而使用权方和不等式可使问题获解．

三、拓展应用举例

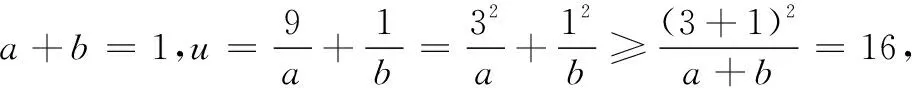
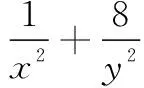
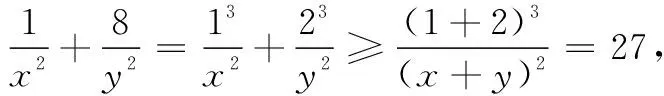
人教版教材中只介绍了基本不等式,在我们的常规教学中,往往非常注重解题的常规思路,解题方法循规蹈矩,让学生不敢有奇思妙想．如果教师能在教学过程中适当地补充一些课本之外的知识,引导学生一题多解,从不同角度思考问题,可以使学生的解题思路开阔,妙法顿生,解题速度提高．利用权方和不等式解决这类条件最值问题,其思想方法新颖别致、独树一帜,有利于提高学生的思维品质．