探究疑点 提升能力——一道解三角形题的教学思考

陈凌燕

(福建省仙游金石中学，351200)

三角函数是高中数学中一类重要的基本初等函数,它关联数学多个知识模块,既包含了三角恒等变换及不等式等“数”的知识,还兼具解三角形等“形”的内涵,是增进学生数学理解能力的重要载体.本文通过一道三角问题求解的疑点探究,探索教学过程中如何适时提高学生综合分析处理问题的能力.

一、问题呈现

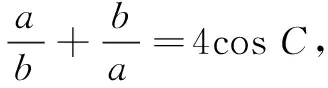
学生测试的结果不出所料:几乎全军覆没!考后了解学生,发现其思维过程几乎相同,得到的解法如下.

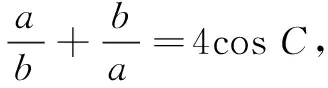
又由a+b>c=2,得a+b+c>4,故∆ABC周长的取值范围为(4,6].

二、源头探索

三、多解生成

视角1由不等式入手,直接求a+b的取值范围

视角2运用消元法,化归为单变量函数求值域

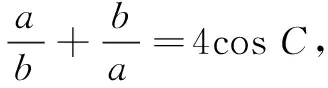
评注本解法通过消元,将要求的两变量表达式a+b转化成单变量k的函数,求其值域.

视角3采用三角换元,化归为三角函数求值域

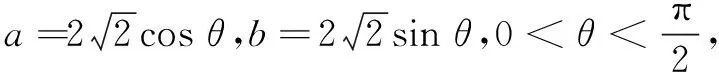
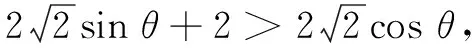
评注a2+b2=8具有熟悉的圆的方程特征形式,三角换元是解决“已知x2+y2=r2,求ax+by(a,b∈R)的取值范围”这类问题的典型方法.

视角4从解析法入手,探究轨迹求取值范围

正解4同上得a2+b2=8.设A(-1,0),B(1,0),C(x,y)(y≠0),则有(x+1)2+y2+(x-1)2+y2=8,整理得x2+y2=3,即动点C在圆x2+y2=3上,由此再求|BC|+|AC|的范围.

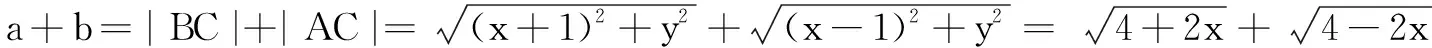
评注通过解析法得出动点C的轨迹,活化了对a+b取值范围探索的途径,降低了问题求解的难度,彰显了解析法以数助形的强大威力.

四、教学思考

1、注重问题“源头”探究,实现思维“活水”长流

任何事物都有矛盾,要抓住其主要矛盾,集中力量解决.教师在教学中要善于发现激发学生思维的关键问题,抓住这个“源头”,引导学生从自身的认知角度与学习经验出发,通过思考、分析和解决问题,使学生有思有得,同时享受其中的乐趣,做到乐学数学.

2、在多解中求同,认识本质,提升能力

学生不同的思维给出不同的解法,要从各种不同的解法中认识问题的本质,提升学生的综合能力.如本题中动三角形的本质是顶点C可变动,如何从不同的角度对其进行描述,就可产生各种不同的求解过程, 体现了数学不同知识模块的相互渗透性. 对问题本质的认识越透彻,就越能直指问题核心,简化问题处理过程.

3、总结活动经验,强化知识体系建构

学生给出问题的解法之后,教师要引导学生及时总结活动经验,根据其所采用的知识方法实现数学概念与知识网络的整体构建,让学生对知识有更深一层的理解.要帮助学生理清问题求解的层次和步骤,让学生感悟其中蕴含的数学思想,逐步建构自己的系统解题方法.