巧用主元思想 破解多元问题——以2020年高考数学试题为例

黄昌毅

(福建省厦门第一中学, 361003)

在多变元的数学问题中,常常有一些变元处于主导地位,我们称之为主元.按照主元的某种形式对问题进行整理,借以发现问题所隐含的特殊结构,以便找到相应的策略,使问题获解.像这样一种通过确定主元来探索解题途径的方法,称之为主元法[1].

多元问题是高考考查的热点、难点,在不等式、解析几何、函数导数问题中频繁出现,笔者以2020年高考题为例,列举主元思想在高考试题中的精彩应用.

例1(2020年全国高考题)设a,b,c∈R,a+b+c=0,abc=1.

(1)证明:ab+bc+ca<0;

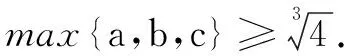
解(1)略.

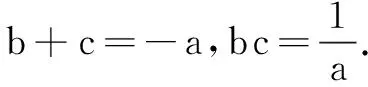
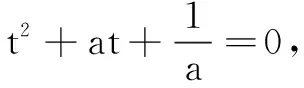
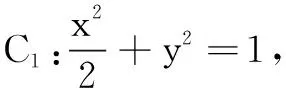
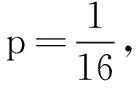
(2)若存在不过原点的直线l使M为线段AB的中点,求p的最大值.

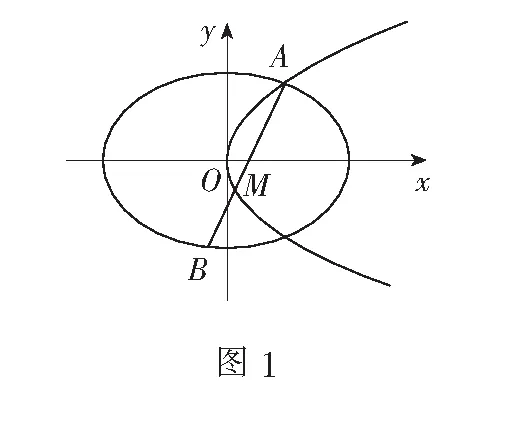
解(1)略.

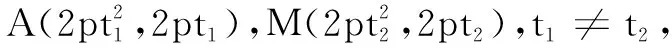
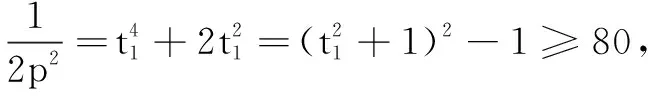
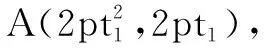
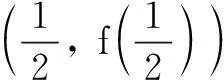
(1)求b的值;

(2)若f(x)有一个绝对值不大于1的零点,证明:f(x)所有零点的绝对值都不大于1.

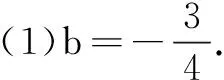
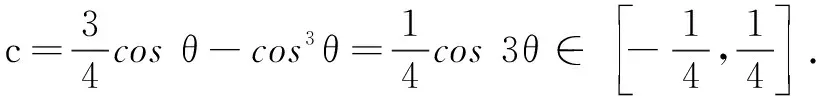
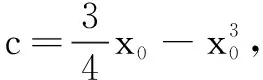
例4(2020年山东高考题)已知函数f(x)=aex-1-lnx+lna.

(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;

(2)若f(x)≥1,求a的取值范围.

解(1)略.

(2)依题意,有f(1)≥1,得a+lna≥1.设φ(a)=a+lna,易知φ(a)单调增,结合φ(a)=a+lna≥1=φ(1),可得a≥1.下面证明a≥1满足题意.

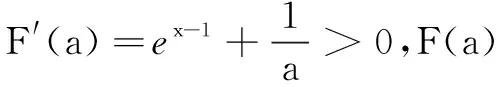
易证明lnx≤x-1,x≤ex-1,当且仅当x=1时取等号.因此有ex-1-lnx≥x-(x-1)=1,当且仅当x=1时取等号.

综上,a的取值范围是[1,+∞).

评注本题若以x为主元求f(x)的最小值,则计算过程繁杂;而以a为主元,则由单调性得F(a)≥F(1),可快速消元,化多元问题为单元问题,简化了计算,降低了求解难度.

例5(2020年全国高考题)已知函数f(x)=ex+ax2-x.

(1)当a=1时,讨论f(x)的单调性;

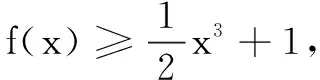
解(1)略.

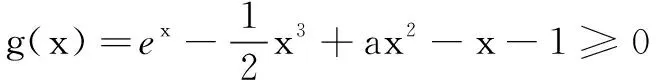
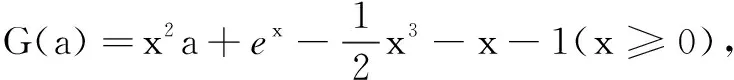
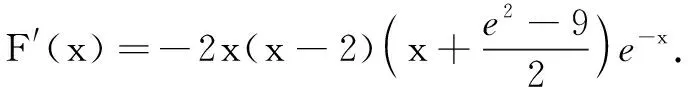
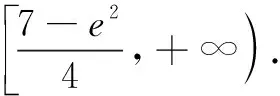
例6(2020年天津高考题)已知函数f(x)=x3+klnx(k∈R),f′(x)为f(x)的导函数.

(1)略;

(2)当k≥-3时,求证:对任意x1,x2∈[1,+∞),且x1>x2,有

解(1)略.

(2)题设不等式等价于(x1-x2)[f′(x1)+f′(x2)]-2[f(x1)-f(x2)]≥0.

以x1为主元,构造函数h(x)=(x-x2)[f′(x)+f′(x2)]-2[f(x)-f(x2)],x>x2≥1,则

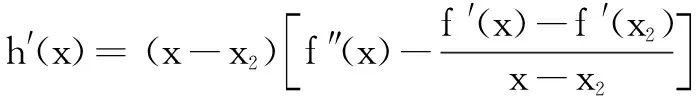
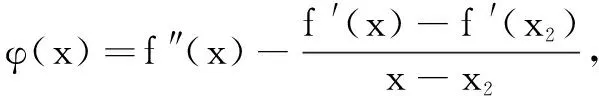
所以h′(x)≥0恒成立,即h(x)在(x2,+∞)单调增,可得h(x)≥h(x2)=0,即题设不等式成立.

评注本小题观察出x1,x2存在不等关系,故选择x1(也可选择x2)为主元构造函数并证明h(x)≥0;特别发现h(x2)=0,则需证明h(x)在(x2,+∞)单调递增即可.这样将多元问题转化为一元函数单调性证明,大大简化了运算.

主元思想是解决多元问题的有效方法,确定主元是解决这类问题的关键.确定主元,可将多元问题转化为单元问题,将复杂问题转化为简单问题,大大简化运算.