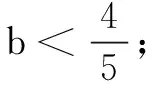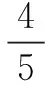例说实数大小比较的常用方法
王忠诚
(湖南省炎陵县第一中学,412500)
比较大小是高中数学中常见的题型,也是高考中常考常新的一类问题.这类问题通常以不等式的基本性质为主要依据,涉及不等式、函数等多方面的数学知识及数学思想方法,具有涉及面广、立意新、角度新、解法灵活多样等特点,能多方面考查同学们分析问题、解决问题的能力.本文以2020年高考真题为例,谈两个实数大小比较的常用方法.
一、作差(商)比较法
例1(2020年全国高考题)已知2a+log2a=4b+2log4b,则( )
(A)a>2b(B)a<2b
(C)a>b2(D)a 分析设f(x)=2x+log2x,利用作差法结合f(x)的单调性即可得到答案.也可以用取特殊值利用函数的单调性用排除法. 解法2由2a+log2a=4b+2log4b=22b+log2b,取b=1,得2a+log2a=4. 令g(x)=2x+log2x-4,则g(a)=0,且易知g(x)在(0,+∞)单调增,g(1)<0,g(2)>0,所以g(x)在(1,2)内有唯一的零点a,即此时a<2b=2,且a>b2=1,可排除A,D. 同理,取b=2,得2a+log2a=17.令函数h(x)=2x+log2x-17,则h(a)=0,且易知h(x)在(0,+∞)单调增,h(3)<0,h(4)>0,从而h(x)在(3,4)内有唯一的零点a,故此时a 综上,选B. 评注本题主要考查函数与方程的综合应用,涉及到构造函数,作差并利用函数的单调性比较大小,考查学生观察能力、运算能力、推理判断能力与灵活运用知识的综合能力. 例2(2020年山东高考题)已知a>0,b>0,且a+b=1,则( ) (C) log2a+log2b≥-2 分析根据a+b=1,结合基本不等式及二次函数知识求解. 由a-b=2a-1>-1,得2a-b>2-1,故B正确. 综上,选ABD. 评注本题主要考查不等式的性质,综合了基本不等式、指数函数及对数函数的单调性,侧重考查逻辑推理与数学运算的核心素养.作为新高考中的多项选择题,不等式的有关判断是很好的载体. 例3(2020年全国高考题)若2x-2y<3-x-3-y,则( ) (A)ln(y-x+1)>0 (B)ln(y-x+1)<0 (C)ln|x-y|>0 (D)ln|x-y|<0 解由条件可得2x-3-x<2y-3-y.令f(t)=2t-3-t,则f(x) 又由y=2x在R上单调增,y=3-x在R上单调减,易知f(t)在R上单调增, 因此x 评注本题考查指数式的大小判断问题,解题关键是能够通过构造函数的方式,利用函数的单调性得到x,y的大小关系;同时,考查了转化与化归的数学思想及逻辑推理、数学建模与数学运算等核心素养. (A)a (C)b 分析利用指数函数与对数函数的性质,即可得出a,b,c的大小关系. (A)a (C)b 例6(2020年全国高考题)已知55<84,134<85.设a=log53,b=log85,c=log138,则( ) (A)a (C)b 解由题意,可知a,b,c∈(0,1). 所以a 综上,a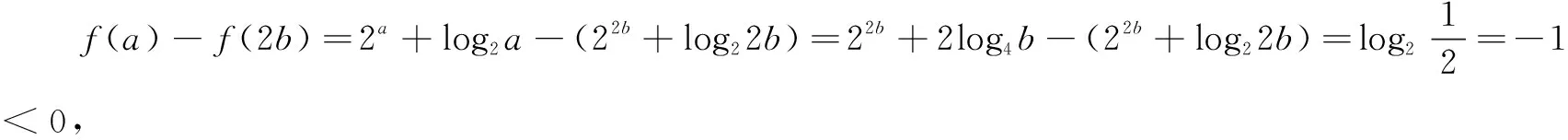
二、不等式法
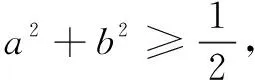

三、利用函数的单调性等性质

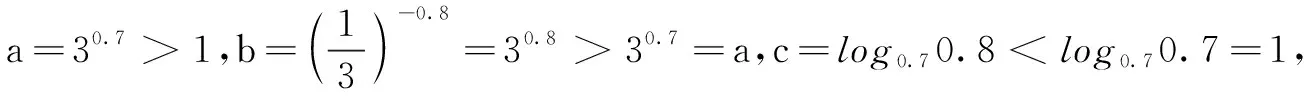


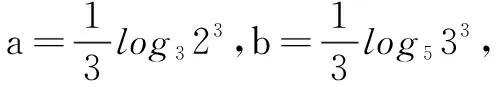
四、综合应用