多元并行 谁主沉浮
宋 磊
(上海市南汇中学,201399)
求解多元变量综合问题是高中数学一大难点,主元思想是解决此类问题的一大利器.本文拟通过典型例题剖析主元思想的运用.
一、甄选主元,峰回路转
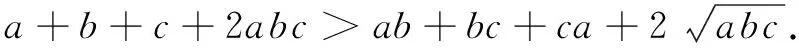
分析不等式中a,b,c地位相等且取值范围已知,不妨视a为主元,b,c为参数,则此式简化为一元不等式,问题更容易入手.

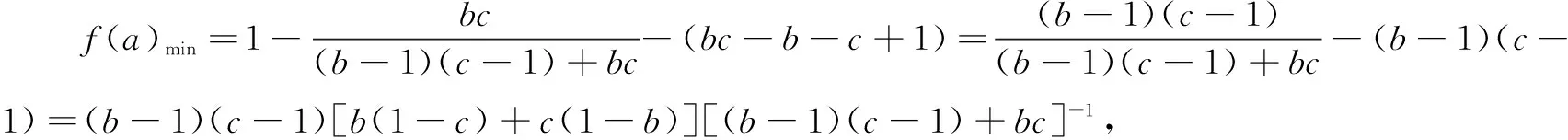
评注此类题目的共同特点是变量太多,让人眼花缭乱.甄选主元可以达到减元的目的,运用函数思想方法求解,使问题求解取得“峰回路转”的效果.
二、反道而行,柳暗花明

分析本题按常规思路是利用根的分布来解决,其中过多的分类讨论和繁琐的运算让学生望而生畏、步履维艰.不妨解放思想,更换主元,反道而行,使问题变得简洁明了.
视角1变更主元,将m,n当作主元,x当作参数.

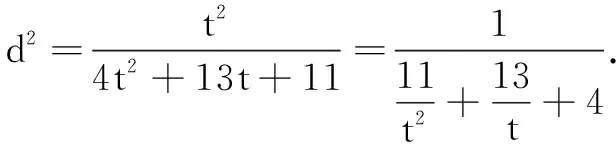

视角2变更主元,以m为主元.
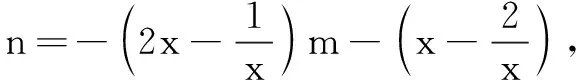
评注“横看成岭侧成峰,远近高低各不同”,同一事物从不同角度看,我们会有不同的认识.有些题目按照常规思路行不通,若能摆脱思维定势的束缚,及时更换观察问题的角度,灵活、机敏地挖掘问题中的特征与本质,追本溯源,主客换位思考,往往会有“山穷水尽疑无路,柳暗花明又一村”的豁然开朗之感.
三、交替轮换,别有洞天

分析本题难度在于题目条件与题目要求都是三元变量,学生易被搞得晕头转向.尝试甄选主元,甚至可以考虑多次甄选,轮流做主的做法,或许别有洞天,另有一番景象.
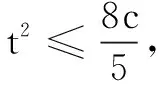
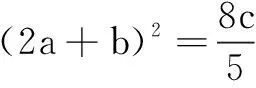
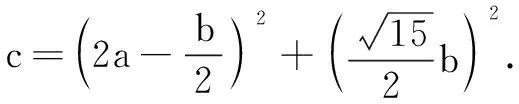
评注本题是多元变量最值问题,以上两种解题方法均从题目条件中选取主元,并且通过换元加以解决,将问题转化为新元的知识背景下去研究,从而可以把分散的条件联系起来,把复杂问题简单化,陌生问题熟悉化.其中解法1选了两次主元,轮流做主,问题迎刃而解.
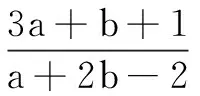
分析将所求代数式整体作为主元考虑.


(*)
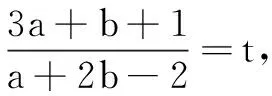

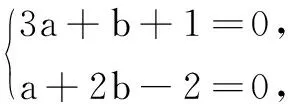

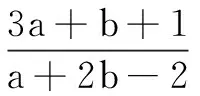
主元思想在中学数学中有着广泛的应用,若主元甄选得当,不但解题思路清晰,而且解法简洁明快.主元思想也是解题的一种重要思想方法,蕴含了转化与化归的数学思想,体现了辩证思维以及和谐统一、普遍联系的哲学观点,若能灵活运用,必将事半功倍.
——一道试题的解法剖析

