反思促成长

周东

摘要：问题是数学的心脏，是教学的核心。初中数学教师在解题教学中，如果没有题后反思，数学思维就会停滞不前，要培养学生的解题能力，就要和学生一起反思，养成题后反思的习惯。笔者认为，一要反思学生思维的受挫点，弥补知识的漏洞；二要反思解题路径，寻求一题多解；三要反思题目的不变性，研究解题规律；四要反思一题多变，提高思维的变通性。

关键词：解题规律；解题能力；教学反思

中图分类号：G633.6文献标识码：A文章编号：1992-7711（2020）06-0069

案例：某数学课分析试题，如图直角三角形ABC，∠ABC=90°，AB=6，BC=3，将△ABC沿着斜边AC对折，点B落在点B′处，过B′作BD垂直于直线AB，D为垂足，求CD的长。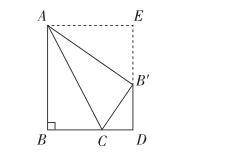

分析：本題利用对折即轴对称的性质，可以得出∠AB′C等于90°，可以利用直角三角形B′CD勾股定理来列方程求解。但是CD、B′D的长度是未知的，如何找到这两条边的关系成了解决这个问题的关键。根据∠AB′C=90度，可以联想到K型图，向外补形就可以得到△CDB′和△BEA相似。相似比为1∶2，可以设CD=X，则B′E=2X，B′D=6-2X，由勾股定理就可以列方程x2+（6-2x）2=32求解即可。

此时下课铃响起，为了不拖堂，笔者就说这个图还有什么规律，请大家课后再去研究。课后一个姓吴的学生找到笔者说：“老师我发现△CDB′的三边之比为3∶4∶5。”笔者当时一愣，这个可是笔者本人都没发现的规律。“真的吗？”笔者说，结果一算真的是这样，就是这样一个三边关系，然后我们就一起把这规律写成“如图，当BC∶AB=1∶2时，沿着AC折叠得到直角三角形B′CD的三边之比为3∶4∶5”，而笔者就把这个定理命名为“吴氏定理”，这时这位吴同学甭提有多高兴了。

又过了一天，吴同学又把他的定理扩充了“如图，当BC∶AB=1∶3时，沿着AC折叠得到直角三角形B′CD的三边之比也是3∶4∶5，”“相同吗？”笔者问，“一个是横∶竖∶斜=3∶4∶5，另一个是竖∶横∶斜= 3∶4∶5”。

“厉害，不愧为我们班的数学天才！”笔者及时给予肯定，激发了他更多的数学热情。此后，在平时的教学中我们又多了一个“吴氏定理”的应用。从此以后这位吴同学学习数学的积极性空前高涨，最后以优异的成绩提前被重点中学录取。

初中数学教师很多时间都花在解题上。但是题目千变万化，即使做得再多也不可能做完。数学家曾说过，数学问题的解决仅仅只是一半，更重要的是解题之后的回顾。一道数学题经过一番冥思苦想解出答案后，如果不进行反思，那么只会做这一题，跟学生讲，学生最多也是明白这个题目。进行认真反思梳理，研究规律，发现不变性，可以点拨解题思想方法，大大提高学生的解题能力，达到做一题会一类的效果。那么，教师如何反思？反思什么呢？

一、反思学生思维的受挫点，弥补知识的漏洞

在问题解决之后，反思解题过程是否遗漏已知条件或隐含的条件？解题过程多走了哪些思维回路？是否拘泥于思维定式，照搬了熟悉的解法？通过这样不断地质疑、不断改进，让解题过程更具有合理性、科学性、简捷性。

1.学生对K型图的理解不深刻，认为△ABC和△CDB′是一个K型图相似，求出了错误的答案。这里∠ACB′和∠ABC、∠CDB是不相等的，因此这两个三角形是不能证明相似的，我们应该加强一线三等角本质特征的认识，加深对相似判定的理解。

2.用勾股定理列方程出错，不能找出CD和DB′的关系。

3.数学思想方法的欠缺，找不到问题的出发点。这就要加强学生分析问题能力的培养。

二、反思解题路径，寻求一题多解

在问题解决之后，反思能否开辟新的解题通道？解题过程思维、运算能否变得简捷？通过这样不断质疑、不断改进，寻找一题多解的方法，从而提高思维的广度。

通过反思，此题建立了“对折——全等——勾股定理列方程求解，补形——一线三等角——相似表示未知的两边”这样一个解题思路，形成一定的解题方法。

2.把直角对折，若求边长，常设未知数，找到直角三角形利用勾股定理、方程思想可以解决。

3.角平分线+平行必有等腰三角形、K型图相似、勾股定理列方程等思想方法，向外补形和向内分割的添加辅助线的方法。

四、反思一题多变，提高思维的变通性

解题之后反思把这个题目放在矩形中就可以变式出很多的题目，通过变式的练习，不断地探究问题的知识结构和系统性。能否对问题蕴含的知识进行纵向深入地探究？能否加强知识的横向联系？把问题所蕴含孤立的知识“点”，扩展到系统的知识“面”，通过不断地拓展、联系、加强对知识结构的理解，进而形成认知结构中知识的系统性，提高学生思维的变通性，提高解题的能力。

例如：在矩形ABCD中，AB=6，BC=8，点E是BC上的一动点，把△ABE沿AE折叠。

1.若B点对应点B′恰好落在∠BCD的平分线上，求B′C。

2.若B点对应点B′恰好落在矩形的对称轴上，求BE。

3.若点E落在点C处，B′E和AD相交于点F，求△AFE的面积。

……

总之，问题与问题之间不是孤立的，许多表面上看似无关的问题却有着内在的联系、共性的知识、不变的规律、相同的思想方法，解题不能就题论题，要题后反思，构建知识网络，提炼数学思想、数学方从而提升解题能力，让学生脱离题海。

（作者单位：浙江省金华市武义县实验中学321200）