基于PSO-GA-BP神经网络的视觉伺服控制系统

赵 航, 岳晓峰, 方 博, 袁晓磊, 马国元, 郭宋吾铭

(长春工业大学 机电学院, 长春 130012)

0 引 言

1979年Hill等[1]提出视觉伺服技术, 目的是利用机器视觉进行图像获取、 处理和反馈以实现对机器人的控制。近年来, 由于计算机性能和图像处理技术的大幅度提高, 机器视觉伺服技术虽然获得了很大进步[2], 但同时也存在很多问题, 图像采集和处理精度、 速度都偏低, 伺服系统结构复杂、 计算量大, 严重影响了视觉伺服系统的广泛应用[3]。

传统的基于图像视觉伺服系统是用雅克比矩阵计算估计图像特征和机器人位姿变化的关系, 系统结构复杂且计算量大[4], 目前, 在多种图像雅可比伺服控制方法中[5-8], 基于神经网络的视觉伺服控制系统的研究比较多[9-12]。Zhong等[13]提出一种基于卡尔曼-神经网络滤波的图像伺服控制方法, 利用神经网络作为误差估计器, 对机器人系统建模误差以及动态噪声误差进行在线估计与补偿, 提高了卡尔曼滤波的稳定性； Gao等[14]设计了自适应神经网络控制器, 利用估计的全局位姿信息对水下机器人进行跟踪。利用单隐层神经网络和滑模控制器对动态不确定性和外部干扰进行补偿, 保证了跟踪误差的收敛性； 房德君[15]提出了一种基于熵聚类神经网络算法的机械手运动控制器, 使用熵聚类算法获取原始数据的聚类中心数和值, 以确定神经网络结构和基函数中心值； Gu等[16]利用模糊神经网络估计图像特征变化率与机器人关节角之间的映射关系, 设计了一种新型机械手控制器； Xu等[17]利用双目视觉相机获取三维空间信息, 然后使用神经网络控制神经元的非线性变换能力； 杨马英等[18]利用BP神经网络建立控制器模型, 并将神经网络控制器分为全局与局部两部分, 通过切换控制器提高伺服控制精度。通过研究国内外学者提出的方法, 发现许多使用神经网络解决视觉伺服控制问题的方式存在训练时间长, 收敛速度慢等弊端, 将粒子群算法和遗传算法结合, 收敛速度将更快, 改善全局收敛性能, 计算量少且鲁棒性更高。

笔者结合粒子群算法和遗传算法优化BP(Back Propagation)神经网络的权值和阈值, 设计神经网络学习图像特征空间到机器人运动空间的映射关系, 并将基于粒子群遗传算法优化的BP神经网络控制器应用于IRB1200机器人的视觉伺服控制系统中。

1 基于图像的视觉伺服系统

基于图像的视觉伺服控制系统结构如图1所示。摄像机系统用于收集图像特征信息, 经过图像处理后, 将目标图像特征与期望图像特征进行比较, 如果两者之间存在误差值, 则视觉控制器就会将误差值转换成机器人关节角度值, 这时机器人控制器就会发出指令控制机器人末端执行器向目标运动, 直到图像平面中图像特征误差为零, 视觉伺服任务结束。

图1 基于图像的机器人视觉伺服控制系统结构Fig.1 The block diagram of image-based robot visual servo control system

2 粒子群遗传算法优化BP神经网络

粒子群优化算法(PSO: Partical Swarm Optimization)是通过模拟鸟群捕食行为设计的一种群智能算法, 但其存在一些不足, 例如过早收敛和容易陷入局部极值, 这主要归因于搜索空间中种群多样性的损失, 而遗传算法的交叉变异操作可以更好地保证种群多样性。PSO-GA-BP(Particle Swarm Optimization-Genetic Algorithm-BP)算法是通过粒子群和遗传融合算法优化BP神经网络的权值和阈值, 该算法以粒子群算法为主体, 并在其中融入遗传算法, 结合两种算法的优势, 融合后的算法收敛速度更快, 全局收敛性能更好, 计算量少且鲁棒性高。PSO-GA-BP算法实现步骤如图2所示。

1) 初始化粒子种群、 粒子群算法和遗传算法所需参数。

2) 计算粒子的适应度值并寻找Pbest和gbest。利用适应度函数式计算粒子适应度值f(t), 将误差平方和E(t)的倒数定义为粒子适应度函数, 如下所示

(1)

(2)

其中U为种群规模,yi为预测输出,di为期望输出。由此可见, 适应度值越小则误差越大, BP神经网络的预测精度就越高。

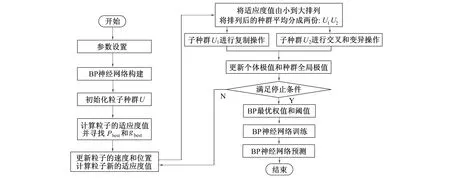
图2 PSO-GA-BP算法流程图Fig.2 The flow chart of PSO-GA-BP algorithm

3) 使用粒子群优化算法对种群U进行寻优。利用

vil(t+1)=ωvil(t)+c1R1(pil(t)-xil(t))+c2R2(pgl(t)-xil(t))

(3)

对粒子的速度进行更新, 采用

xil(t+1)=xil(t)+vil(t+1)

(4)

对粒子的位置信息进行更新； 其中i=1,2,…,n,l=1,2,…,m,vil为粒子速度,xil为粒子位置,pi为粒子i的最佳位置,pg为粒子群中所有粒子i的最佳位置,t为进化代数；ω为惯性权重,c1、c2为学习因子,R1、R2为[0,1]范围内的随机数。将适应度值由小到大排列后的种群分为U1、U2, 其中适应度较好的为U1、 适应度较差的为U2。

4) 引入遗传算法, 适应度较好的子种群U1直接复制到下一代中, 对适应度较差的子种群U2进行随机交叉和变异操作。

对粒子i和粒子j的速度进行交叉运算, 则有

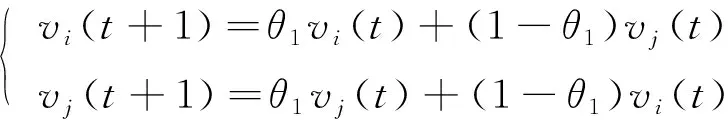
(5)

对粒子i和粒子j的位置进行交叉运算, 则有

(6)

其中θ1和θ2为[0,1]范围内的随机数。

5) 更新个体极值Pbest和种群全局极值gbest。比较计算得到的新适应度值和个体极值Pbest的适应度值, 更新每个粒子最好的适应度值和最好的位置Pibest值, 然后比较计算得到的新适应度值和群体极值gbest的适应度值, 更新粒子群的最好位置gbest值。

6) 重复步骤2)～步骤5), 如果最好适应度值达到收敛精度或迭代次数达到设定的最大次数, 则迭代终止, 将粒子群的最好位置作为BP神经网络的参数。否则继续进行重复迭代操作。

粒子群遗传优化算法结束时, 将得到的最优解输出为BP神经网络的权值和阈值, 重新训练神经网络, 然后进行仿真实验, 获得BP神经网络的预测函数输出。

3 BP神经网络结构设计

图3 BP神经网络结构图Fig.3 The structure of BP neural network

BP神经网络学习算法是目前最成功的神经网络学习算法之一, 是一种多层的前馈神经网络, 其主要特点为信号是前向传播的, 而误差是反向传播的。BP神经网络由输入层、 隐藏层和输出层组成。假设工作空间中的目标工件是正方形, 选取目标的4个顶点A,B,C,D作为特征点, 则在图像空间中特征点对应为A′,B′,C′,D′。目标是控制机器人运动直到工件4个特征点的图像特征和期望图像特征点坐标重合。当前图像特征点位置坐标和期望图像特征点位置坐标之间的差值构成一个8维图像特征向量, 选取神经网络的输入为图像特征向量： Δx1, Δy1,Δx2,Δy2,Δx3,Δy3,Δx4,Δy4。输出是6个当前关节角与期望关节角的差值： Δq1,Δq2,Δq3,Δq4,Δq5,Δq6。BP神经网络的学习阶段是通过移动机器人末端执行器记录相应关节角的变化获取训练样本, 同时记录相应的图像特征变化, 离线对BP神经网络进行训练； 网络的执行阶段是根据神经网络的输入计算期望的关节角变化。

BP神经网络结构如图3所示。由于图像特征向量是8维, 选取 BP网络的输入节点数为8； 由于机器人具有6个关节角差值, 选取BP网络的输出层节点数为6。BP神经网络隐含层一般可以用试凑法确定, 常用经验公式为[19]

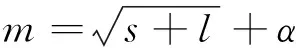
(7)

其中m为隐含层节点数,s为输入层节点数,l为输出层节点数,α为1～10之间的整数。笔者输入和输出节点数分别为8和6, 根据经验公式求得隐含层节点数为5～14。如果隐层节点数太少, 则网络可能性能不佳； 如果隐层节点数太多, 虽然可以减小网络的系统误差, 但会使网络训练时间延长, 且训练容易陷入局部极小值。通过多次实验选取隐含层节点数为10。

4 视觉伺服控制器设计及仿真

4.1 数据采集

为了获得粒子群遗传优化BP神经网络的训练样本, 根据图1的控制系统结构, 利用Matlab软件中的机器人工具箱(Robotics Toolbox)搭建了一个六关节IRB1200机器人模型, 并构建IBVS仿真系统。随意移动机械手末端执行器的位置, 记录图像特征变化差值和对应的机械手关节角变化, 得到500组样本, 其中450组作为训练样本, 50组作为测试样本。

4.2 模型学习

根据图2和图3建立PSO-GA-BP神经网络模型, 在Matlab软件上编写程序实现所需功能。需要多次运行程序得到良好的函数逼近性能, 根据程序结果的收敛情况将所需的参数设置为： BP算法的学习率μ=0.4, 动量因子η=0.8, 期望误差e=10-6。粒子群算法中, 种群规模U=80, 迭代次数为100次, 惯性权重ω=0.7, 两个学习因子c1=c2=2。在遗传算法中, 种群规模也为80, 迭代次数为100次, 交叉概率Pcross=0.6, 变异概率Pmutation=0.1。

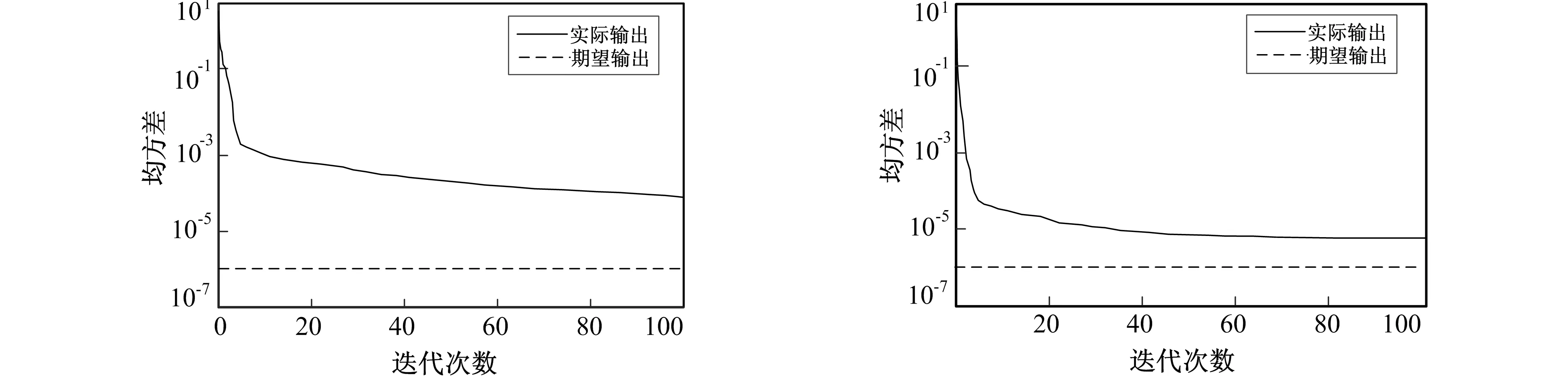
a BP神经网络曲线图 b PSO-GA-BP神经网络曲线图图4 训练曲线图Fig.4 The training curves

图4a和图4b分别反映了传统BP神经网络和粒子群遗传优化过的神经网络测试集的输出均方差。可以看出传统神经网络在迭代100次以内达不到期望输出精度, 而PSO-GA-BP神经网络收敛速度很快, 在不到第80步时就能收敛到8.176 3×10-6, 非常接近期望的输出精度值。实验结果表明PSO-GA-BP神经网络收敛速度明显高于传统的BP神经网络。

4.3 机器人视觉伺服

在视觉伺服控制系统中, 使用训练过的BP神经网络作为视觉控制器建立视觉伺服控制系统。在仿真实验中, 目标工件是一个正方形, 做以下假设：

1) 目标4个顶点在世界坐标系中的坐标为

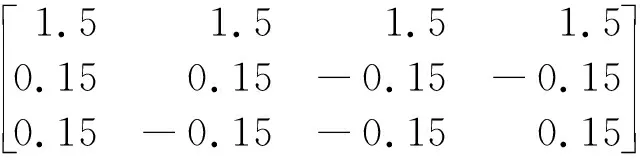
2) 期望的图像特征坐标为

3) 机器人的初始关节角为

q0=[1.519 4,1.116 5,0.681 9,-0.387 2,-1.033 8,-1.502 4]T

4) 摄像机的参数为： 焦距f=8 mm,α=β=800 00 pixels/m, 目标成像深度h=1.5 m, 图像中心点为(338,338), 控制器比例系数kp=1.5。采样时间为0.2 s。

笔者对基于PSO-GA-BP神经网络和复合雅可比矩阵J+伪逆的两种视觉伺服控制方法进行对比实验。结果如图5和图6所示, 由图5可以看出, PSO-GA-BP神经网络视觉伺服控制能更好地逼近图像特征误差值和关节角差值间的非线性关系, 由图6可以看出, 图像特征误差范数收敛速度很快, 在第20 s时就达到了4.762。

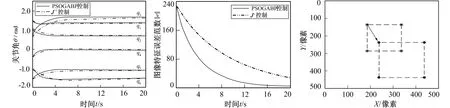
图5 机器人关节角轨迹 图6 图像特征误差范数曲线 图7 图像特征运动轨迹 Fig.5 The joint trajectory of robot Fig.6 The image feature error norm Fig.7 The motion track of image characteristic

5 结 语

相比于基于复合雅可比矩阵J+伪逆的视觉伺服控制系统, 笔者提出的基于PSO-GA-BP神经网络视觉伺服控制方法极大地简化了计算的复杂程度, 准确地建立了图像特征变化和关节角变化间的非线性关系。在Matlab环境下对IRB1200机器人组成的视觉伺服控制系统进行仿真实验, 实验结果表明, PSO-GA-BP神经网络视觉伺服控制器具有收敛速度快、 训练精度高的特点, 在笔者设定的实验条件下, 图像位置平均误差约为2个像素, 机械臂末端执行器能较好地达到预期位置, 且图像特征误差范数收敛速度快, 约20 s就达到4.762, 系统运行效率较高, 具有良好的实用性能。