基于偏移量周期填充的QC-LDPC码构造方法
赵 明, 刘志鹏, 赵 岭
(1. 中国电子科技集团公司 电子科学研究院, 北京 100041; 2. 北京航空航天大学 电子信息工程学院, 北京 100191)
0 引 言
低密度奇偶校验卷积(LDPC-C: Low Density Parity-Check Convolutional)码是定义在稀疏奇偶校验矩阵上的一类卷积码[1-2], 其可对任意长度的数据进行连续编码和译码, 因此可以很好地应用于可变帧长的通信(如无线局域网)或连续模式的通信(如视频通信、 中继卫星高速数传)系统中[3]。LDPC-C码具有接近香农(Shannon)极限的译码性能和较低的编码复杂度[1-2,4]。其中准循环低密度奇偶校验卷积(QC-LDPC-C: Quasi-Cyclic LDPC-C)码对应的半无穷校验矩阵由一组循环移位矩阵(CPMs: Circulant Permutation Matrices)构成, 从而易于高效编码和译码, 且便于硬件实现[5-6]。
目前, 构造LDPC-C码需通过对LDPC分组码进行校验矩阵拆解。文献[1]提出基于LDPC分组码的校验矩阵并利用剪切、交换和重复的方法构造LDPC-C码。利用QC-LDPC分组码的循环移位子矩阵构造LDPC-C码对应的校验矩阵[5], 可简化矩阵构造的复杂度。文献[7]提出在LDPC-C码的构造中, 采用LDPC分组码的渐进边增长(PEG: Progressive Edge-Growth)构造方法。文献[8]提出利用LDPC码, 并采用基于图覆盖的方法构造LDPC-C码, 所构造的LDPC-C码性能优于相应的LDPC分组码, 同时分析了其中的卷积增益。文献[9]提出利用有限域的乘群, 并采用相关的修正方法获得可实现快速编码的LDPC-C码。此外, 还有其他构造LDPC-C码对应校验矩阵的方法[10-12]。
LDPC-C译码算法利用基于校验矩阵行的置信度传播(BP: Belief Propagation)迭代计算完成, 因此LDPC-C码, 特别是QC-LDPC-C码对应校验矩阵需考虑短环问题[13-14]。虽然LDPC-C码可利用对应的LDPC分组码进行构造, 但需对LDPC分组码对应的校验矩阵进行剪切、 交换和复制等操作, 而此时会改变矩阵的结构, 特别当LDPC-C码的码长、 记忆长度和周期为随机的正整数时, 无法确保得到的LDPC-C码对应校验矩阵不存在4环。并且, 若不考虑LDPC-C码对应校验矩阵的结构特点, 直接构造校验矩阵, 将会使构造算法的计算复杂度呈指数增长[15-22]。
为获得较好的译码性能, 尽可能提高所构造码的围长(girth)并避免短环, 特别是4环的存在, 笔者提出基于子矩阵偏移量周期性填充的QC-LDPC-C码构造方法。同时, 考虑到可实现快速编码, 在QC-LDPC-C码对应校验矩阵的构造中, 令每个校验行块中最右端子矩阵的校验部分子矩阵满足行和列的非负值个数均为1。所提构造方法基于QC-LDPC-C码对应的基矩阵构造, 利用基矩阵的周期性, 首先填充确定的校验行块中校验部分子矩阵的位置;而后利用基于子矩阵偏移量周期性扩展填充的方法, 周期性扩展所填充的对应位置, 并在周期性扩展每个对应位置时, 使由周期性确定的位置与即将填充的位置构成的矩阵可满足无4环的扩展矩阵结构。因此, 所构造的由基矩阵扩展的校验矩阵不存在4环, 即校验矩阵的围长至少为6。利用所提方法构造的QC-LDPC-C码可实现快速编码, 降低编码复杂度, 同时可获得较好的译码性能。
1 QC-LDPC-C码的主要构造框架
为降低译码设计实现的复杂度, 所构造的QC-LDPC-C码对应的校验矩阵H由基矩阵Hb扩展得到, 其中子矩阵扩展因子为b。对于码率为R=k0/n0的(n0b0,k0b0,M)QC-LDPC-C码, 其基矩阵

(1)
其中Bi(t)(i=0,1,…,M,t∈)是mb×nb=(m0b0/b)×(n0b0/b)阶矩阵。Hb中元素的取值范围为{-1,0,1,…,b-1}, 若元素为-1, 则扩展得到的子矩阵即为全零矩阵; 若元素为其他值, 则扩展为循环移位单位矩阵(CPIM: Circulant Permutation Identity Matrix), 元素值即为子矩阵的循环移位偏移量。
k0,n0的最大公约数是1, 且任意Bi(t)(i=0,1,…,M,t∈)是m0b0×n0b0=(n0-k0)b0×n0b0阶二元矩阵。其中M为码组的记忆块长度, 而ns=(M+1)n0b0为码的约束长度。若式(1)满足Bi(t+T)=Bi(t)(i=0,1,…,M,t∈), 则该码为周期性时变QC-LDPC-C码; 当T=1时, 该码为时不变QC-LDPC-C码。
为简化校验矩阵设计的复杂度, 同时考虑到校验矩阵的行重和列重分布, 在校验矩阵的构造中不能直接利用b0进行矩阵框架的构造, 否则可能无法满足所设计的行重和列重。因此, 提出利用子矩阵扩展因子b构造校验矩阵, 其中b0是b的整数倍。
2 基于偏移量周期性填充高效构造QC-LDPC-C码
2.1 QC-LDPC-C码对应校验矩阵的可快速编码结构
为利用迭代计算的方式实现快速编码, 需对QC-LDPC-C码对应基矩阵Hb的每行进行设计。这里要求Hb中B0(t)(t∈)的校验部分子矩阵满足行和列的非负数个数均为1(见图1)。
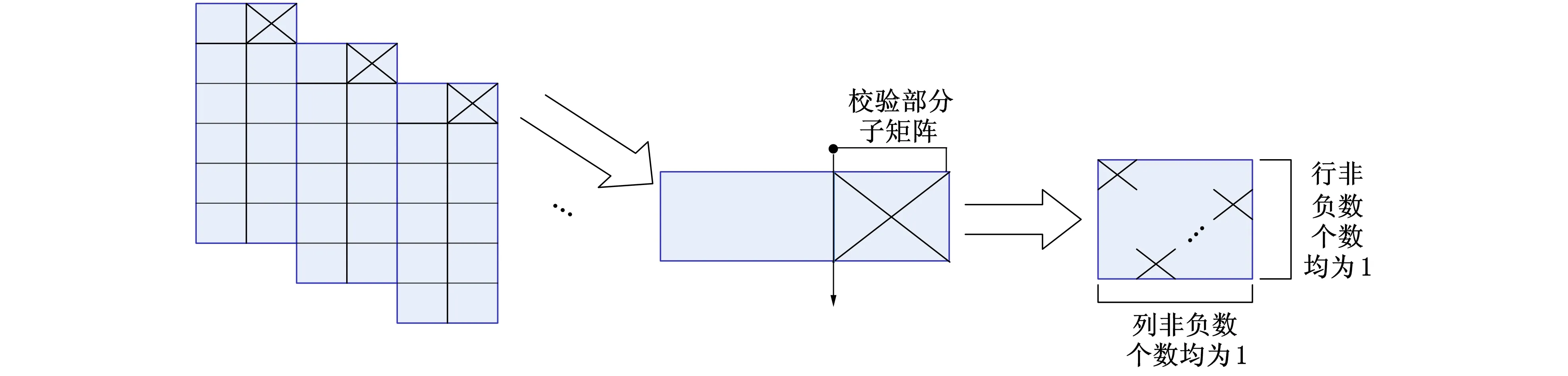
图1 B0(t)(t∈)的校验部分子矩阵的行和列非负数个数分布Fig.1 The numbers of non-negative values in each row and column of parity-check portion in B0(t)(t∈)
由图1可知,B0(t)(t∈)的校验部分子矩阵中各行非负值的位置集合是其所有可能行位置的排列组合, 即所有行不存在重复的非负值行位置。
同时, 为实现正确的基于迭代计算的快速编码, 需基矩阵Hb的每行中非负数的个数至少为2, 即要求每行除B0(t)(t∈)对应的校验部分外, 其余位置的非负数的个数至少为1。
2.2 基于偏移量周期性填充的QC-LDPC-C码构造
2.2.1 无4环的扩展矩阵结构
图2所示的基校验矩阵中存在4环, 其中Mi(1≤i≤4)为H中的非零子矩阵。此时若要求扩展后的矩阵不存在4环, 则
mod(q(M1)-q(M2),b)≠mod(q(M3)-q(M4),b)
(2)
其中q(Mi)表示非零子矩阵Mi的循环右移数值, mod(a,b)表示a对b整除后求余。

图2 非零子矩阵M1,M2,M3,M4在H中的位置处于4环结构中Fig.2 The positions of non-zero sub-matrices M1,M2,M3,M4 in H are in an length-4 cycle
2.2.2 基于偏移量周期性填充方法
在构造QC-LDPC-C码对应的基校验矩阵时, 可首先利用行位置的排列组合方法确定B0(t)中校验部分子矩阵非负数的位置。
将式(1)中QC-LDPC-C码对应基校验矩阵Hb的周期假定为T, 则在确定其余非负数的位置上, 比特填充的周期也为T, 同时在周期为T的对应位置上填充相同的值。因此, 只需完成周期T内的列构成的子矩阵的构造即可。同时为降低设计和计算的复杂度, 将校验矩阵H的围长设置为6, 即不存在4环。所以, 只需检验矩阵Hb中(T+2M)个包含完整约束长度的行构成的子矩阵的短环即可。于是, 笔者提出基于偏移量周期性填充的QC-LDPC-C码构造方法。
由于所考虑的基校验矩阵Hb的周期为T, 所以若Hb中存在4环, 则4环的一条竖边必在周期为T的校验列内, 因此4环的结构必在周期为T的校验列所包含的检验行中。同时, 所构造的部分基校验矩阵需使前Mmb行的行重至少为2, 因此所考虑的部分基校验矩阵为

(3)

假定已经构建了n(n≥0)列的校验矩阵HB满足所有的约束条件, 即对k=1,2,…,N, 第k列的列重正好为ak; 并且相应二分图的girth满足g≥6。现在考虑增加第(n+1)列到校验矩阵HB中, 新增的列用包含元素的个数至多为an+1的校验节点集合U1表示, 初始化为空。进一步假定, 已经在U1中加入了i(0≤i≤an+1)个校验节点。
对任一个校验节点1≤c≤M,Nc是指与c共享变量节点的所有校验节点的集合。对j≥2, 定义
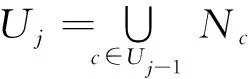
(4)
显然U2中每个校验节点肯定与U1中某个校验节点存在长度为2的路径。增加一个校验节点c′到U1中, 则c′和U1的每个校验节点间都存在一条长度为2的路径, 所以如果c′也出现在U2中, 就可确定长度为4的环的存在。因此为避免长度为4的环, 应该避免这个校验节点在U2中出现。因此, 为满足girth限制, 应尽量避免将集合U中的校验节点加到U1中。集合
U=U1∪U2
(5)
令D(c)为校验节点c的度数, 同时令
A= {c∈{1,2,…,M}|D(c) (6) 其中A是还没有达到最大重量的校验节点集, 则没有违反girth约束的可加到U1的校验节点集合即为A集合与U集合的差值, 可表示为 F0=AU (7) 如果F0为空, 当前girth将减少2; 如果g′降到小于4, 则算法停止。 于是, 提出的QC-LDPC-C码的构造方法如算法1所示。 算法1 输入参数:mb,nb,M,T,smax,{a1,a2,…,anbT}, {br1,br2,…,br(M+T)mb}, {P1,P2,…,PT} 填充确定的子矩阵部分: 1) Fori=0;i≤T-1;i=i+1 2) Forj=1;j≤mb;j=j+1 3) 确定B0(i)(Pi(j),nb-mb+1)的值 4) End For 5) End For 6) Fori=T;i≤T+2M-1;i=i+1 7) If mod(i,T)=0 8)B0(i)=B0(T) 9) Else 10)B0(i)=B0(mod(i,T)) 11) End If 12) End For 13) Forc=1;c≤mb(T+2M);c=c+1 14)D(c)=1;Nc={c} 15) End For 填充随机子矩阵部分: 17) Fort=0;t 18) Forn=0;n 19) Ifn≥nb-mb+1 20)A={mb(t+1)+1,mb(t+1)+2,…,mb(t+M+1)} 21)anT=anT-1 22) Else 23)A={mbt+1,mbt+2,…,mb(t+M+1)} 24) End If 26) Fors=0; (t+sT+i<=T+2M-1);s=s+1 27) 设置Bi(t+sT+i)(j,n)的数值 28) End For 30) Fori=0;i 31) sel_flag=0; 32) Forg′=g_max; (g′>=4sel_flag=0);g′=g′-2 33) 计算F0=AU0 34) If(g′≥6&&F0≠φ)‖g′=4 35) Ifg′=4 36) 依据算法2中的算法从F1中选择c* 37) Else 38) 依据文献[16]中的算法从F0中选择c* 39) End If 40) sel_flag=1,F1=F1c* 41)ii=⎣c*/mb」 42) Fors=0; (t+sT+ii<=T+2M-1);s=s+1 49)b=br-counter,A=A∩{∀d|D(d) 50) End If 51) End For 52) Else 54) End If 55) End For 56) End For 57) End For 58) End For 输出参数:HB,g′ 最后, 更新U=U∪V2(c)。只有当girth降低2时, 才需重新计算U。算法1的目的即加入第(i+1)个校验节点到U1中。如果失败, 整个算法将停止。 这里为降低计算复杂度, 对搜索的次数进行了简化。由于构造的基校验矩阵仅考虑不存在4环, 因此将循环搜索的次数设置为2, 由此可令构造矩阵的围长至少为6。 在算法1中, 从F1中选择c*的算法如下。 算法2 1) ∀c∈F1, 令U1(c)={c}; 2) ∀c∈F1, 计算U2(c), 并计算T0(c)=U2(c)∩U0; 3) ∀c∈F1, 计算S1(c)=|T0(c)|, 计算T1={c1∈F1: ∀c2∈F1,S1(c1)≤S1(c2)}; 4) ∀c∈T1, 计算S2(c)=D(c), 计算T2={c1∈T1: ∀c2∈T1,S2(c1)≤S2(c2)}; 5) 从T2中选择c*。 注意到算法1中, 如果已经添加了一个校验节点c到U1中, 然后设U1={c}, 并且计算 (8) V2(c)=U1(c)∪U2(c) (9) 算法1中的构造流程示意图如图3所示。假定构造的基矩阵Hb的列重均为3, 且Hb的周期为T。若矩阵Hb的参数设置为其他数值, 则可采用类似的方法进行构造。 图3 所提构造方法的流程示意图Fig.3 The flow diagram of proposed construction method 由于矩阵Hb的周期为T, 因此只要完成前Tnb列的构造, 即可依据矩阵的周期性得到Hb。在算法1中, 首先根据每个行块中B0(t),t∈[0,T-1]的校验部分子矩阵满足行和列的非负数个数均为1, 确定一个周期内B0(t)的校验部分子矩阵中非负值的位置, 而后进行周期性扩展, 即填充确定的子矩阵部分(图3中标记X的方格)。 在矩阵Hb的随机子矩阵部分的构造中, 只需得到前Tnb列的非负值位置即可, 而所要完成周期性填充的部分基校验矩阵HB的总列数为(T+2M)nb。因此, 在确定前Tnb列的每个非负值位置后, 需依据矩阵HB的周期, 填充以T为周期的对应位置(即完成第26~28行, 也即图3中周期T内未标记X的位置)。 由于需确定非负值位置的矩阵HB的总列数为(T+2M)nb, 因此在针对矩阵Hb的前Tnb列的构造中, 每个即将填充的非负值位置及其周期扩展后填充的位置都要与已填充的位置及其周期扩展后填充的位置构成联合矩阵, 并依据式(2)对此联合矩阵进行扩展矩阵结构4环检验。 于是, 利用所提的基于子矩阵偏移量周期性扩展填充的方法, 即可得到部分基校验矩阵HB的非负值位置, 而后依据矩阵的周期性, 得到基校验矩阵Hb的非负值位置。并且在构造过程中使Hb满足无4环的扩展矩阵结构的要求, 于是可确保由矩阵Hb扩展后得到的检验矩阵的围长至少为6, 即不存在4环。 2.2.3 计算复杂度分析 依据式(3)给出的部分基校验矩阵HB和算法1, 算法1中填充确定子矩阵部分可在O((T+M)mb)(即线性复杂度)内完成。 对算法1中的填充随机子矩阵部分, 假定构造的部分基校验矩阵HB的行、 列重平均值分别为a和b, 第33行计算A和U0的差集, 可在O((T+M)mb)内完成。针对联合矩阵中存在无4环结构的情形, 执行第36行从F1中选择c*(即算法2), 在最复杂的情形下需O(((T+M)mb)2)次运算。而针对联合矩阵中存在4环的情形, 执行第38行从F0中选择c*[16], 在最复杂的情形下也需要O(((T+M)mb)2)次运算。 于是, 每执行一次第30~56行的“For…End For”内循环, 复杂度为O(((T+M)mb)2)。这个循环最多执行a次, 复杂度为O(a((T+M)mb)2)。最后, 第 17~58行的两层外循环“For…End For”最多执行bT(T+M)mb/a次, 所以算法总体复杂度为 O(a((T+M)mb)2bT(T+M)mb/a)=O(bT((T+M)mb)3) 利用算法构造QC-LDPC-C码对应基校验矩阵时, 算法的总体计算复杂度如表1所示。 表1 构造算法总体的计算复杂度 为验证构造算法的译码性能, 使用具有不同码率和码长的LDPC-C码的校验矩阵进行仿真实验。实验是在二进制移相键控(BPSK: Binary Phase Shift Keying)调制和加性高斯白噪声(AWGN: Additive White Gaussian Noise)信道条件下, 使用不同的迭代次数及信噪比(SNRs: Signal to Noise Ratios)条件, 其中最大迭代次数为30次。针对IEEE 1901标准中LDPC-C码[3], 利用LBP译码算法所得的误码率(BER: Bit Error Rate,RBER)性能如图4所示。 在图4中, 码Ref-CC12-1901和Ref-CC23-1901分别是IEEE 1901标准中码率为1/2和2/3的LDPC-C码[3]。构造的QC-LDPC-C码CC-1和CC-2分别与码Ref-CC12-1901和Ref-CC23-1901具有相同的码率和行列重分布, 且两个码的周期均为3。其中码CC-1对应基矩阵的每个元素包含2列, 子矩阵扩展因子为2, 记忆块长度为108; 码CC-2对应基矩阵的每个元素包含3列, 子矩阵扩展因子为3, 记忆块长度为76。 图4表明, 构造码CC-1和CC-2的译码性能均优于标准中对应的码Ref-CC12-1901和Ref-CC23-1901。在图4中, CC-1和CC-2可利用构造的基校验矩阵实现基于迭代计算的快速编码, 即此时的编码复杂度只与基校验矩阵的行数和列重相关, 并且其译码过程可直接采用构造的基校验矩阵进行迭代计算。而Ref-CC12-1901和Ref-CC23-1901在编码过程中需要存储和利用完整的校验矩阵进行计算, 并且译码也需基于较为复杂的校验矩阵进行迭代计算。因此, CC-1和CC-2具有相对较低的编译码复杂度。 图4 码Ref-CC12-1901与CC-1, Ref-CC23-1901 图5 码Ref-CC2与CC-3在不同的 与CC-2在不同的SNR条件下的BER性能 SNR条件下的BER性能 Fig. 4 BER performance of the codes Ref-CC12-1901, Fig. 5 BER performance of the codes Ref-CC2 CC-1, Ref-CC23-1901 and CC-2 under different SNRs and CC-3 under different SNRs 图5所使用的码Ref-CC2为基于LDPC码构造的码率为2/3, 约束长度为2520的LDPC-C码[8]。构造的QC-LDPC-C码CC-3具有相同的码率和约束长度, 其对应基矩阵的每个元素包含4列, 子矩阵扩展因子为64, 码的周期为10。图5表明构造码CC-3比码Ref-CC2有更好的性能, 同时码CC-3具有较低的编译码复杂度。 由图4和图5可见, 采用笔者提出的方法构造的QC-LDPC-C码在相同或相近的条件下, 可获得更好的译码性能。同时, 由于构造码均为具有可实现快速编码的准循环码, 于是这些码相对具有较低的编译码复杂度, 更易于设计实现。 QC-LDPC-C码具有较低的编译码复杂度, 同时经过优化设计的码可获得逼近Shannon极限的译码性能, 并可对任意长度的数据进行连续编译码。但QC-LDPC-C码的构造需避免4环, 并且其校验矩阵的直接构造方法的计算复杂度较高。于是, 笔者提出基于偏移量周期性填充的QC-LDPC-C码构造方法。依据QC-LDPC-C码对应的基校验矩阵的周期性, 所提方法首先确定校验行块中最右端子矩阵的校验部分子矩阵的位置;而后在针对每个列中每个变量节点的选择时, 使由周期性确定的位置与即将填充的位置构成的矩阵能满足扩展后的校验矩阵的围长至少为6。同时, 所提构造方法的计算复杂度相对较低, 具有校验行数的3次方的复杂度。实验结果表明, 基于所提方法构造的QC-LDPC-C码对应基校验矩阵的扩展矩阵无4环, 并可获得较好的译码性能, 同时具有较低的编译码复杂度。另外, 所提的周期性比特填充方法也可用于其他卷积码的构造。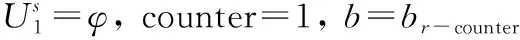






3 实验结果与讨论

4 结 语

