基于多模态低秩处理的沙漠地震随机噪声压制

张 珊, 李 月

(吉林大学 通信工程学院, 长春 130012)

0 引 言

随机噪声的存在大大降低了地震资料的信噪比, 为后续的构造成像和解释过程带来诸多不便。而且, 沙漠地带随机噪声的低频特性造成了有效信号和噪声的频带混叠, 使有效信号与噪声在频域较难分离。目前, 比较成熟的去噪算法多针对高斯噪声的压制, 而沙漠地带的随机噪声性质复杂, 并非都满足高斯分布, 因而这些成熟的方法对沙漠地带随机噪声的压制效果不理想。

近年来, 各国学者提出了一系列消减随机噪声的方法, 如f-x反褶积[1]、小波去噪[2]、 f-k滤波[3]、 Shearlet变换[4]和曲波阈值化[5]等, 文献[6-7]将非局部均值滤波应用于地震随机噪声压制。这些经典算法先后被应用于地震信号处理领域并取得了一定效果, 但在面临沙漠地震记录的复杂性时均表现出了明显的不足。面对能源地震勘探的“三高”要求、 复杂的地表和近地表地质条件、 深度不断加深和赋存空间越来越复杂的勘探目标, 常规地震数据去噪技术已逐渐难以满足当前高精度勘探的需求。

为寻求一种不受噪声性质和阈值限制, 足以应对强复杂随机噪声的去噪方法, 笔者将自适应噪声辅助的集合经验模态分解(CEEMDAN: Complete Ensemble Empirical Mode Decomposition with Adaptive Noise)算法[8]和ROSL(Robust Orthonormal Subspace Learning)低秩算法结合, 应用于沙漠地带随机噪声的消减。CEEMDAN分解算法[9]一定程度上克服了经验模态分解的模态混叠等问题, 广泛应用于医学信号和轴承故障检测, 并取得了较好的效果。单一的CEEMDAN算法虽可实现去噪目的, 但在降噪过程中需舍弃部分模态, 这大大削减了有效信号的保幅效果。ROSL低秩方法[10]面对噪声性质复杂多变的沙漠地震数据时, 单一的低秩并不能很好地分离有效信号和噪声。因此, 将二者融合, 既规避了沙漠地带随机噪声的低频和性质复杂而造成的常规方法不适用的问题, 又无需舍弃模态, 进而大大提高了有效信号的保幅效果。笔者将其应用于沙漠地震信号[11-12]处理, 对模拟和实际资料的处理表明, 其确实适用于沙漠地震信号的随机噪声压制。

1 随机噪声消减框架

在此框架下, 笔者选择CEEMDAN算法作为信号分解方法。CEEMDAN算法不依赖于噪声的性质和强度, 只需依据数据自身的尺度特征进行信号分解, 灵活度高且自适应性强, 非常适合非平稳非线性数据。在低秩方法上, 笔者选择ROSL算法[10]。ROSL算法适用于噪声更广泛的场景, 可处理更复杂的噪声, 进一步提高了模型的适用性。

1.1 CEEMDAN算法原理

CEEMDAN方法主要针对经验模态分解方法存在的模态混叠和虚假分量缺陷而设计, 该方法在特定的分解阶段加入特定频带的白噪声, 成功克服了实际应用中EEMD(Ensemble Empirical Mode Decomposition)[13-15]的虚假分量缺陷。

首先, 根据初始含噪信号的标准差σ, 决定构造集合信号的数量和添加白噪声的幅值； 然后, 对新构造的集合信号xi(t)=x(t)+Gi(t)进行EMD分解； 最后, 对每个集合信号的第1个IMF分量求集合平均, 得第1个IMF分量

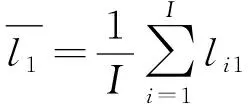
(1)

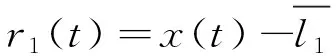
(2)

利用所得余量重新构造集合信号为r1(t)+ε1E1(Gi(t)),i=1,2,…,I, 并对该集合信号进行EMD[16-17]分解和集合平均运算得

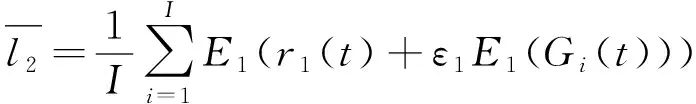
(3)

其中E1(·)为经过EMD方法筛选的第1个IMF模态分量,ε1为所添加噪声的系数。以此类推, 令集合平均次数k=2,3,…,K, 得第k个余量信号

(4)

进而求出第k+1个IMF模态分量

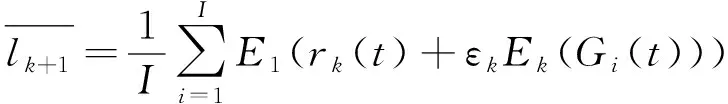
(5)

通过判定每个IMF分量是否符合固有模态函数的定义和性质, 决定该IMF分量是否为所需模态分量。若符合, 则输出, 否则返回重新进行结合平均运算, 得新的余量和模态分量后, 再进行新一轮判断。当余量信号rk(t)的极点小于3时, 不再分解,算法终止。最终的分解结果为

(6)

1.2 ROSL算法原理

类似于RPCA(Robust Principal Component Analysis), ROSL[18]假设观测矩阵X∈Rm×n由生成的低秩矩阵A(矩阵A的秩r≪min{m,n})和离群值稀疏矩阵E组成。不同于RPCA, ROSL利用一个普通的标准正交子空间下的低秩矩阵A=Dα, 其中D=[D1,D2,…,Dk]∈Rm×k, 系数α=[α1,α2,…,αk]∈Rk×n, 子空间的维度k=β1r,β1为大于1的常数。

(7)

在ROSL中, 结合了SVD(Singular Value Decomposition)的思想, 即令A=USVT, 子空间基于D=U和系数α=SVT。为保证计算效率, ROSL通过最小化‖α‖row-1和E的l1范数消除对α的正交约束, 以从X恢复低秩矩阵A, 即

(8)

1.3 沙漠地震记录噪声消减算法

设原始地震记录X={xij},i=1,…,N为采样点,j=1,…,B为道数。

1) 对原始地震记录进行CEEMDAN分解, 得到不同频带下的模态分量, 最终分解结果如式(5)所示, 每道地震数据均被分解出M个模态分量；

2) 将所有模态分量重新拼成一个新的N×MB维矩阵；

3) 利用ROSL算法, 对新矩阵进行低秩处理, 得稀疏和低秩两部分；

4) 将稀疏和低秩两矩阵中的每M列进行叠加, 得对应的两个N×B维矩阵, 其中稀疏部分叠加的矩阵为去噪结果。

2 仿真实验

2.1 模拟沙漠地震记录

为测试该方法降噪性能, 笔者将其用于处理一幅150道模拟地震记录。如图1所示, 每道记录600个采样点, 信号主频为25 Hz, 幅值均为1.0。由图1a和图1b可见, 信号的同相轴很大程度上被噪声淹没。对比图1c和图1d的传统降噪方法的处理结果, 在整体的压噪效果上, 笔者方法优于其他方法。小波和单一的ROSL算法虽也有一定的去噪效果, 但其噪声压制没有笔者算法彻底, 而且降噪处理后同相轴不够清晰连续。因此, 笔者算法对低频沙漠噪声具有较好的压制效果。

d ROSL算法去噪结果 e 笔者算法去噪结果图1 模拟记录Fig.1 Synthetic desert seismic record

为更直观对比几种去噪方法的保幅情况, 笔者给出了降噪后的差值记录与纯噪声记录的对比如图2所示。从图2中方框标出部分可见, 小波和ROSL算法都有明显的有效信号残留在差值记录中, 而笔者算法则几乎没有出现此问题, 小波去噪在弯轴部分有效信号存在明显残留, 而且对噪声压制也不彻底。因此, 在同等压噪效果的前提下, 笔者算法对有效信号的保留是最完整的。

通过以上实验对比可知, 笔者算法无论压噪效果还是有效信号的保幅效果都比较突出。表1定量给出了几种降噪方法降噪后的信噪比。由表1可见, 经笔者算法降噪处理后的信号信噪比提升最明显。由此, 笔者算法的优越性在时域上得以验证。

a 纯噪声信号 b 小波去噪差值结果

c ROSL去噪差值结果 d 本算法差值结果图2 差值结果Fig.2 Difference section

表1 信噪比

从频域角度出发, 整幅合成地震记录去噪后的频谱如图3所示, 差值信号的频谱如图4所示。观察图3c中标出区域可知, 小波变换对低频噪声的压制很不彻底, 同时还可发现, 对和有效信号混叠的噪声, 小波变换同样也无法很好地对其压制, 而且小波变换在去噪的过程中对有效信号存在明显伤害。同样, 由图3d方框区域可见, ROSL算法虽然对与有效信号混叠的噪声压制略有提升, 但整体低频噪声压制不彻底； 而从图3e可见, 笔者算法对低频噪声压制比较彻底, 同时几乎未造成信号的能量损失。

a 纯净信号频谱 b 含噪信号频谱 c 小波去噪结果频谱

d ROSL去噪结果频谱 e 笔者算法去噪结果频谱图3 合成地震记录频谱Fig.3 FK spectra of synthetic desert seismic record

图4进一步从频域的角度验证了算法的优越性。从图4中方框标出部分可见, 小波变换对有效信号和噪声混叠部分几乎没有压制效果, 同时造成了有效信号的能量损失； 而ROSL算法对噪声的压制并不彻底, 同时有效信号存在明显的能量损失。因此, 无论在时域或频域, 笔者算法在噪声压制和有效信号保持上具有一定优越性。

a 纯噪声频谱 b 小波去噪差值频谱

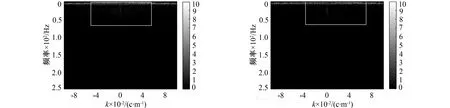
c ROSL算法去噪差值频谱 d 笔者算法去噪差值频谱图4 差值频谱Fig.4 The difference spectrum

2.2 实际地震记录

a 实际记录 b 小波处理结果

c ROSL处理结果 d 笔者算法处理结果图5 实际记录Fig.5 The processing results of real desert seismic record

图5为1幅每道1 800个采样点的实际共炮点记录及各算法的处理效果, 展示笔者算法的实际应用能力。由图5b可见, 小波变换虽对随机噪声起到了压制的效果, 但对面波的压制不彻底, 存在明显的噪声残留； 观察图5c中标出方框可以发现, ROSL算法同样存在面波压制不彻底的现象, 同时, 对随机噪声的压制效果也并不明显。而经笔者算法降噪后, 其同相轴清晰可见, 且足够连续, 说明笔者算法对有效信号的损失有限, 而且压噪效果明显。

3 结 语

针对低频沙漠地带随机噪声非平稳、 非线性等特性, 笔者将CEEMDAN算法和ROSL算法融合, 成功实现了对含有低频沙漠噪声的地震信号的噪声压制。一方面, 该方法灵活, 自适应性强； 另一方面, 较其他时频分析方法, 其拥有显著的特征识别效果。相比于单一的低秩算法, 与CEEMDAN的结合改善了由于频带混叠导致的低秩分解所得稀疏部分含有大量噪声的问题, 同时也解决了CEEMDAN算法分解后模态选取的难题, 无需舍弃模态的现状, 极大提高了沙漠地震数据降噪后的保幅效果。模拟记录处理结果表明, 与传统去噪算法相比, 笔者算法对沙漠地带的随机噪声具有很好的压制效果, 而且有效信号幅度衰减减小, 信噪比提升明显；实际地震记录的处理结果表明, 相比传统去噪算法, 笔者方法在降噪同时较好地保留了有效频率成分, 同相轴清晰可见, 连续性更好, 具有较好的实际应用能力。综上可得, 基于CEEMDAN和ROSL低秩算法的地震信号去噪方法实现简单, 能规避不利于降噪处理的信号特性, 具有较好的使用价值。