基于双目立体视觉的标定技术及应用
田 昊, 刘春萌
(东北石油大学 电气信息工程学院, 黑龙江 大庆 163318)
0 引 言
目前, 三维视觉正在呈井喷式发展, 并在计算机视觉会议CVPR(International Conference on Computer Vision and Pattern Recognition)、 ICCV(International Conference on Computer Vision)、 ECCV(European Conference on Computer Vision)中, 三维视觉相关论文比例逐年上升, 达到了30%以上; 同时三维视觉技术被广泛应用于智能无人系统, 如无人车、 无人机和机器人[1-3]、 增强现实[4]、 城市建设、 遥感制图[5]和娱乐等方面, 并且进一步推动了该技术的发展。在三维视觉领域中, 双目视觉是不可或缺的重要部分。在工业领域中, 自动化检测代替人工检测是必然趋势, 双目视觉也在逐步发展, 并且其需求也越来越广泛。开始双目视觉只用于生产线上, 而目前, 其在制造、 医疗和仓储等各个领域都有广泛应用。由于工业上基本以三维部件为主, 且二维成像毕竟是来自三维空间实际情况的一种不完全数据采集, 所以目前围绕3D的各种检测、 测量和机器人引导等[6]研究层出不穷。
在用摄像头感知世界时, 标定准确的单目、 双目、 甚至多目系统是得到准确信息必要条件。按照标定方式, 单目相机的标定主要有两大类: 主动视觉标定和相机自标定。前者利用已知参数标定板, 在相机成像视野里做X、Y、Z旋转, 从不同角度对标定板进行拍摄。关于相机自标定, 存在许多经典研究。Hartley[7]提出一种针对空间任意一点, 在相机自身旋转拍摄图片后实现相机自标定的方法; Ma[8]提出的方法不需要已知特殊标识点, 而且能线性求解标定参数; Moons等[9]提出以相机的平移量为变量进行拍摄, 从两幅图像上的6个标识点就可得出相机参数的方法。Faugera等[10]提出的自标定思想可在不需要标定板和相机固定位置运动的情况下对相机参数进行标定, 同时给出任意两幅图之间的约束关系, 并且利用Kruppa求解, 但计算量很大; Triggs[11]提出绝对二次曲线的方法, 利用数学函数及相关几何关系定理求解。双目标定的研究方向主要有两个[12]: 一个是对标定板的创新, 如利用棋盘格的、 圆形列阵和三维立体标靶等; 另一个是对数据处理方法的研究, 如用自适应阈值分割并采取最小二乘法拟合椭圆, 利用图像整体信息构建目标函数优化标定参数, 以及用三点成圆并逐点计算径向误差值, 而利用径向误差约束、 粒子群优化算法和最小二乘法的非线性隐式标定法有收敛速度快泛化能力强的优点。随着研究的不断深入, 改进的粒子群算法, 遗传算法也不断得到应用[13]。
笔者在结合双目立体视觉的基础上, 对立体视觉进行标定。首先依靠基于小孔成像的双目成像模型作为标定过程中数据点转换模型, 同时也有标定板对应的模型; 然后为了能有效提取感兴趣区域, 在模型正确建立前提下, 对获取图像做二值化、 灰度化、 边缘提取、 形状选择等基本操作; 最后对标定板做精确选中, 为标定数据提取奠定基础。
1 相机标定基本原理
1.1 标定目的
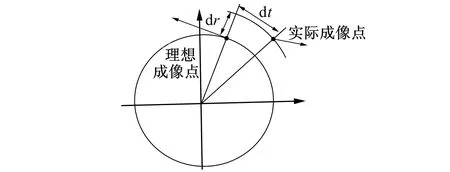
图1 镜头畸变示意图Fig.1 Lens distortion diagram
相机镜头透镜的弯曲必然导致折射现象, 从而产生畸变。然而, 在实际应用中, 弯曲镜头是首选。因为在针孔模型中, 针孔很小, 进而透过的光线很少, 造成在现实使用时曝光不足, 使图像生成速度缓慢。为快速生成清晰图像, 必须使用面积大而弯曲的透镜, 使足够多的光收敛汇聚到投影点上。这样做的代价是引入了镜头畸变。如图1所示, 透镜畸变导致理想成像点和实际成像点不在同一位置, 其中dr为径向畸变, dt为切向畸变。越靠近透镜中心的位置, 畸变越小; 越靠近边缘处, 畸变越大。因此, 使用相机之前对其标定是十分必要的。
1.2 坐标转换
在图像测量、 定位过程以及其他机器视觉应用中, 为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系, 必须建立相机成像的几何模型。这些几何模型参数就是相机参数, 而求解参数的过程即为相机标定。因此求解出镜头的畸变参数, 就可以把有畸变的图像变换到没有畸变状态的图像。
1.2.1 从世界坐标系到相机坐标系
空间点PW(XW,YW,ZW)与转换点P(XC,YC,ZC)之间的关系式为
P=RPW+T
(1)
其中R是旋转矩阵,T是平移矩阵。
每个世界坐标系的对象都可通过旋转和平移变换到相机坐标系上。由X-Y坐标系统向X′-Y′坐标系统的转换如图2所示, 将目标点旋转θ, 等价于将坐标系按相反方向旋转θ。图2是二维坐标的旋转变换, 而对于三维坐标, 绕某个轴旋转的原理与二维坐标旋转相同, 整体的旋转矩阵由3个轴的旋转矩阵相乘构成。

图2 坐标旋转原理Fig.2 Principle of coordinate rotation
利用极坐标变换得到图2所示两个坐标系统的旋转变换为

(2)
如果世界坐标分别绕X、Y和Z轴旋转α、β、γ, 则旋转矩阵R(α)、R(β)、R(γ)分别为

(3)

(4)
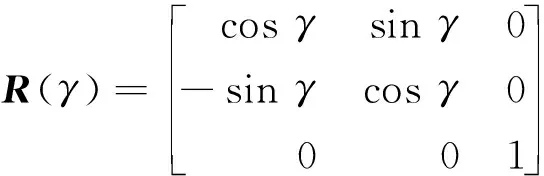
(5)
总的旋转矩阵
R(α,β,γ)=R(α)R(β)R(γ)
(6)
1.2.2 从相机坐标系到图像坐标系
图3是从相机坐标系到图像成像坐标系的一种投影变换关系, 结果将3D图像信息转换成2D图像信息。其中点P(XC,YC,ZC)是相机坐标系中的一个点, 点p(x,y)是点P(XC,YC,ZC)在图像坐标系上的投影。其中OC-XCYCZC为相机坐标系, 光心为原点, 单位: m;O-xy为图像坐标系, 光心为图像中点, 单位: mm;u-v为像素坐标系, 原点为图像左上角, 单位: pixel。P为世界坐标系中的一个点, 即生活中真实存在的一个点;p是P在图像中的成像点, 在图像坐标系中的坐标为(x,y), 在像素坐标系中的坐标为(u,v),f=‖O-OC‖为相机焦距。

图3 相机成像坐标系变换原理图Fig.3 Schematic diagram of camera imagingcoordinate system transformation
从图3可知: ΔABOC~ΔOCOC, ΔPBOC~ΔpCOC。
利用相似三角形比例关系, 有

(7)
从而, 可得

(8)
进而, 可得坐标转换矩阵

(9)
1.2.3 从图像成像坐标系到图像像素坐标系
图像像素坐标系u-v是以图像左上角为原点, 以图像互为直角的两个边缘为坐标轴, 满足右手准则。图像由许多小像素点组成, 并且像素坐标系的横纵坐标以像素点为单位, 描述每个像素点在图像中的位置, 而成像坐标系是以光轴与像平面交点为原点建立的。如图4所示的图像成像坐标系是以mm为单位的直角坐标系x-y。
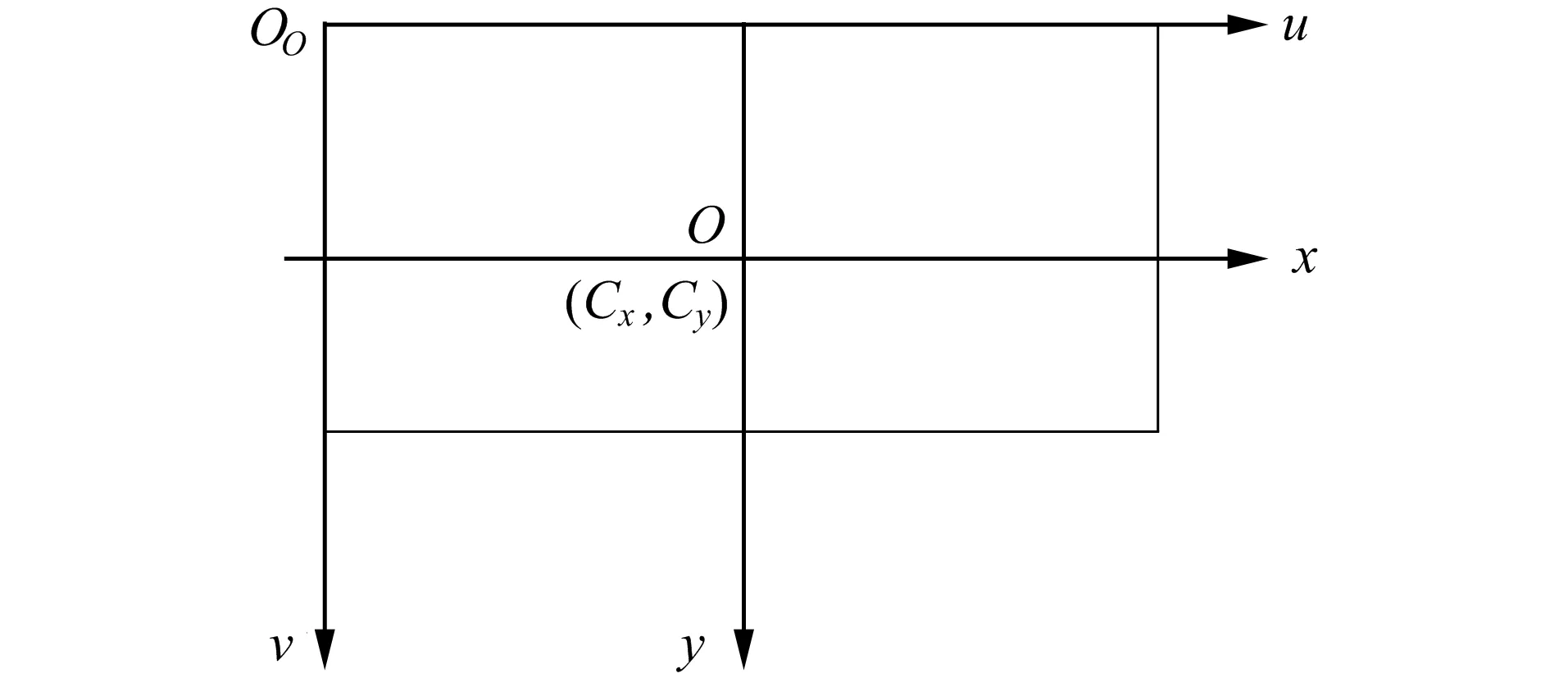
图4 像素坐标系和图像成像坐标系Fig.4 Pixel coordinate system and imaging coordinate system
用(u,v)描述图像像素坐标系中的点, 用(x,y)描述图像成像坐标系中的点。成像坐标系的原点O在像素坐标系中的坐标为(Cx,Cy), 用dx,dy表示相邻像素点中心在x轴方向和y轴方向的实际物理距离, 则其与像素坐标系的转化关系为

(10)
转换为矩阵

(11)
2 双目标定
2.1 标识点坐标获取
对边缘进行特征处理后, 得到标志点在相机坐标系下的坐标。再主要依据聚类的思想, 对边缘点做处理。拟合边缘点, 得出每个圆形边缘的方程, 进而确定其圆心, 最终求得坐标。
根据圆上3个点可确定一个圆, 引入径向误差作为约束条件, 通过设置阈值, 排除或留下边缘上的点。初选3个点, 求出半径和圆心并计算径向误差, 若满足, 则留下; 若不满足, 则去除; 循环取点, 以此类推, 直到全部处理完毕为止。将选出的点进行最小二乘拟合, 带入拟合方程后就可得到圆心。
从边界上顺序取出不在一条线的3个点A(uA,vA)、B(uB,vB)、C(uC,vC), 由几何原理知能确定一个外接圆, 以(u0,v0)为圆心
(uA-u0)2+(vA-v0)2=(uB-u0)2+(vB-v0)2
(12)
(uA-u0)2+(vA-v0)2=(uC-u0)2+(vC-v0)2
(13)
根据克拉默法则求解, 得
在实际相机使用过程中, 当光透过透镜时, 特别是在远离光心的位置会有较大畸变。因此, 需进行相机的畸变矫正。工业相机镜头自身对相机畸变有一些物理上的处理, 因此主要考虑径向畸变(见图1), 模型如下。
定义径向误差
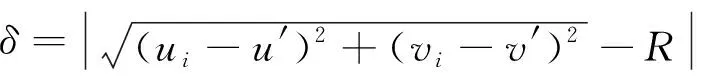
(16)
保留满足该条件的点, 每次取3个点求解圆和径向误差; 若不满足, 则以前两个点为基础另取一点计算。以此类推, 完成全部遍历。
将经上述处理的点以最小二乘法拟合圆心。设边界点数据为(xi,yi)(i=1,2,3,…,n), 则对应圆的方程为
(x-x0)2+(y-y0)2=R2
(17)


(18)
求解出的x0,y0是各个标志点在像素坐标系中的位置, 根据上述坐标系之间的转换关系可将该像素坐标直接与世界坐标建立联系。由式(6)、 式(9)和式(11)联立, 可得

(19)
其中M1为内参矩阵, 由相机的焦距、 像元大小等构成;M2为外参矩阵, 由左右相机之间的旋转和平移矩阵构成。平移矩阵t=(tx,ty,tz)T,tx、ty、tz是世界坐标系原点与相机坐标系目标点之间的差值。
式(19)进一步简化为
sI=M34P
(20)
其中s是可求解的不确定因子;M34是内参矩阵和外参矩阵的乘积, 也即投影矩阵;P=(Xw,Yw,Zw,1)T为增广矩阵。
2.2 单应性矩阵求取
单应性变换的实质是描述物体在世界坐标系和像素坐标系之间的位置映射关系, 将该映射之间的变换矩阵称为单应性矩阵。单应性矩阵定义为

(21)

由式(20)可知
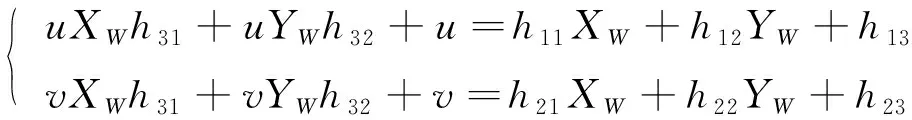
(22)
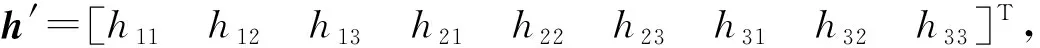

(23)
将标定板上标识点的世界坐标值以及图像坐标值带入式(23), 利用最小二乘法求出h′, 进一步求出单应性矩阵H。
2.3 内参求解
由图2可知, 坐标轴之间保持正交性, 因此, 各轴平面内的旋转角度α和β也是正交向量, 所以有约束方程

(24)


(25)
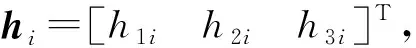
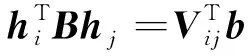
(26)
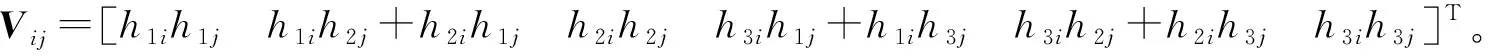
将约束方程写成关于b的形式
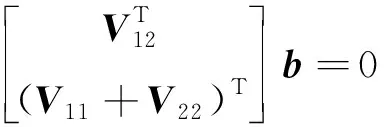
(27)
在相机得到n幅不同位姿图像的情况下, 将有n个式(24)方程, 联立得
Vb=0
(28)
其中V是2n×6矩阵。
在理论上, 利用最多5幅图像的数据就可求解出向量b。因此, 分别求取相机的内参

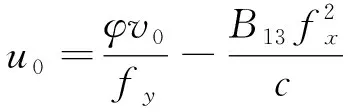
(29)
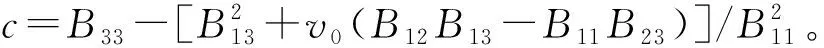
2.4 外参求解
将相机的内参和单应性矩阵带入式(21), 可得对应的外部参数[14]
r1=λA-1h1,r2=λA-1h2,r3=λr1r2,t=λA-1h3
(30)

3 双目标定实现
在双目标定的过程中采用以下几个步骤。首先, 读取标定板左右双目的多组图片, 如图5所示; 然后, 在左右图像中基于标定板描述文件以及边缘等处理, 选出感兴趣区域, 并获取标定板上标识点的坐标, 如图6所示; 最后, 利用式(29)、 式(30)求解出相机的内外部参数。

图5 选中标定板区域 图6 选中标识点中心 Fig.5 Check the calibration board area Fig.6 Select the center of the identity point
表1和表2为一组标定板在左右相机成像平面上的图像坐标, 准确获取该数据为进一步标定打下基础。
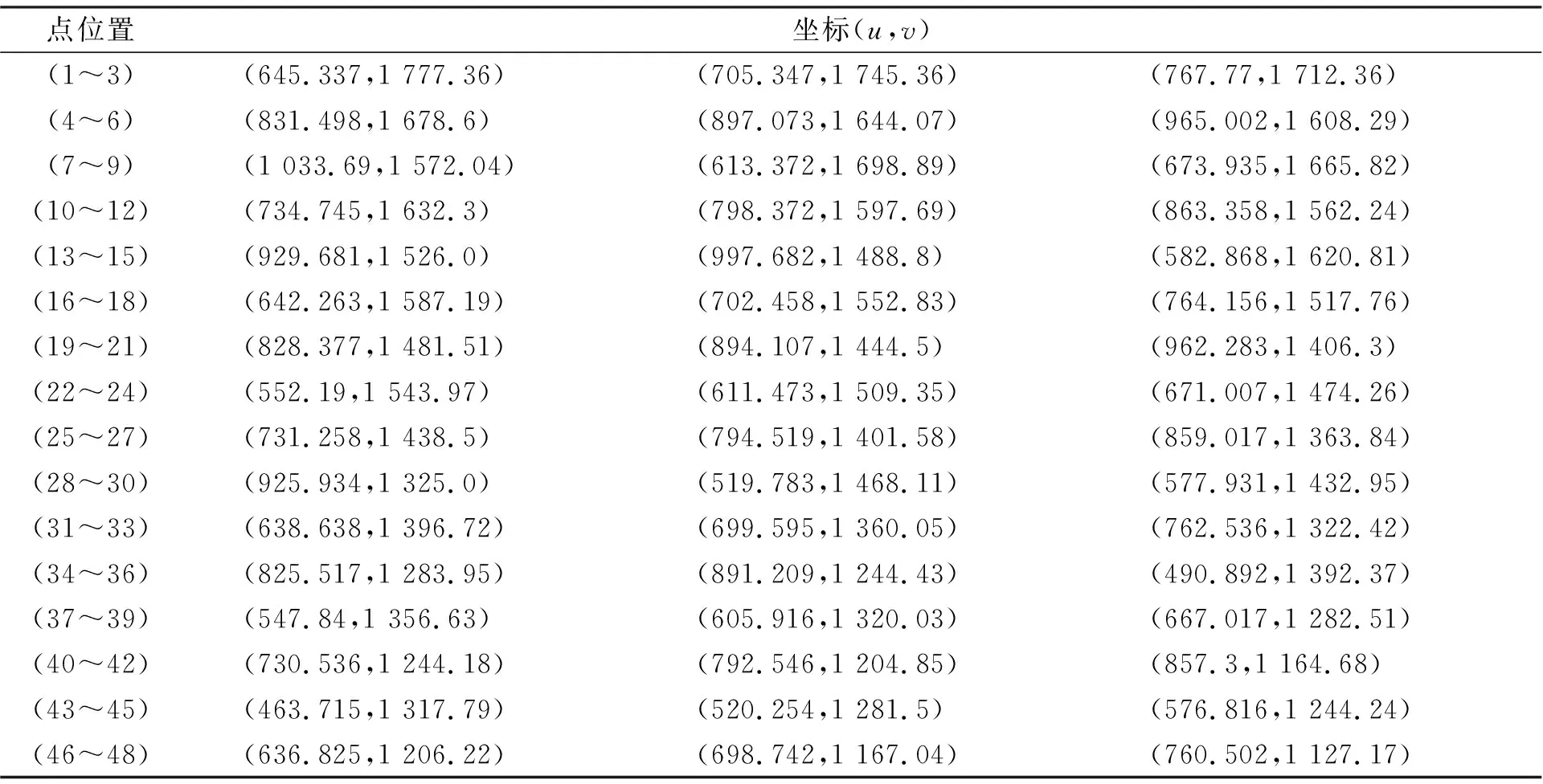
表1 左相机标识点坐标

表2 右相机标识点坐标
如表3所示, 左右相机的参数并不完全相同, 根据双目立体成像系统的定义, 这并不是理想的双目系统。这也是要进行双目标定的原因, 通过标定可使其成为接近理想的状态, 矫正后相机内参如表4所示。

表3 相机内参

表4 矫正后相机内参
表5是矫正后的相机内参。由于笔者主要做标定工作, 对矫正不做过多解释, 在此仅陈列标定结果。由表5可见左右相机在世界坐标系的位置, 其相互之间的位置也是已知的, 这就是双目立体成像系统中所要求解的相机外部参数。

表5 左右相机初始位姿
表6为左右相机矫正位姿参数。由表6可见, 对相机位姿的调整, 主要是旋转角度的调整。表6所示为左右相机所需要调整的参考调整数据, 这有利于构建理想的相互平行的双目系统。

表6 左右相机矫正位姿
表7为左相机相对右相机位姿参数。由表7可见, 即使专业的双目立体成像系统, 其左右相机位置也不是十分理想, 在Y轴和Z轴上分别有7.4 mm和5.8 mm的偏差, 同时也存在一定旋转。

表7 左相机相对右相机位姿
表8为矫正后左相机对右相机的点变换。由表8标定结果可知, 左右相机的光轴相距1.629 15 m, 在XYZ轴上均无旋转,YZ轴上也无平移。

表8 矫正后左相机对右相机的点变换
4 结 语
在双目相机姿位、 焦距固定的条件下, 笔者通过选择标定板, 标定板图像预处理, 提取标识点坐标, 根据计算公式进行双目标定, 求解出双目两个相机的内参和外参。结合应用过程, 与实际双目视觉装置比较, 确定该方法具有良好的精度, 为该双目立体视觉系统对数据的获取提供了精确的数据基础和可靠的矫正条件。

