基于二维DCT的鬼成像高效目标重构
赵 群, 桑爱军, 栾晓利, 赵 岩, 贾姗姗
(1. 吉林大学 通信工程学院, 长春 130012; 2. 空军通信士官学校 对空通信系, 辽宁 大连 116600;3. 空军航空大学 初级训练基地, 长春 130022; 4. 长春大学 理学院, 长春 130022)
0 引 言
鬼成像也称关联成像, 作为一种新的成像技术, 实现了将图像的探测与成像过程的分离, 从而可以在更复杂的环境下实现成像。关联成像最初被认为是只有当光源为纠缠光时才能通过二阶关联运算得出目标的信息。随后, 研究者通过实验得出赝热光也可以作为关联成像光源并通过优化光场等物理方法提高成像质量[1]。但是, 关联成像中的二阶关联恢复算法依然是沿用传统的香农采样定理的框架, 其通过大量测量恢复目标图像的方式, 虽然降低了噪声的影响, 但大大增加了计算时间[2-4], 系统的实时性受到了严重的制约。采用Hadamard矩阵作为测量矩阵, 利用矩阵的任意两列(两行)的不相关性, 理论上可实现图像的近百分之百的重建[5]。但由于Hadamard矩阵的特点制约了成像效率, 将实时视频的应用限制在相对较低的分辨率上[6]。压缩感知可以解决低分辨率和欠采样问题[7-8], 但需要大量学习训练准备。之后有人提出了基于沃尔什矢量变换方案的单像素成像, 采样次数占全部采样的20%时也能得到清晰的重建图像[9]。由于鬼成像在雷达改进[10]、 大气条件参数获取[11]和空间望远镜[12]等方面有广泛应用, 因此研究更先进的信号处理方法一直是关联成像技术的主要问题。笔者提出了一种新的基于二维DCT欠采样鬼成像高效目标重构方法, 从而进一步降低采样次数而获得清晰的重构结果。
1 二维DCT鬼成像目标重构模型
1.1 一维Hadamard变换、 一维与二维DCT
长度为N的列矩阵f的一维离散变换的矩阵表示形式为
FN×1=ΦNfN×1
(1)
其中当ΦN表示N阶Hadamard矩阵时, 式(1)代表一维Hadamard变换; 其核为

(2)
其中bk(z)是z的二进制表达的第k位,N是Hadamard变换的阶数,N=2n,u=0,1,2,…,N-1,x=0,1,2,…,N-1。
从形式上看, 离散余弦是线性的可逆函数:F:Rn→Rn, 其中R是实数集, 或等价于一个n×n的方阵, 实质是将n个实数x0,…,xn-1变换到另外n个实数c0,…,cn-1的操作。如果k代表对应实数的序号, 则反映一维DCT原理的公式为[12-15]

(3)


(4)
则C(k)即为经转换后的值。
对于二维DCT方法, 其公式如下

(5)

另外, 定义二维逆离散余弦变换(IDCT: Inverse Discrete Cosine Transform)的公式为

(6)
1.2 二维DCT鬼成像理论分析
二维DCT变换有两种等价矩阵形式, 具体可由
表示。其中⊗代表克罗尼克乘积。
为实现二维DCT变换的鬼成像, 首先产生一个N2阶的二维DCT矩阵CN2×N2, 该矩阵每行重新排列后得到方阵I(x,y)作为测量矩阵,I(x,y)照射到目标物体O(x,y)后, 得到桶探测值B。CN2×N2的第i行与得到的第i个桶探测值的关系如下

(9)
其中O=[O(1,1),O(1,2),…,O(N,N)]T是目标物体O(x,y)的一维表示形式,i=1,2,3,…,N2。矩阵CN2×N2共有N2行, 可得到N2个桶探测值, 以列矩阵的形式表示

(10)

(11)
其中BN×N是鬼成像中桶探测值列矩阵的二维表示形式。利用式(11)即可通过对桶探测值矩阵进行二维DCT重构得出目标图像,算法实现流程如图1所示。

图1 二维DCT鬼成像目标重构实现流程Fig.1 Realization process of 2D DCT ghost imaging target reconstruction
2 数值仿真
根据上述理论分析, 一维与二维Hadamard变换效果相同。下面分别对基于一维与二维Hadamard变换的鬼成像(1D_HTI, 2D-HTI: Ghost Imaging based on One-Dimensional Hadamard transform)及基于一维与二维DCT的鬼成像(1D_DCTI, 2D_DCTI: Ghost Imaging based on Tow-Dimensional DCT)进行数值仿真。数值模拟仿真使用Matlab软件实现, 采用大小为64×64像素的Cameramen二值目标图(JLU)和多灰度图(辣椒)作为目标物体, 仿真过程如图1所示, 结果如图2所示, 对目标图像进行相应的正交变换得到相应的桶探测值矩阵如图3所示。
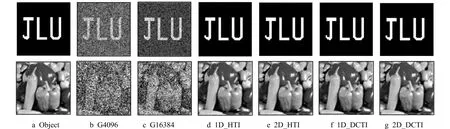
图2 鬼成像算法仿真对比图Fig.2 Ghost imaging algorithm simulation comparison diagram

图3 桶探测值区域能量集中性对比图Fig.3 Contrast diagram of energy concentration in bucket detection area
从图2可看出, 高斯无论是4 096次还是4倍的16 384次仿真重构得到的结果都无法实现百分百重构, 理论上后4种变换4 096次照射可以完全恢复目标物体。从图3中可以看出, 这4种变换对图像具有不同程度的能量集中效果, 即桶探测值矩阵的能量分布不同, 图3a、 图3b中能量呈随机分布, 图3c、 图3d中能量分别向左侧和左上集中。
DCT是傅里叶变换的对称扩展形式, 符合傅里叶变换从低频到高频的特性, 图像的能量向低频区域集中。一维DCT去除了列之间的相关性, 所以变换后能量向左侧集中, 如图3c所示。对比图3, 得出二维DCT能量集中性效果最好, 它能同时去除目标图像行、 列的相关性, 能量向左上角集中, 如图3d所示。选择桶探测值矩阵左上角区域方法如图4a所示, 求出其能量集中率(EPE: Energy Packing Efficiency,EEPE)
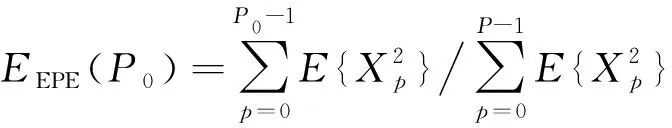
(12)
以度量图4b该区域的能量集中性[9]。从图4b中可以得出, 桶探测值能量集中性方面二维DCT优于一维, 一维DCT优于二维和一维Hadamard, 二维和一维Hadamard能量集中性相同。
图像质量利用峰值信噪比(RPSNR)进行衡量, 定义为

(13)
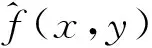

a 欠采样取值图 b 桶探测值能量集中性对比图 c 重构结果PSNR曲线对比图图4 能量集中性对比图Fig.4 Energy concentration contrast diagram
由图3d可以看出, 2D_DCTI桶探测值图像的能量向低频区域集中, 该区域包含图像大量的轮廓信息。所以选取桶探测值矩阵左上角的部分数据, 优先实现图像重构。分别对1D_HTI, 2D_HTI, 1D_DCTI和2D_DCTI进行二值目标物和多灰度目标物的欠采样仿真对比, 按照从左上角到右下角的顺序进行采样, 对未选中桶探测值位置置0处理。结果如表1所示, 采样率代表选择的部分数据占全部数据的百分比。从表1可看出, 采样数逐渐递增时, 2D_DCTI的重构结果先得到图像的轮廓信息, 再逐渐得到图像的细节信息。由表1可知, 在采样点数相同的情况下, 2D_DCTI的成像质量优于1D_DCTI,1D_DCTI的成像质量优于1D_HTI, 1D_HTI与2D_HTI效果相同。

表1 重构结果欠采样仿真对比表
3 实验结果与分析
图5为基于二维DCT鬼成像目标重构实验装置。对大小为64×64像素的二值图像(JLU)和多灰度图像(辣椒)进行目标图像重构。
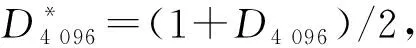
测量矩阵经投影仪调制后照射到目标物体, 照射光场经由物体反射后由桶探测器接收, 获得桶探测值。通过关联公式, 进行图像重构。为了对比, 分别以高斯散斑、Hadamard和DCT矩阵作为测量矩阵, (仿真时1D_HTI与2D_HTI效果相同, 实验中略去2D_HTI), 进行相同照射次数的实验, 并增加一组16 384次高斯实验对比观察试验结果。实验中通过桶探测值差分减小环境噪声的影响[9], 利用该矩阵完成图像重构。对二值目标物和多灰度目标物重构结果分别进行中值滤波拉伸和直方图均衡化处理, 实现进一步去噪。根据3种方法得到的实验结果如表2所示。

a 实验装置示意图 b 主要实验设备图5 鬼成像目标重构实验装置图Fig.5 Experimental device for ghost imaging target reconstruction

表2 鬼成像目标重构对比表
由表2可以看出, 采用相同图像增强技术后, 2D_DCTI的实验结果最好。下面通过实验验证不同欠采样取值时目标物体重构效果, 其中二值目标物JLU直接进行鬼成像重构及欠采样处理, 多灰度目标物辣椒, 对鬼成像结果做图像增强后进行欠采样处理, 如表3所示。

表3 欠采样实验对比表
对比表3的二值和多灰度图像欠采样重构结果可以发现: 无论是否使用图像增强, 相同采样点数下, 2D_DCTI在采样率12.5%可清晰看出成像内容为“JLU”和“辣椒”, 在采样率6.25%可判断出成像内容为“JLU”和“辣椒”, 而1D_HTI与1D_DCTI在采样数较少时, 存在严重的重影和失真现象, 几乎无法识别图像信息。在图像重构中, 主要的计算量来源于相应的正交变换, 2D_DCTI通过对新的桶探测值矩阵左右同时乘以相同大小的一维DCT逆矩阵和矩阵完成二维DCT变换。
4 结 语
笔者提出基于二维DCT高效鬼成像方案。通过实验验证, 在相同采样数下, 2D_DCTI的重构质量与1D_DCTI和1D_HTI、 2D_HTI相比具有绝对优势, 在采样率为12.5%时可获得图像的基本信息。根据二维DCT的能量集中性, 选择理论上能量高的桶探测值对应的矩阵作为测量矩阵, 在满足重建图像质量的前提下, 可减少采样次数。该成像方案可在较低的采样率下快速获得图像的基本信息, 判断出图像所要表达的基本内容, 在军事雷达、 航空航天等有关目标识别的领域均有广阔的应用前景。

