降低OFDM系统峰均功率比的改进算法
张秀艳, 何润霖
(东北石油大学 电气信息工程学院, 黑龙江 大庆 163318)
0 引 言
正交频分复用也称为OFDM(Orthogonal Frequency Division Multiplexing)[1-4]技术,它是从多载波调制技术上发展起来的, 由于该技术优点突出, 发展迅速, 能产生不同种类的演变技术, 因此很受欢迎。其优点有抗窄带干扰性强, 能最大限度的利用频谱资源, 抗多径衰落强等。但该技术的缺点是峰均功率比(PAPR: Peak Average Power Ratio)高, 因此会增加系统的运营成本, 降低放大器的工作效率, 严重影响系统的实际应用。国内外学者对降低PAPR的方法进行大量研究, 其中复杂度最低的是预畸变类技术, 该技术不仅与概率类技术中的选择映射技术(SLM: Selective Mapping)[5-7]、 部分传输序列技术(PTS: Partial Transmit Sequence)[8-11]相同都要传输边带信息, 而且也不会像编码类技术中的分组编码(Block Code)[12]和Turbo编码[13-14]受调制方式和子载波数目影响, 但很容易产生限幅噪声, 其代表为限幅法(Clipping)[15-16]和窗函数法(Window Method)以及星座图扩展法[17-19]。笔者研究的是预畸变类技术中的凸集映射星座图扩展法(ACE-POCS)[20]。由于ACE-POCS方法收敛速度较慢, 达到理想效果要相当多的迭代次数, 增加了计算的时间复杂度, 因此算法的效率较低。在不降低误码率性能的情况下, 为了尽可能的改变这种情况, 笔者提出LS-ACE-POCS算法, 即采用最小二乘估计法算出一个最优因子, 把最优因子与消峰信号相乘后的结果与原始噪声最佳逼近, 因此一次迭代便可达到理想效果。
1 LS-ACE-POCS算法
1.1 传统ACE算法原理
传统ACE算法是通过扩展外围星座点优化系统的PAPR, 实现扩展的方式是在ACE处理前的信号上叠加若干个正余弦信号, 因此处理后的信号和处理前的信号在幅度和相位上有很大差别, 从而大多数子载波在某一点上有相同或相似的相位的可能性会大大降低, 减少了发射机和接收机的设计难度, 降低信号发生畸变的可能性, 确保误码率不会恶化。由于边缘星座点畸变到星座图的外围, 使ACE扩展后的星座点的欧氏距离变大, 因此在接收端接收到的错误码元数目会减少。该算法可以用数学表达式表示为

(1)
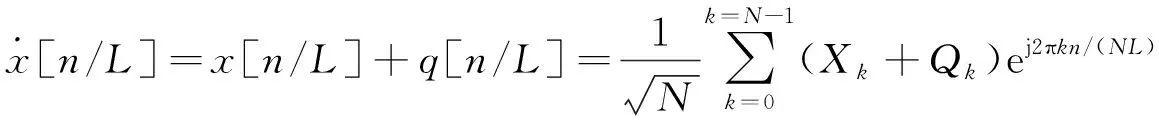
(2)

1.2 ACE-POCS算法原理
由于该过程求解非常困难, 于是采用凸集映射星座图扩阈值展法。设时域阈值为A, PAPR阈值为PPAPRTh, 最大迭代次数为Im两个凸集分别为RA和RE,RA信号满足时域信号在阈值A以下,RB信号满足ACE约束条件, 两个凸集有一个相交区域, 这个相交域里可获得理想解, 设定信号先经过RA后经过RB为一次迭代过程, 通过不断地迭代, 信号会逐渐靠近理想解。这个过程可以理解为: 通过快速傅里叶逆变换(IFFT: Inverse Fast Fourier Transform)运算将频域数据变换为时域的x信号, 再进行如下操作
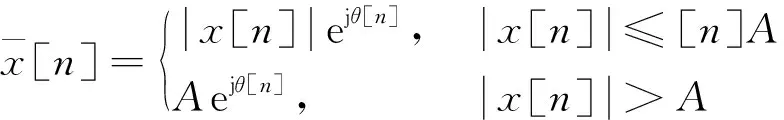
(3)

1.3 LS-ACE-POCS算法的原理
笔者提出的LS-ACE-POCS算法, LS的原理是将残差平方和的总和最小化, 因此用在求最优因子中是非常优越的, 图1展示了新算法的框图。

图1 LS-ACE-POCS算法实现框图Fig.1 Implementation diagram of LS-ACE-POCS algorithm
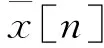
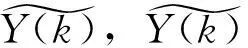

(5)
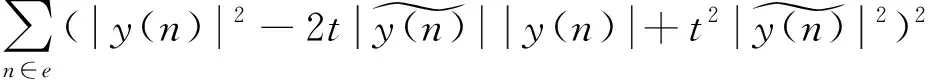
(6)
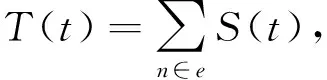

(7)
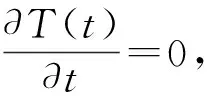

(8)

(9)

2 LS-ACE-POCS算法的PAPR性能分析
设第l个OFDM符号的时域表达式
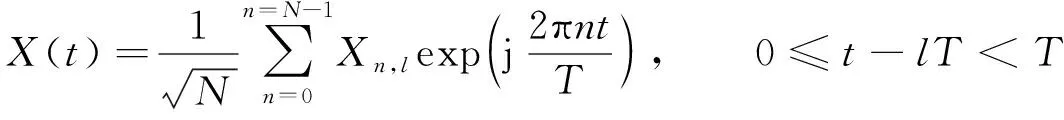
(10)
其中N是子载波数目,T是符号周期,Xn,l是第l个符号在第n个子载波上的数据。
第l个符号的峰均功率比表达式是

(11)
互补累积分布曲线(CCDF: Complementary Cumulative Distribution Function)能准确描述PAPR的概率分布, CCDF是指超过某一阈值的概率, 数学表达式为
P(RPAPR>RPAPRTh)=1-(1-e-RPAPRTh)N
(12)
2.1 同一参数下不同方法结果比较
当限幅阈值A=1.923, 子载波数N=512, 采用QPSK调制, 仿真原始信号、 采用ACE-POCS算法和LS-ACE-POCS算法的PAPR统计分布比较如图2所示, ACE-POCS算法最大迭代次数ImACE=10, LS-ACE-POCS算法的最大迭代次数ImLS-ACE=1。
由图2可知, 原始信号的RPAPR=10.695 dB, 采用ACE-POCS算法第1次迭代RPAPR=9.183 dB, 仅一次迭代PAPR就下降了1.512 dB, 第2次迭代PAPR降到8.367 dB, 与第1次相比降低了0.816 dB, 随着迭代次数的增加, 迭代力度越来越小, 第10次迭代降为6.207 dB。采用LS-ACE-POCS算法第1次迭代就达到5.984 dB, 比ACE-POCS算法第10次迭代还低0.223 dB, 因此降低PAPR能力非常优异。
2.2 阈值A对实验结果的影响
由于不同的限幅阈值对实验结果有影响, 因此要选择最佳阈值。阈值A通过公式:A=sqrt(10(10*log10(原始信号能量的平均值+m)/10))选择, 本次仿真m从3.68~6.68选取, 分别得到A为1.527 6、1.714 0、1.923 1、2.157 7, OFDM符号是1 000个, 采用QPSK调制, 子载波数为256, PAPR阈值(PAPRTh)是6 dB, LS-ACE算法最大迭代次数ImLS-ACE=1次, 得到仿真如图3所示。

图2 不同算法降PAPR能力对比图 图3 不同阈值降PAPR能力对比图 Fig.2 Contrast diagram of PAPR reduction Fig.3 Contrast chart of PAPR reduction ability of different algorithms ability with different threshold values
从图3中可以看出, 当A=1.923的RPAPR为6.097,A=1.714的RPAPR为6.252,A=2.158的RPAPR为6.77,A=1.528的RPAPR为6.909。可见当阈值A=1.923时, PAPR最低, 最接近RPAPRTh。
2.3 子载波数对实验结果的影响
由于不同的子载波对实验结果有影响, 为了研究子载波数目如何影响PAPR降低能力, 本次仿真采用不同的子载波数目在QPSK调制下并且限幅阈值A=1.923,RPAPRTh=6 dB, 得到实验仿真如图4所示。
由Matlab仿真结果可知, 原始信号N=64、N=128、N=256、N=512的RPAPR分别是11.095、6.854、6.627、6.171、5.988(dB)。可见笔者算法在N=512时降低PAPR能力最强,N=64时最弱, 这是因为星座点扩展的数目与仿真的子载波数目成正比, 降低PAPR能力与星座点扩展的数目亦成正比。
2.4 调制方式对实验结果的影响
为了研究调制方式对PAPR降低能力的影响, 在此采用未经调制、 经QPSK调制、 16QAM调制、 64QAM调制的信号进行仿真, 预先设定阈值A=1.923, 子载波数N=512, PAPR阈值是6 dB,ImLS-ACE=1, 得到仿真结果如图5所示。

图4 不同子载波PAPR对比图 图5 不同调制方式对PAPR性能的影响 Fig.4 Comparison diagram of PAPR Fig.5 The influence of different modulation of different subcarriers modes on PAPR performance
从Matlab仿真可知, 原始信号的RPAPR是11.054 dB、采用64QAM调制的RPAPR是8.792 dB、 采用16QAM调制的RPAPR是7.664 dB、 采用QPSK调制的RPAPR是5.974 dB。可见采用QPSK调制方式最好, 采用64QAM调制方式最差, 但都比原始信号有更强的降低PAPR能力, 我们可以得出结论: 调制方式越高, 降低PAPR性能越低。
3 LS-ACE-POCS算法的BER性能分析
3.1 误码率的产生
误码率能度量数据在系统传输中是否准确。由于信号在传输过程中受到噪声和不同调制方式、 算法、 通信系统组成部分质量不够理想等因素的影响从而导致信号在接收端无法完全正确地被接收, 这样就产生了误码率。
3.2 误码率的仿真结果
该仿真手动生成高斯白噪声信号, 仿真环境是高斯白噪声信道(WGN: White Gaussian Noise), 仿真信号的信噪比(SNR: Signal Noise Ratio)在0 ~12 dB之间。仿真16QAM和QPSK调制下3种信号的误码率。从图6中明显可以看出, 采用16QAM调制的误码率比采用QPSK调制的误码率高很多, 并且16QAM调制下原始信号、 ACE-POCS算法、 LS-ACE-POCS算法误码率几乎近似。由Matlab仿真可知, 在SNR=12 dB处, 原始信号、 ACE-POCS算法调制、 LS-ACE-POCS算法调制的BER分别是0.028 3、0.027 5、0.027 1(dB)。但采用QPSK调制下的误码率却有明显差别, 原始信号的误码率曲线在最上方, LS-ACE-POCS算法的误码率曲线稍微浮于ACE-POCS算法的误码率曲线。同样由Matlab仿真可知, 在SNR=12 dB处, 原始信号、 ACE-POCS算法调制、 LS-ACE-POCS算法调制的BER分别是3.516×10-5、3.027×10-5、2.832×10-5(dB)。

图6 3种算法的BER性能对比图Fig.6 BER performance comparison diagram of three algorithms
3.3 结 论
由上述仿真结果可知, 在相同的模拟条件下, 采用算法的误码率性能比不采用算法的误码率性能要好, 采用LS-ACE-POCS算法的误码率性能比采用ACE-POCS算法的误码率性能稍好一些, 但比原始信号的误码率要好许多, 因此LS-ACE-POCS算法的误码率性能是可以接受的。
4 LS-ACE-POCS算法的时间复杂度分析

采用ACE-POCS算法时, 每次迭代都只在调制处有1次FFT/IFFT运算, 即时间复杂度是10*O(NLlog2NL)。采用LS-ACE-POCS算法时, 由于e是所有|y(n)|>0的集合, 设e中有T个元素, 因此实施的实数加法计算量是2T-1, 实数乘法的计算量是2T+1, 最终的时间复杂度是O(2T+1)。LS-ACE-POCS算法是ACE-POCS算法与最小二乘估计法[21]的融合, 即该算法的时间复杂度为O(NLlog2NL)+O(2T+1)。比较这两个算法的计算复杂度大小, 由于T≤N,NLlog2NL≥2T+1, 因此LS-ACE-POCS算法的计算复杂度比ACE-POCS算法的计算复杂度小很多, 系统的复杂度性能大大优化了。
5 结 语
为解决峰均功率比过高引起的一系列问题, 笔者提出LS-ACE-POCS算法, 即采用最小二乘估计找到一个最优因子, 与消峰信号相乘, 使产生的新的消峰信号与原始噪声最大程度的接近, 大大减少了迭代次数, 提高了系统的收敛速度, 使1次的迭代效果能与原先10次的迭代效果相媲美。在降低PAPR性能上限幅阈值A=1.923为最佳, 采用QPSK调制为最佳, 合理范围内子载波数目越多越好。关于误码率, QPSK调制比16QAM调制的误码率性能优异, 在QPSK调制下, 采用算法比不采用算法的误码率性能好, 采用LS-ACE-POCS算法比采用ACE-POCS算法的误码率性能要优异。在降低系统的时间复杂度方面, 采用LS-ACE-POCS算法产生的时间复杂度远远小于ACE-POCS算法。综上得出, LS-ACE-POCS算法要比ACE-POCS算法优异, 因此该算法是个可取方案, 有很强的实用性。

