限幅特性在鱼雷控制系统设计中的应用

王改娣, 黄华红, 吕艳慧



限幅特性在鱼雷控制系统设计中的应用

王改娣, 黄华红, 吕艳慧

(中国船舶重工集团公司第705研究所, 陕西西安, 710075)

限幅特性技术在鱼雷控制系统设计和工程实现中已被广泛应用, 本文以继电控制的鱼雷深度纵倾系统为例, 分析了限幅器的限幅特性作用机理和系统工作原理, 在对系统数学描述的基础上, 进行了限幅参数优化仿真计算与分析。结果表明, 限幅特性不但可以方便地实现控制状态的自动转换, 而且可以发挥系统最大能力, 使得鱼雷寻深弹道到达最优, 满足鱼雷深浅水的使用要求, 该结论对工程设计具有指导意义。

鱼雷控制系统; 限幅特性; 参数优化; 寻深弹道; 仿真

0 引言

对鱼雷控制系统来说, 无论是线性控制系统还是非线性控制系统, 在设计和应用中, 通常存在或人为加入了多种限幅器。现以鱼雷深度纵倾通道为例来分析这些限幅器及其限幅特性在鱼雷控制系统中的应用。

图１为鱼雷控制系统限幅设计示意图。从图中可以看出, 鱼雷深度纵倾控制系统是一个具有非线性环节的复杂控制系统, 其被控对象为雷体, 被控量为鱼雷深度。由内到外包含了3个闭环控制环路, 即角速率控制环路、角度控制环路和深度控制环路, 每个环路都存在有限幅器, 不同限幅器发挥着不同的作用。

本文将图1中限幅器的限幅特性分为两类, 一类是控制器件本身存在的限幅特性, 如限幅器3~限幅器6; 另一类是控制系统设计时人为加入的限幅特性, 如限幅器1和限幅器2。第1类限幅特性是根据鱼雷研制中总体要求和控制器件实现的可行性所确定的, 在实际产品中客观存在。由于第1类限幅器涉及到产品组件设计和加工的可行性等问题, 本文不过多赘述。本文着重分析和回答第2类限幅器的应用。

为了方便说明, 以继电控制的鱼雷深度纵倾系统为例来讨论这类限幅器作用、限幅特性的设计以及系统工作原理, 并通过仿真说明如何与控制系统参数进行综合设计优化, 使得控制系统性能达到最优。

1 系统数学描述

假设图1中控制律为继电方式, 舵机小回路为速率控制方式, 则该系统简化后的数学描述如图2所示。图中,为舵机传递函数;为雷体传递函数;为水平舵角, rad;为俯仰角速率, rad/s;为俯仰角, rad;表示深度, m;为速度, m/s;表示设定深度, m;为俯仰角速率控制系数;为深度微分控制系数;为深度控制系数;~为相应限幅器的限幅值。

图2 深度控制的数学模型框图

图2中为了减小入水初始段姿态传感器输出误差对深度控制精度的影响, 而直接引入深度微分信号参与控制。根据系统工作原理和模型特点, 决定了本文讨论的鱼雷控制系统是利用固有振荡的振荡伺服系统, 其振荡特性与控制参数设计有关, 本文只研究控制系统中的限幅特性对初始寻深弹道的影响。

2 限幅特性作用机理

根据图2, 在鱼雷入水后寻深定深过程中, 由于运动参数的大范围变化, 鱼雷深度纵倾通道往往会出现3种控制状态, 即角速率控制、定角爬潜控制和定深控制, 鱼雷瞬态只能处在一种状态中, 这3种状态会自动转换。

如前可知, 鱼雷深度纵倾控制系统由内到外包含了角速率控制、角度控制和深度控制3个闭环控制环路。当鱼雷入水时, 设定的搜索深度与鱼雷初始深度的瞬时深度差使限幅器1呈限幅状态, 若限幅器2未限幅, 鱼雷则以限幅器1的限幅值为指令, 实现定深度速率或定角爬潜运动。如果在这一过程中, 限幅器2出现了限幅, 鱼雷则以限幅器2的限幅值为指令, 实现定角速率控制下的旋回运动。随着鱼雷深度的增大, 与搜索深度差值减小, 限幅器1进入线性状态, 系统处于深度控制状态。

根据系统的工作原理, 限幅特性在控制状态转换中的作用机理如下。

1) 当限幅器2工作在限幅状态时, 系统呈现角速率控制状态, 即角速率环路在工作, 限幅值成为角速率指令, 综合控制电压为

2) 当限幅器1工作在限幅状态时, 而限幅器2不限幅时, 系统呈现深度速率或定角控制状态, 即深度速率或姿态环在工作, 限幅值成为深度速率或姿态指令, 综合控制电压为

(2)

3) 当限幅器1和限幅器2均未工作在限幅状态时, 系统呈现深度控制状态, 即深度环在工作, 此时的综合控制电压为

需要强调的是, 以上控制状态转换是自动进行的，完全取决于鱼雷所处的瞬态运动, 并不是按照弹道设计顺序或程序控制进行的固定转换。

3 限幅参数优化及仿真分析

优化设计限幅值, 可使系统处于最优控制状态, 鱼雷一入水, 就以可用的最大机动能力快速稳定地进入定深状态。下面将针对限幅器2和限幅器1的作用来开展仿真研究。

3.1 限幅器2

限幅器2直接影响到内回路稳定性, 所以首先应该确定限幅器2的限幅值。从图2不难看出, 限幅器2是对角速度指令的限幅, 它限制了角速度指令的最大施加值, 由速率控制方式可知, 它的设计应符合

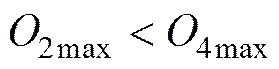
不难看出, 限幅值的选取应小于速率传感器的限幅值, 如果不满足式(4), 则会引起控制系统失稳发散。所以, 对于本文所研究的系统, 要求限幅值在不影响系统振荡参数的前提下, 又要发挥出敏感元器件的最大能力。

在其他控制参数不变的情况下, 假设舵机限幅为10°, 速率传感器的输出限幅为40°/s, 设定限幅值分别为35°/s和45°/s, 则得到鱼雷的实际角速率ω和舵角δ的仿真结果曲线如图3所示。

图3 不同限幅值对输出影响

在分析图3仿真结果时, 要考虑伺服振荡控制系统的输出特性, 即角速率按照一定周期和幅值振荡变化。从图3(a)可看出, 若限幅值小于速率传感器本身的限幅值, 则系统靠振荡实现稳定控制, 图3(b)中一旦限幅值大于, 系统将停止振荡, 舵角限幅, 角速度增大, 实际系统将失控发散。

进一步的研究表明,限幅值的选取, 还可以根据需要在弹道不同阶段选取不同的数值, 以限制鱼雷在纵平面运动的俯仰角速度, 如鱼雷上限控制时, 为了避免鱼雷上爬跳水、动力系统燃料晃动等, 可适当减小限幅值。

3.2 限幅器1

对于定深控制, 限幅器1的限幅值选择, 是在其他控制参数及限幅值确定的条件下进行的, 其目的是使鱼雷大俯仰角入水时, 初始袋深最小, 而在小俯仰角入水时, 深度不出现反弹现象, 尤其是对鱼雷的浅水控制, 限幅值的选择很重要。

根据图1和图2工作原理, 鱼雷入水初期, 存在大深度差时, 限幅值不但决定了环路2与环路3的转换深度, 而且还控制了鱼雷爬潜角度, 爬潜角度计算公式

式(5)中的值, 应根据不同的弹道要求确定, 对于深水寻深弹道, 应满足定角下潜要求, 对于浅水寻深弹道, 应满足浅水弹道最优控制效果。

在3.1节研究的基础上, 设定y为-35 m, 初始深度为-5 m, , 通过改变限幅值, 对鱼雷在不同入水角(分别为-10°,-88°)下的寻深弹道进行仿真计算, 得到鱼雷深度超调△及达到最大深度时间的仿真结果(见表1), 同时为了对比分析入水角对寻深弹道的影响, 图4给出了为10 m时不同入水角下运动参数仿真曲线。

从表1的仿真结果可以看出, 对于小姿态角入水条件, 限幅值决定了鱼雷在寻深过程中下潜角的大小,越大, 下潜角越大, 寻深时间越短, 但深度超调也越大。对于大姿态角入水条件, 鱼雷首先以系统的最大机动能力即限幅值进行角速度控制下深度拉平, 限幅值在一定范围内不影响控制效果, 但随着继续增大, 寻深时间变长且深度超调增大。

根据图4, 在同一限幅值下, 由于入水参数的不同, 下潜过程的控制方式也不同, 说明了本文研究的限幅特性和是可自动实现控制状态转换的。

表1 不同入水角下深度超调仿真结果

图4 O1=10 m时不同入水角下运动参数变化曲线

若限幅参数选取得当, 即可保证寻深弹道不会出现过大超调, 又可快速平稳过渡到搜索深度上。不难看出, 对本文所研究的系统及设定的仿真条件, 限幅值在10 m左右时, 深度超调和到达最大深度的时间比较匹配, 可为最优选择。

4 结束语

本文针对具有继电控制的鱼雷控制系统, 研究了限幅器的类型和作用, 在对系统进行数学描述的基础上, 首先对不同限幅器的限幅特性作用机理和系统工作原理进行了分析, 然后进行了限幅参数的优化和对系统影响的仿真计算。研究结果表明, 限幅特性可方便地实现对弹道参数和弹道不同阶段的运动参数的限制, 可自动实现控制状态和控制方式的转换, 限幅特性与控制参数综合选择可以使鱼雷初始弹道达到最优, 其效果是仅依靠控制系数优化所不能达到的。

[1] 徐德民.鱼雷自动控制系统[M]. 西安: 西北工业大学出版社, 1991.

[2] 高剑, 徐德民, 潘瑛, 等.鱼雷纵向运动的非线性自适应滑模控制[J]. 弹箭与制导学报, 2005, 25(3): 155-157. Gao Jian, Xu De-min, Pan Ying, et al. Nonlinear Ad- aptive Sliding-Mode Controller for the Longitudinal Control of the Torpedo[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2005, 25(3):155-157.

[3] 绪方胜彦(美). 现代控制工程[M]. 4版. 卢伯英, 于海勋, 译. 北京: 电子工业出版社, 2003.

[4] 张宇文. 鱼雷弹道与弹道设计[M]. 西安: 西北工业大学出版社, 1999.

(责任编辑: 杨力军)

Application of Amplitude Limit Characteristic to Torpedo Control System Design

WANG Gai-di, HUANG Hua-hong, LÜYan-hui

(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China)

The action mechanism of amplitude limit characteristic and system working principle are analyzed by taking an example of a torpedo depth pitch system with relay control. Based on the mathematical description of this system, the amplitude limit parameters are optimized and analyzed via simulation. The results show that the amplitude limit characteristic can realize the automatic transition of control status, maximize system capacity, and optimize the depth searching trajectory for torpedo to meet the requirement of torpedo usage in deep or shallow sea.

torpedo control system；amplitude limit characteristic; parameter optimization; depth searching trajectory; simulation

TJ630.33

A

1673-1948(2011)06-0451-04

2011-03-03;

2011-05-03.

王改娣(1964-), 女, 研究员, 主要从事鱼雷总体性能和弹道仿真建模研究.