一种多测点变工况倍频程快速处理方法

孙 涛, 高爱军, 王 祎, 都治国



一种多测点变工况倍频程快速处理方法

孙 涛, 高爱军, 王 祎, 都治国

(中国船舶重工集团公司第705研究所, 陕西西安, 710075)

针对传统倍频程分析方法处理多测点变工况振动噪声数据耗时费力的不足, 提出一种改进的适用于多测点变工况振动噪声数据快速处理的倍频程方法。首先对整个试验过程所有测点的数据进行分块倍频程处理, 然后利用工况参数确定稳定工况, 根据稳定工况的起止时间计算对应的性能参数均值及连续频段振级均值, 最后, 以判定工况的性能参数为索引将各测点相同工况的性能参数均值及连续频段振级均值比邻放置, 得到满足统计要求的3D统计矩阵。工程应用表明, 采用改进算法不但大大提高了试验数据的分析效率, 而且相对传统算法明显提高了分析深度。

倍频程分析方法; 振动噪声; 数据处理; 倍频程谱

0 引言

倍频程谱是根据人耳对声音的响应特性构造的一种频域分析方法, 具有谱线少频带宽的特点, 广泛应用于声学信号的分析处理。声音来源于振动, 二者之间有很好的相关性, 因此倍频程谱也常用于环境振动的测量分析与评估。此外, 针对在工业现场难以直接使用噪声测量仪器来测试机器的噪声, 一些学者开展了“以振代声”的研究, 将倍频程谱引入到机电设备的监测诊断领域, 取得较好的应用效果。目前倍频程处理已成为各类商用振动噪声分析软件必不可少的功能。

大型变工况振动噪声试验(比如船用发动机、飞机发动机、鱼雷动力装置的振动噪声试验)通常需要连续采集几十甚至几百个测点的多工况数据, 对每个测点的数据按照工况进行倍频程处理是评估被测对象振动噪声水平的最常用手段之一。目前的商用振动噪声分析软件只具备单测点单工况/多测点单工况倍频程处理功能, 用其处理多测点变工况振动噪声数据十分费时耗力: 从计算角度而言, 每计算一种工况条件下的倍频程谱就必须修改一次参数设置, 对整个试验过程数据的处理就需要多次中断计算过程修改参数设置; 从结果输出而言, 每次只能将一种工况对应的倍频程计算结果输出到文件中, 要得到满足统计要求(根据试验流程将相同工况对应的振级序列排列在一起)的振级序列排列结果需靠手工调整不同文件中的数据, 非常繁琐且易出错。

为了弥补传统的倍频程分析方法在实际工程应用中的不足, 本文提出了一种多测点变工况振动噪声试验数据的倍频程快速处理方法, 通过将性能参数和振动参数有效融合, 实现了输入和输出均一次完成, 大大减少了数据处理时间, 降低了工作强度, 并可挖掘出更多的有用信息。

1 单测点单工况倍频程谱算法

倍频程谱实际上是频域分析中频率的一种相对尺度, 由一系列频率点以及对应这些频率点附近频带内信号的有效值所构成。单测点单工况倍频程谱算法如下。

(2)

(3)

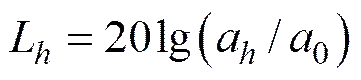
计算不同频段振级可得到以中心频率为横坐标, 中心频率对应级值为纵坐标的倍频程谱。

2 多测点变工况倍频程快速处理算法

机电设备变工况振动噪声测试过程中, 除了测量不同位置和方向的振动噪声, 还测量变工况运行过程中的性能参数(含工况参数), 二者是紧密联系在一起的。传统的倍频程分析技术无法将这两种信息有效融合, 因而无法实现变工况倍频程的批处理和统计处理, 并且处理结果不含任何性能信息。为了将振动参数和性能参数进行有效融合, 构造了如图1所示的多测点变工况振动噪声数据倍频程分析流程, 具体算法如下。

1) 将整个试验过程的振动数据按测点分块进行倍频程处理, 得到由不同的频段振级块组成的连续频段振级矩阵和块号时间矩阵。

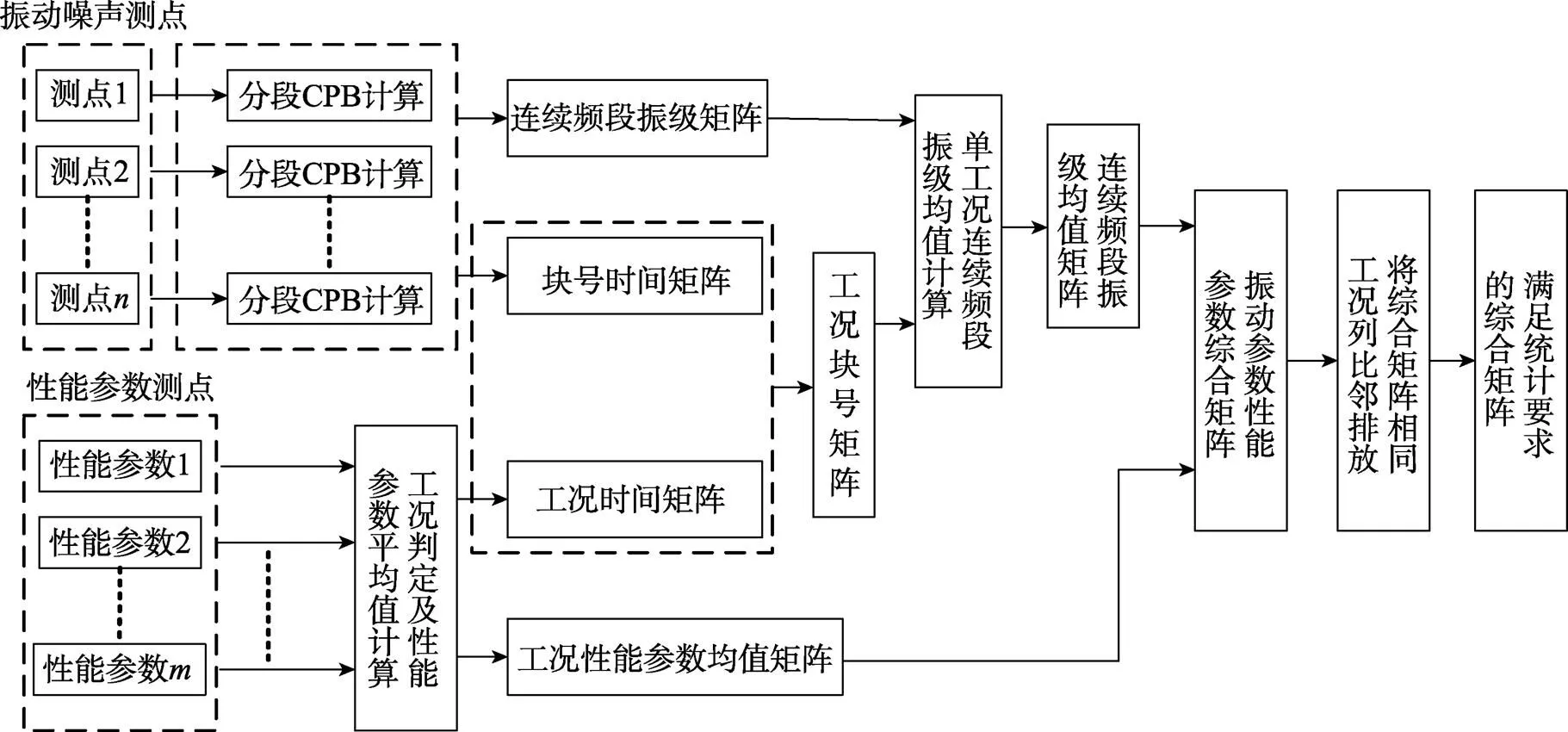
图1 多测点变工况振动噪声数据倍频程分析流程

2) 根据与振动参数同步测量的性能参数来确定稳定工况对应时间段(判定稳定工况的性能参数及条件视试验而定), 进而计算性能参数均值, 建立工况时间矩阵和工况性能参数均值矩阵。

性能参数测试数据对应的时刻由性能数据的采样率决定, 设采样率为, 稳定工况对应的性能数据序号为, 则稳定工况对应时间段为。

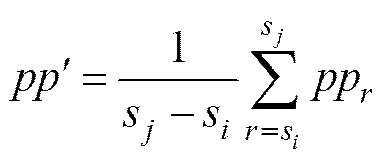
3) 由稳定工况对应的时间段确定其所对应的起止频段振级块号。

4) 计算任意测点任意工况的连续频段振级均值, 任意频段的振级均值计算方式如下。

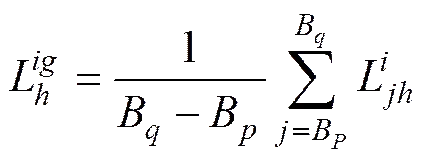
5) 按照工况发生先后顺序计算所有测点所有工况的连续频段振级均值。

6) 按照测点编号将不同测点所有工况的连续频段振级均值存入与之对应的矩阵。

7) 依次将性能参数均值矩阵和各测点的连续频段振级均值矩阵合并形成各测点的综合矩阵。

8) 以判定工况是否相同的性能参数为索引按照相同工况比邻放置的原则调整各测点综合矩阵的列, 得到满足统计要求的统计矩阵。

9) 依次将各测点的统计矩阵输出到Excel文件的各张电子表。

3 工程应用

航速航深是鱼雷动力装置重要的技术指标。为了对动力装置的工作性能进行有效考核, 功率试验过程中需多次变换工况(变换速制和深度), 并测量反映动力装置振动特性和工作性能的几十种振动和性能数据(包括转速、转矩、功率、背压、流量及众多位置的振动信号)。稳定工况指在速制不变的情况下, 流量调节器背压的测量值与该时间段内平均值的相对偏差不超过允许范围。下面以某次功率试验的测试数据为例来说明倍频程快速处理方法的工程应用及其优越性。

试验流程包括由速制(试验规定在一定范围的转速为同一速制)和背压组合而成的若干工况。动力装置上布置了20个振动测点及若干性能参数测点, 性能参数为缓变信号, 采用慢采, 振动信号为中高频信号, 采用快采。稳定工况涉及速制和背压2个参数, 因此调整各测点的综合矩阵时, 首先将相同速制的各列数据放在一起, 然后按照背压的升序对相同速制的数据按升序排列, 得到满足统计要求的统计矩阵。

数据处理结果得到各个测点的统计矩阵。统计矩阵的第1行为工况对应的起始时间, 第2行为工况对应的终止时间, 第3行到第7行分别对应速制、压力、流量、转速和功率的均值, 其余行分别对应1/3倍频程的各频段振级。基于MALTAB的程序可将统计矩阵输出到Excel文件, 这样就将振动信息、性能信息和工况的对应关系在一张表中显示, 既便于使用者浏览又便于对振动和工作性能之间的关系做进一步的分析。与采用传统的倍频程分析方法相比, 数据处理效率提高了约20倍。

本方法不但处理多测点变工况振动噪声数据倍频程谱的效率高于传统方法, 而且能提供更多的有用信息。本次试验某测点在4个相同工况下的平均振级谱见图2。实线和点线对应磨合前的2个工况, 虚点线和虚线对应磨合后的2个工况。可以看出, 在相对中心频率21.5以上(含21.5)的频率范围, 磨合后各频段的振级低于磨合前相同频段的振级。采用商业软件处理这种多测点变工况数据时, 为了节约处理时间, 通常只从相同工况中挑一组数据来处理, 则无法得出磨合前后振动差异的规律, 更无法为样机确定合理的磨合时间。该测点的综合矩阵输出到Excel文件“试验数据处理”的第一张电子表sheet1, 利用Excel的绘图功能绘出的某速制某频段振级压力变化的折线图见图3。可以看出, 当压力持续增加到某临界值(压力序号11对应的值)之上, 振级的增加出现突变。如果不将振动信息和性能信息结合, 则无法得出振动随压力的变化规律。

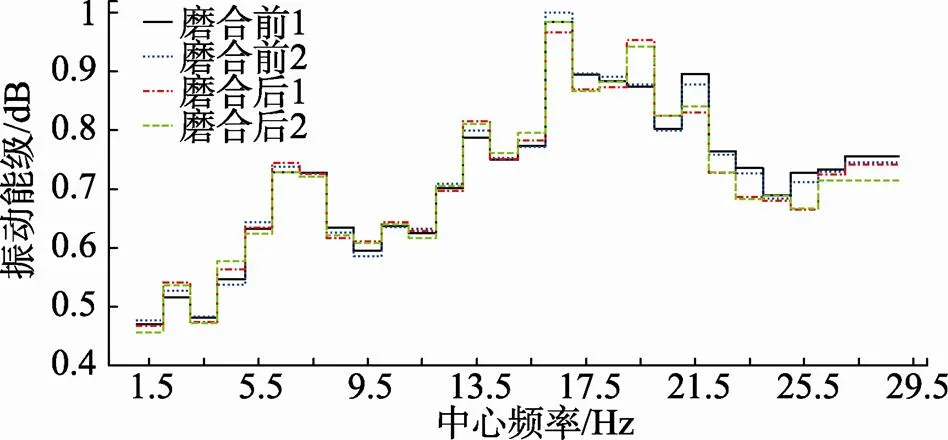
图2 分析测点在4个相同工况下的平均振级谱

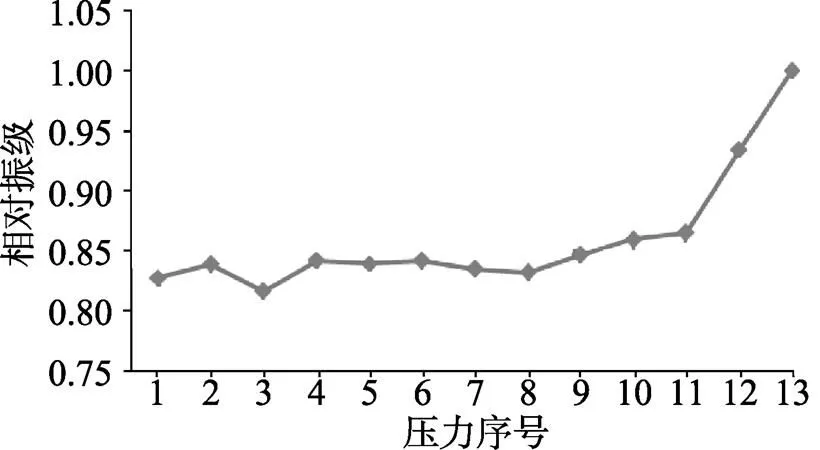
图3 分析测点某频段振级随压力变化的规律

4 结束语

随着科学技术的飞速发展, 机电设备朝着大型化、复杂化、自动化和一体化方向发展, 对振动噪声测量分析提出了更高的要求。多测点变工况振动噪声测试已成为工程振动噪声测试的发展方向, 然而目前的商用振动噪声分析软件处理多测点变工况振动噪声数据的倍频程谱相当费时耗力。为此, 本文提出一种多测点变工况倍频程快速处理方法。该方法在鱼雷动力装置功率试验振动数据处理的应用表明, 其“傻瓜式”操作大大降低了多测点变工况性能参数和振动参数的处理时间和工作强度, 基本实现了试验结束即可给出不同工况不同测点不同频段的振动大小及热力参数统计值, 据此可现场评判振动是否达标, 并确定超标频段。本方法是对倍频程方法的改进, 在倍频程方法的应用领域具有一定的推广价值。

[1] 庞剑, 谌刚, 何华. 汽车噪声与振动—理论与应用[M]. 北京: 北京理工大学出版社, 2006.

[2] 申跃奎,丁洁民, 陆秀丽. 地铁激励下房屋的环境振动与隔振设计[J]. 建筑结构, 2010, 40(10): 78-81.

Shen Yue-kui, Ding Jie-min, Lu Xiu-li. Environment Vibration Induced by Subway and Vibration Isolation of a building[J].Building Structure, 2010, 40(10): 78-81.

[3] 王文斌, 刘维宁, 马蒙, 等. 梯形轨道系统动力特性及减振效果试验研究[J]. 中国铁道科学, 2010, 31(2): 24-28.

Wang Wei-bin, Liu Wei-ning, Ma Meng, et al. Expe- rimental Study on the Dynamic Characteristics and the Vibration Mitigation Effect of Ladder Track System[J]. China Railway Science, 2010, 31(2): 24-28.

[4] 葛勇, 张希黔, 严春风, 等. 无砟轨动车组运行激励场地振动谱分析[J]. 地震工程与工程振动, 2010, 30(1): 15-21.

Ge Yong, Zhang Xi-qin, Yan Chun-feng, et al. A Test of the Ground Vibrations Induced by Ballastless Truck Running[J]. Journal of Earthquake Engineering and En- gineering Vibration, 2010, 30(1): 15-21.

[5] 李联玉, 马孝江, 蔡庆喜. “以振代噪”在汽车变速箱性能检测中的应用研究[J]. 机床与液压, 2004(7): 156- 157.

Li Lian-yu, Ma Xiao-jiang, Cai Qin-xi. Application and Research of “Substituting Vibration for Sound” App- roach in Test for Performance of Motorcar-Gearbox [J]. Machine Tool & Hydraulics, 2004(7): 156-157.

[6] 袁云龙, 袁超勇, 杨超珍. 频段能量统计法在机械设备工作状态监测中的应用[J]. 轻工机械, 2010, 28(2): 85-88.

Yuan Yun-long, Yuan Chao-yong, Yang Chao-zhen. App- lication of Frequency Band Energy Statistics Method to Monitoring the Work Conditions of Mechanical Equip­ment[J]. Light Industry Machinery, 2010, 28(2): 85-88.

[7] 王济, 胡晓. MATLAB在振动信号处理中的应用[M]. 北京: 中国水利水电出版社, 2006.

(责任编辑: 陈 曦)

A Fast CPB Processing Method of Off-design Vibration and Noise Data from Multiple Channels

SUN Tao, GAO Ai-jun, WANG Yi, DU Zhi-guo

(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China)

To solve the time-consuming and laborious problem in processing the off-design vibration and noise data from multiple channels through the traditional constant proportional bandwidth (CPB) method, an improved CPB method is proposed. Firstly, the data from all channels are divided into multi-segment, and each segment is calculated via octave algorithm based on fast Fourier transform (FFT) algorithm. Secondly, technical parameter mean and average octave sequence are calculated according to the starting and ending time corresponding to the stable condition determined by the condition parameter curve. Finally, technical parameter mean and average octave sequence of the same working condition are adjusted to the adjacent columns by indexing the condition-determining parameters. Engineering application shows that the analysis efficiency and depth of test data are improved significantly.

constant proportional bandwidth (CPB) method; vibration and noise; data processing; octave spectrum

TJ630; TB52

A

1673-1948(2011)06-0455-04

2011-01-24;

2011-05-12.

孙 涛(1977-), 男, 博士, 高级工程师, 研究方向为机械信号处理、制造工艺过程振动控制、故障诊断及健康监测.