舰载武器SINS非线性传递对准模型及滤波算法

李 娜, 王新龙



舰载武器SINS非线性传递对准模型及滤波算法

李 娜, 王新龙

(北京航空航天大学宇航学院, 北京, 100191)

为了满足舰载武器初始对准高精度和快速性的要求, 更好地解决舰载武器在大失准角情况下的传递对准问题, 提出了一种结合基于四元数的非线性传递对准模型与非线性无迹卡尔曼滤波(UKF)算法的方法, 推导并建立了舰载武器捷联惯导系统(SINS)的非线性误差模型。该模型采用姿态四元数表示姿态误差, 以提高姿态解算时的快速性和精度, 选用速度加姿态作为量测量, 以提高系统的可观测性, 采用奇异值分解(SVD)方法解决了方差阵的病态问题, 以确保算法的鲁棒性, 仿真结果表明, 该方法不仅解决了舰载武器在大失准角情况下的传递对准问题, 而且能够有效提高传递对准的精度和快速性, 其计算精度和对准时间满足系统设计要求。

舰载武器; 捷联惯导系统; 非线性; 四元数; 无迹卡尔曼滤波; 传递对准

0 引言

为了提高舰载武器的快速反应能力, 对捷联惯导系统(strap-down inertial navigation system, SINS)对准的快速性和精确性提出了越来越高的要求。传递对准是解决SINS动基座对准问题的主要方法。它是通过引入高精度的主惯导信息, 以此为基准运用卡尔曼滤波器来估计子惯导系统的速度误差、姿态误差和惯性器件误差等状态变量的值, 从而对子惯导信息进行补偿。

由于舰载武器的多样化以及低成本、小型化惯性器件的飞速发展, 在舰载武器传递对准过程中, 子惯导系统惯性器件的精度较低, 这会导致惯导计算产生较大的误差, 并且主、子惯导之间的安装误差、杆臂效应、弹性变形等因素的影响也会产生较大的姿态误差, 从而影响传递对准的精度。

捷联惯导系统的精对准一般需在完成粗对准的基础上进行, 通过舰载武器SINS陀螺仪和加速度计的输出值, 与对准点已知的重力加速度和地球自转角速度的矢量值构造方程, 计算出载体的姿态矩阵, 从而完成粗对准。而舰船在摇摆状态下, 摇摆引起的干扰角速度远大于地球自转角速度, 陀螺输出的信噪比很低, 且干扰角速度具有很宽的频带, 无法从陀螺输出中提取地球自转角速度, 粗对准实现起来很困难, 因此工程上往往希望可以在初始失准角较大的情况下直接进行精对准。此时如果仍然使用适用于小角度传递对准的线性模型进行估计, 将会导致很大的对准误差。姿态四元数作为描述刚体旋转运动的方法之一, 在许多领域得到了广泛应用。与传统的欧拉方法相比, 四元数对姿态转动的描述更简洁, 且四元数方程是线性微分方程, 具有线性化程度高、求解速度快、精度高及方程无奇异等优点。

无迹卡尔曼滤波(unscented Kalman filter, UKF)是Juliter等人提出的基于UT (unscented transformation)的卡尔曼滤波方法, 它是利用选取好的一组确定的采样点对状态变量的概率密度函数进行线性化, 然后再利用卡尔曼滤波的框架进行递推滤波。UKF方法不需要计算雅可比矩阵, 不需要对状态方程和量测方程线性化, 因此也就不像广义卡尔曼滤波（extended Kalman filter, EKF）线性化处理时存在较大的截断误差。为了保证UKF算法的鲁棒性, 采用奇异值分解的方法解决滤波过程中的方差阵的病态问题。

本文推导并建立了一种适用于舰载武器的基于四元数的非线性传递对准模型, 并采用速度加姿态的匹配方式与改进的UKF滤波算法相结合, 以提高舰载武器初始对准的精度和快速性。

1 非线性传递对准模型的建立

1.1 系统状态方程的建立

1.1.1 杆臂效应误差补偿

杆臂效应是由于惯性测量组件安装位置与载体中心不重合而引起加速度输出中的干扰加速度, 它相当于加速度计的附加测量误差。设安装在载体上的惯性测量组件其加速度计偏离摇摆中心的距离(杆臂长度)为, 则由杆臂效应引起的干扰加速度为

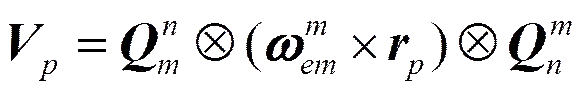
对式(2)求导, 并将式(1)代入, 得到杆臂效应速度微分方程

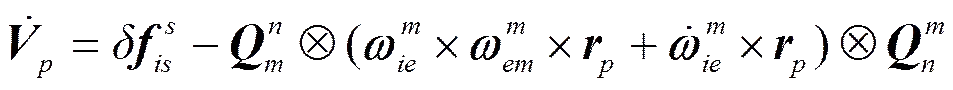
1.1.2 速度误差方程

由于安装误差及陀螺漂移等各种因素的影响, SINS数学平台系与导航坐标系之间存在平台失准角矢量,而导航系相对数学平台系的姿态四元数可表示为

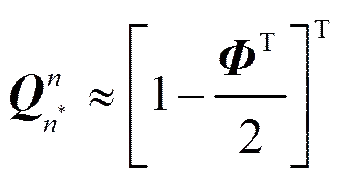
(5)

主惯导系统的速度误差微分方程表示为

子惯导系统的速度误差微分方程表示为

(7)

若子惯导的速度误差定义为

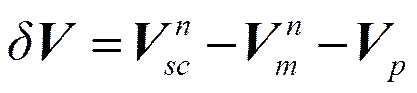
对上式两端求导, 并将式(3)、式(5)~式(7)代入得

(9)

1.1.3 姿态误差方程

假设主惯导系统的惯性元器件不存在误差, 则主惯导系统的姿态四元数微分方程表示为

(11)

子惯导系统的姿态四元数微分方程为

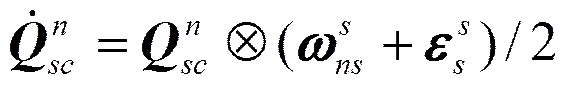
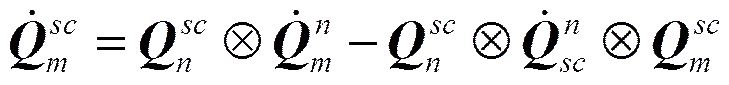
(14)

基于姿态四元数的快速传递对准模型的状态方程形式表示为

假设子惯导系统的陀螺漂移和加速度计偏差为常值、主子惯导的相对位置固定不变, 并且认为, 则可以得到系统的状态方程表达式

1.2 系统量测方程的建立

由于“速度+姿态角”匹配能同时兼顾计算参数和测量参数2种匹配方式的优点, 因此这里采用“速度+姿态角”匹配方式, 以主、子INS的速度和姿态角输出差值作为量测量。那么, 基于四元数的传递对准模型量测方程为

(18)

2 三轴摇摆运动模型及可观测性分析

捷联惯性系统在三轴摇摆运动时的条件为载体以正弦规律绕航向轴、纵摇轴和横摇轴摇摆, 其数学模型为

(20)

(21)

在设计卡尔曼滤波器之前, 通常先进行系统的可观测性分析, 以确定滤波器的估计效果。由于舰载武器捷联惯导是一个时变系统, 所以其可观测性分析比定常系统复杂的多。如果用分段线性定常系统 (piece-wise constant system, PWCS)代替时变系统, 利用Meskin和Itzhack的可观测矩阵(stripped observable matrix, SOM)代替总的可观测阵(total observability matrix, TOM)来分析, 可使分析过程大为简化。虽然这种分段定常系统可观测性分析方法可定性地分析系统的可观测性, 但无法定量地描述各状态变量的可观测程度。因此本文采用了一种能够定量分析系统状态可观测度的奇异值分解方法。这种方法不需要事先进行滤波运算, 就可直接简单地实现系统的可观测度分析。它根据每个状态所对应的奇异值的大小, 即可判断状态变量的可观测度。较大的奇异值对应的状态变量可以获得较好的估计。反之, 当奇异值非常小或为零时, 状态变量不可观测。

根据舰船摇摆运动特点, 采用“速度+二轴摇摆”和“速度+三轴摇摆”运动模型在60 s的时间段内进行可观测度分析。对于舰载武器非线性传递对准模型(16)和(18), 首先将非线性系统模型线性化得到系统的可观测阵, 然后利用分析线性系统的奇异值分析方法得到各状态变量的可观测度, 如图1所示(这里取舰船绕航向轴、纵摇轴和横摇轴的摇摆角度幅值,,摇摆周期分别为,,初始航向为初始相位都为零, 舰船速度为)。

分析表明, “速度+二轴摇摆”时不考虑方位轴的艏摇, 可观测矩阵的秩为13, 其中三轴速度误差、主惯导载体坐标系和子惯导解算的载体坐标系之间的姿态误差四元数、主惯导载体坐标系和子惯导真实载体坐标系之间四元数、东向和北向陀螺漂移以及2个轴向的杆臂长度, 这13个状态变量的可观测度较好, 其余状态变量的奇异值很小,可认为状态不可观测; 而“速度+三轴摇摆”运动增加了方位轴向的角速度运动, 与“速度+二轴摇摆”运动相比, “速度+三轴摇摆”运动在可观测度增加的同时, 不可观测量也变得可观测。因此, 本文选了“速度+三轴摇摆”运动模型, 这时卡尔曼滤波器可对系统状态进行很好的估计, 从而使舰载武器SINS对准时可以获得更好的对准性能。

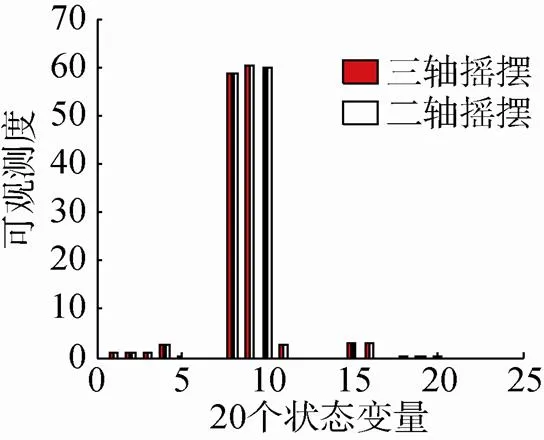
图1 状态变量可观测度分析结果

3 UKF算法特点与分析

EKF是一种应用广泛的非线性系统滤波方法, 应用时首先需要将系统非线性模型进行泰勒展开, 保留1阶项而忽略高阶项以实现模型的线性化处理, 因此线性化处理后的系统模型存在较大的截断误差, 从而影响了模型的精确性, 降低了滤波的精度。而且, EKF将状态方程中的模型误差作为过程噪声来处理, 且假设该噪声为高斯白噪声, 这与实际舰载武器SINS的实际噪声情况并不相符。

近年来出现了一种基于UT变换的UKF非线性滤波算法。UKF算法的核心思想是: 首先, 在原状态分布中取一些点, 使这些点的均值和协方差等于原状态分布的均值和协方差; 再将这些点代入非线性函数中, 得到非线性函数值点集, 通过该点集求取变换后的均值和协方差; 最后, 根据正交投影法则导出递推公式。对于线性系统来说, 它的滤波性能与卡尔曼滤波相当, 但对于非线性系统, 它的性能则明显优于EKF滤波算法。

对于如下一个连续非线性系统

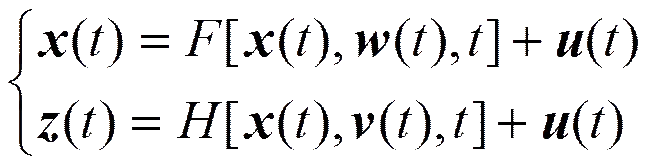
UKF算法的主要步骤概括为以下方面。

1）首先, 采用4阶Runge Kutta法以数值积分的方法将系统模型进行离散化, 得到一个离散非线性系统

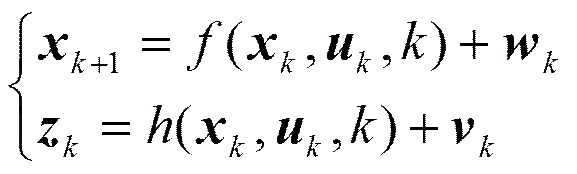
2）进行初始化

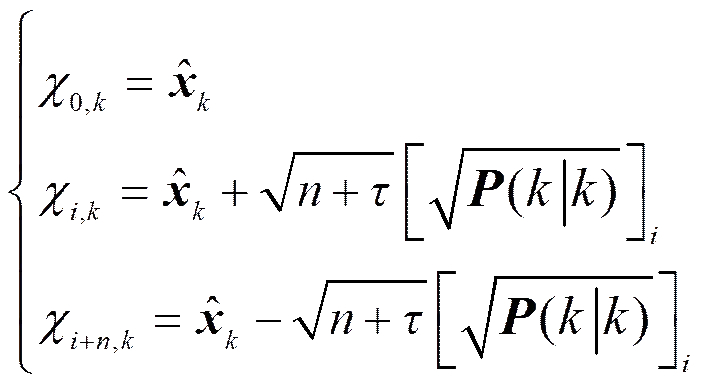
计算采样点的权重

(26)

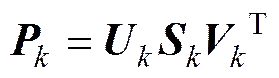
5) 时间更新

状态向量的一步预测值为

(29)

一步预测均方误差为

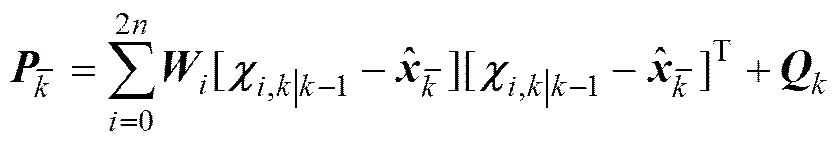
量测值的一步预测为

(31)

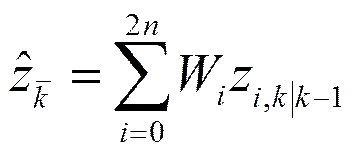
6) 量测更新

量测值的估计均方差方程

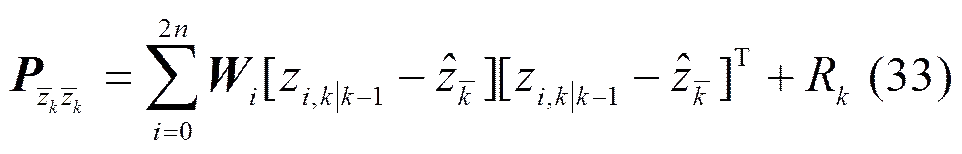
滤波器增益方程

状态变量估计值的更新

(36)

状态变量估计均方误差方程

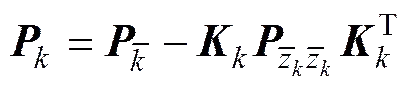
从上述UKF算法的主要步骤可看出, 这种UKF算法不再局限于系统或量测噪声为高斯分布的情形, 不需要计算雅可比矩阵, 也不需要对状态方程和量测方程进行线性化处理, 因此, 也就不像EKF线性化处理时存在较大的截断误差。

4 仿真结果与分析

舰船三轴摇摆运动模型参数同第2节进行系统可观测性分析时是一致的。其他参数设置如下。

7) 估计误差均方差初值为

8) 系统噪声方差阵为

量测噪声方差阵为

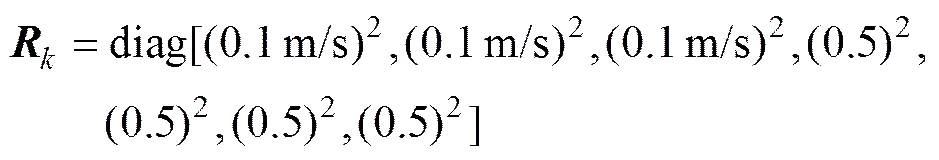
选取地理坐标系为导航坐标系, 载体坐标系为右、前、上方向。利用以上参数, 分别用EKF方法和UKF方法对所建立的传递对准非线性模型(16)和(18)进行状态估计, 结果如图2~ 8所示。其中, 图8为基于EKF和UKF两种非线性滤波算法估计出的四元数计算出的相对姿态角。直观来看, 两种滤波算法估计出的主、子惯导真实载体坐标系间姿态误差四元数在20 s左右都能收敛到真实值附近, 且精度也较高, 三轴速度误差也都能在10 s左右收敛到0值附近。

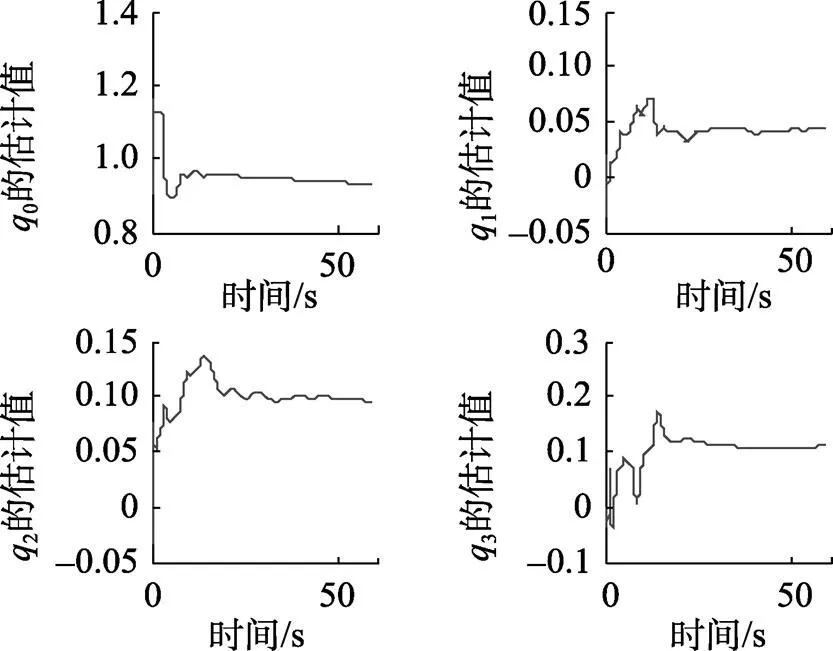
图2 基于EKF算法的主子惯导真实载体坐标系姿态误差四元数估计值

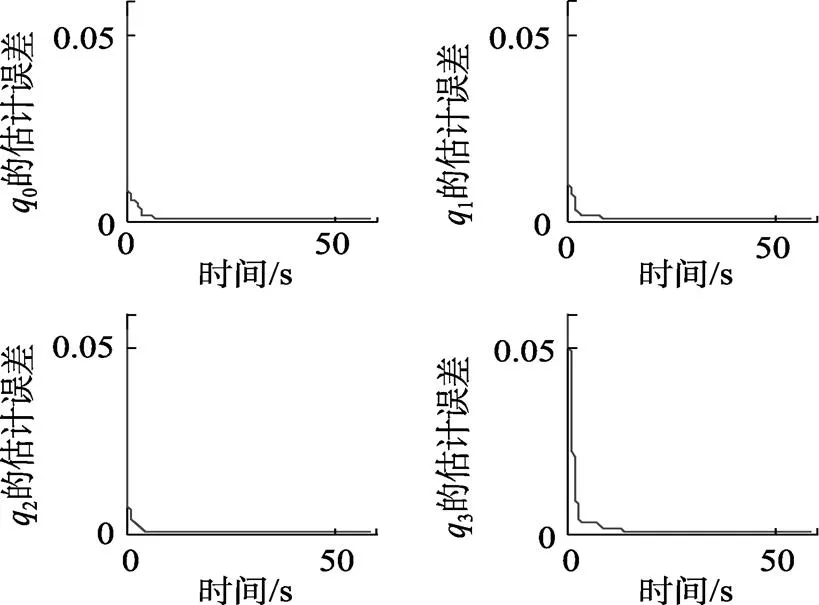
图3 基于EKF算法的主子惯导真实载体坐标系姿态误差四元数估计均方差曲线

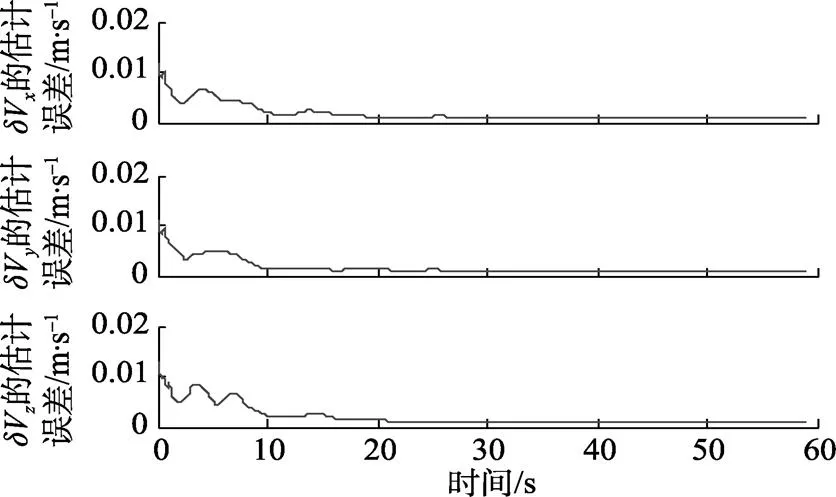
图4 基于EKF算法主子惯导速度误差估计均方差曲线

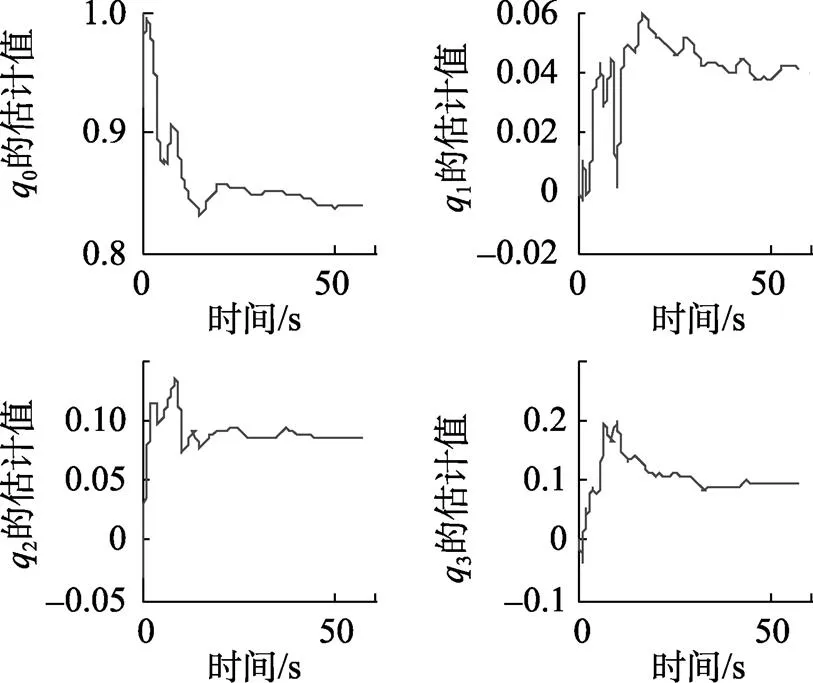
图5 基于UKF算法的主子惯导真实载体坐标系姿态误差四元数估计值

图6 基于UKF算法的主子惯导真实载体坐标系姿态误差四元数估计均方差曲线

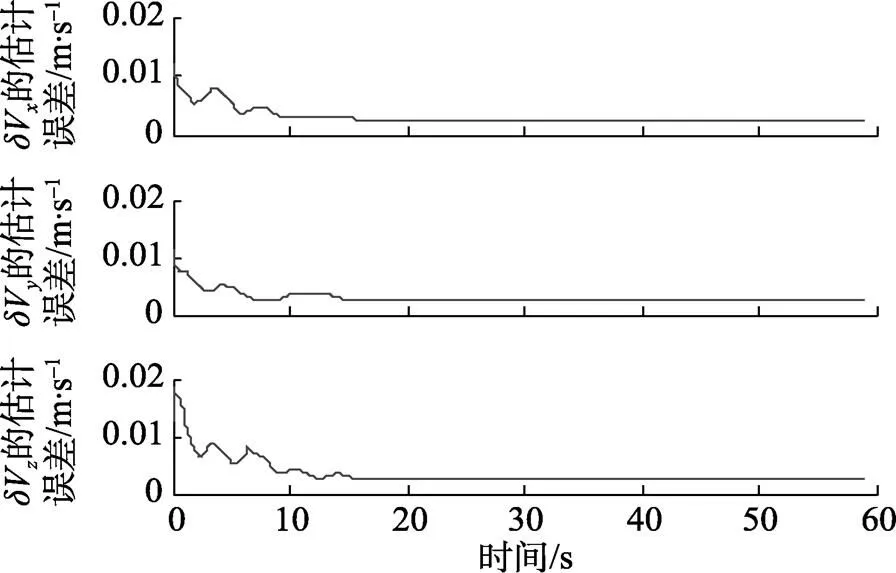
图7 基于UKF算法主子惯导速度误差估计均方差曲线

表1为应用这2种滤波方法所得主、子惯导真实载体坐标系之间姿态误差四元数估计值的标准差, 表2为2种滤波算法估计出的主、子惯导真实载体坐标系之间的姿态误差角的估计值。

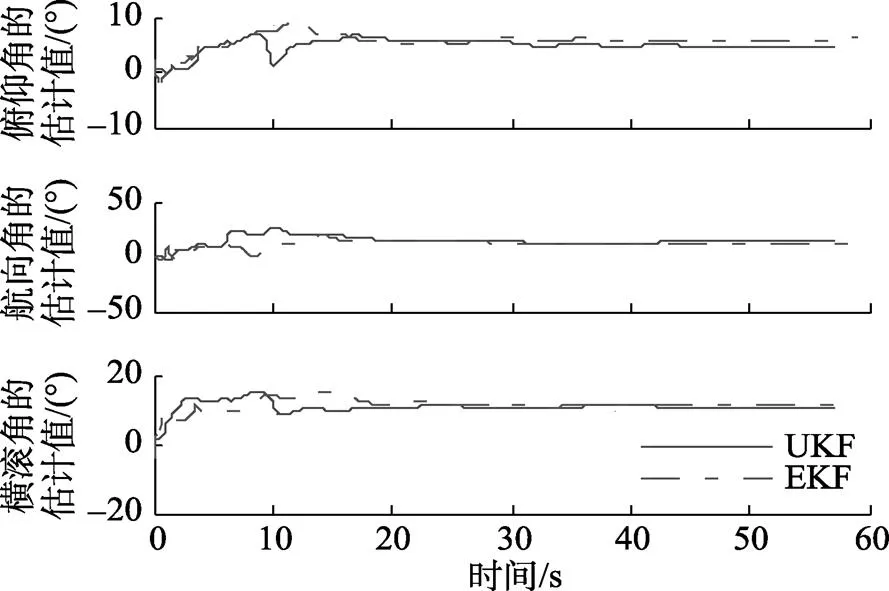
图8 基于2种滤波算法的主子惯导真实载体坐标系姿态误差角估计值

表1 基于2种滤波算法的主子惯导真实载体坐标系之间姿态误差四元数估计标准差

表2 基于2种滤波算法的主子惯导真实载体坐标系之间姿态误差角估计值

由表1看出, 应用UKF算法进行传递对准时, 主、子惯导真实载体坐标系之间的姿态误差四元数,,估计值的标准差均小于应用EKF方法进行传递对准时估计值的标准差, 而对于的估计值来说, 两种算法的估计标准差相差很小。

由表2分析得到, 基于UKF方法的姿态角估计值分别为俯仰角4.991 4°, 航向角10.685 2°, 横滚角10.021 4°, 而基于EKF方法的姿态角估计值分别为俯仰角5.468 2°, 航向角10.984 2°, 横滚角10.379 6°, 与标称值(5°,10°,10°)相比, 基于UKF算法的估计值更接近于真实值, 3个角的估计精度都大幅提高。而EKF算法由于线性化时忽略高阶项产生的误差较大而降低了滤波估计精度。从收敛性来说, 基于EKF和UKF估计的俯仰角都在大约16 s时收敛到真实值附近, 航向角在大约20 s时收敛到真实值附近, 而对于横滚角, EKF滤波在大约20 s时收敛到真实值附近, 而UKF在10 s时就收敛到真实值附近。因此, 对于舰载武器SINS传递对准非线性模型(16)和(18), 无论是收敛速度还是估计精度, UKF的滤波方法都优于EKF的滤波方法。

5 结束语

由于基于四元数的非线性传递对准模型具有计算量小、精度高、非奇异性和全姿态工作以及大角度传递对准系统设计要求等特点, 具有很强的实用性。而采用速度加姿态角的传递对准匹配方式, 只需要载体进行简单的摇摆运动即可快速完成对准, 这种匹配方式为大型载体在机动条件下实现快速对准提供了可能。因此, 对于舰载武器捷联惯导系统, 速度+姿态角匹配的传递对准方式不失为一种理想的方式, 它不需要做特别的机动动作, 只需利用舰船的自然摇摆运动就可以提高系统的可观测性, 从而提高对舰载武器SINS姿态误差角的估计速度及精度。

另外, 由于UKF非线性滤波算法与传统的EKF非线性滤波算法相比, 直接使用系统的非线性模型, 不需要对模型进行线线化处理, 也就不含有高端截断误差, 而且, UKF算法也不局限于系统或量测噪声为高斯分布的情形。仿真结果表明, 对于速度误差的估计, 2种滤波方法都能在10 s左右收敛, 且估计精度较高; 对于姿态误差估计, 无论在收敛速度还是估计精度上, UKF方法都具有较高的估计精度和较快的收敛速度。因此, 对舰载武器SINS进行传递对准时, UKF是一种值得推广应用的滤波方法。

[1] 王新龙, 申亮亮, 马闪. 摇摆基座SINS快速精确传递对准方法[J]. 北京航空航天大学学报, 2009, 35(6): 728-731. Wang Xin-long, Shen Liang-liang, Ma Shan. Transfer Align- ment of Strapdown Inertial Navigation Systems on Rolling Bases[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(6): 728-731.

[2] 秦永元, 严恭敏, 顾东晴, 等. 摇摆基座上基于信息的捷联惯导粗对准研究[J]. 西北工业大学学报, 2005, 23(5): 681-684.

Qin Yong-yuan, Yan Gong-min, Gu Dong-qing, et al. A Clear Way of SINS Coarse Alignment Design Rockong Ship[J]. Journal of Northwestern Polytechnical University, 2005, 23(5): 681-684.

[3] Julier S J, Uhlmann J K. A New Approach for Filtering Nonlinear System[C]//Proceedings of the 1995 American Control Conference, 1995: 1628-1632.

[4] 申亮亮, 王新龙, 陈涛. 舰载武器SINS速度+姿态匹配传递对准建模与仿真[J]. 鱼雷技术, 2008,16(5): 22-26.

Shen Liang-liang, Wang Xin-long, Chen Tao. Modeling and Simulation of Velocity and Attitude Matching Transfer Ali- gnment of Strapdown Inertial Navigation System for Ship- borne Weapons[J], Torpedo Technology, 2008, 16(5): 22-26.

[5] 熊芝兰, 郝燕玲, 孙枫. 基于四元数的惯导系统快速匹配对准算法[J]. 哈尔滨工程大学学报, 2008, 29(1): 28-34. Xiong Zhi-lan, Hao Yan-ling, Sun Feng. Rapid Matching Alignment Algorithm of Inertial Navigation System Based on Quaternion[J]. Jornal of Harbin Engineering University, 2008, 29(1): 28-34.

[6] 万德钧, 房建成. 惯性导航初始对准[M]. 南京: 东南大学出版社, 1999: 174.

[7] 程向红, 万德钧, 仲巡. 捷联惯导系统的可观测性和可观测度研究[J]. 东南大学学报, 1997, 27(6): 6-10. Cheng Xiang-hong, Wan De-jun, Zhong Xun. Study on Observability and Its Degree of Strapdown Inertial Navi- gation System[J]. Jouanal of Southeast University, 1997, 27(6): 6-10.

[8] Efebvre T L, Bruyninckx H, Schutter J De. Comment on “A New Method for the Nonlinear Transform of Means and Covariances in Filters and Estimators” [J]. IEEE Transactions on utomation Control, 2002, 47(8): 1406-1408.

[9] 孙昌跃, 邓正隆. 大方位失准角的舰载武器INS对准[J]. 中国惯性技术学报, 2008, 16(5): 534-537.

Sun Chang-yue, Deng Zheng-long. Alignment of Shipborne Weapon INS with Large Inertial Azimuth Uncertainty[J]. Jornal of Chinese Inertial Technology, 2008, 16(5): 534-537.

[10] Bertozzi M, Binelli E, Roggi A.Stereo Vision-based Appro- hes for Pedestrian Detection[J]. Proceeding of 2005 IEEE Comter Society Conference on Computer Vision and Pattern Recognition, IEEE, 2005, 25(25): 16-23.

[11] 邓胜利, 邵雷, 吴平. SINS/GPS全姿态组合导航系统的UKF算法研究[J]. 电光与控制, 2010, 17(12): 24-28.

Deng Sheng-li, Shao Lei, Wu Ping. The UKF Algorithm Used in All-Attitude Intergrated Navigation System of SINS/ GPS[J]. Electronics Optics & Control, 2010, 17(12): 24-28.

(责任编辑: 杨力军)

Nonlinear Transfer Alignment Model and Filtering Algorithm for Strapdown Inertial Navigation System of Shipborne Weapons

LI Na, WANG Xin-long

(School of Astronautics, Beihang University of Aeronautics and Astronautics, Beijing 100191, China)

To satisfy the requirement of fast reaction and high precision of initial alignment for shipborne weapons, and to enhance the transfer alignment for shipborne weapons with large misalignment, we present a method of combining the rapid transfer alignment model based on quaternion and the nonlinear unscented Kalman filter (UKF) algorithm, and establish a nonlinear error model for strapdown inertial navigation system(SINS) of shipborne weapons. This error model introduces quaternion to describe the attitude errors in order to enhance the speed and accuracy in calculating attitude. We select a velocity and attitude matching approach to improve the observability of the system, and solve the ill-condition of covariance matrix of the traditional nonlinear UKF filter by using singular value decomposition(SVD) to ensure the algorithm robustness. The simulation results show that the proposed method can effectively improve the precision and speed of transfer alignment for shipborne weapons with large misalignment, and its calculation accuracy and alignment time meet the design requirements of the system.

shipborne weapons; strapdown inertial navigation system(SINS); nonlinear; quaternion; unscented Kalman filter(UKF); transfer alignment

TJ630.33; TJ765.3

A

1673-1948(2011)06-0443-08

2011-05-03;

2011-06-10.

李 娜(1983-), 女, 在读硕士, 研究方向为惯性导航技术.