OFDM系统中基于限幅和压缩感知的非线性失真补偿算法
杨 霖,何向东,丁长文
(1.电子科技大学通信抗干扰技术国家级重点实验室,四川成都 611731;2.中国电子科技集团公司第五十四所通信网信息信传输与分发技术重点实验室,河北石家庄 050081)
OFDM系统中基于限幅和压缩感知的非线性失真补偿算法
杨 霖1,2,何向东1,丁长文1
(1.电子科技大学通信抗干扰技术国家级重点实验室,四川成都 611731;2.中国电子科技集团公司第五十四所通信网信息信传输与分发技术重点实验室,河北石家庄 050081)
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)信号具有较高的峰均功率比(Peak to Average Power Ratio,PAPR),不仅影响功率放大器(High Power Amplifier,HPA)的工作效率,而且HPA使得OFDM信号产生严重的非线性失真,导致系统的误比特率(Bite Error Rate,BER)增大.本文基于限幅和压缩感知(Compressive Sensing,CS)提出了改进的补偿算法,发送端采用限幅降低信号的PAPR,接收端首先采用改进的逆模型方式减小HPA引入的非线性失真,再采用CS抵消由限幅引入的信号失真.仿真表明,所提方法不仅明显降低了OFDM信号的PAPR,而且有效提高了系统的BER性能.
正交频分复用;峰均比;限幅;非线性失真补偿;压缩感知
1 引言
正交频率复用(Orthogonal Frequency Division Multiplexing,OFDM)技术以其高效的频谱利用率和抗衰落能力被广泛应用于无线通信系统中.然而,OFDM信号具有较高的峰均功率比(Peak to Average Power Ratio,PAPR)的缺点,导致经过功率放大器(High Power Amplifier,HPA)会产生带内噪声,同时会降低HPA的工作效率,带内噪声会使得信号产生严重的非线性失真,恶化系统的误比特率(Bite Error Rate,BER)性能.为了提高HPA的工作效率,降低信号的非线性失真,发送端的PAPR抑制技术和接收端的非线性失真补偿技术均是研究的热点.
发送端的PAPR抑制技术[1,2]大致可以分为三种:限幅类、编码类和概率类[3,4].其中,限幅[5,6]技术是最简单直接的,然而,限幅方式本身会额外地引入信号失真[7],恶化系统的BER性能,为了抵消限幅噪声干扰,接收端的压缩感知(Compressive Sensing,CS)算法被提出.文献[8,9]中提出了预留空子载波的CS算法,该算法需要预先保留空子载波用来作为观测向量,降低了数据传输效率.文献[10]提出了改进的CS算法,从数据子载波中选出受噪声影响较小的部分作为观测向量,利用CS算法对限幅噪声信号进行重建,该算法不需要预留空子载波,不会降低数据传输效率.但是该文仅仅考虑对限幅方法的非线性失真进行有效补偿,并没有考虑HPA带来的失真影响.另一方面,接收端的补偿技术能有效地降低HPA引入的非线性失真,文献[11]中提出了基于HPA逆模型的非线性失真补偿算法,虽然该方法能有效地改善了系统的BER性能,但是该算法需要通过多次仿真来选择合适的补偿门限,给硬件实现带来不便;且发送端并未降低OFDM信号的PAPR,HPA所需的动态范围较大,工作效率不高.为了克服上述问题,本文结合限幅、HPA逆模型补偿和CS算法,提出了改进的失真补偿算法.在发送端,采用限幅降低OFDM信号的PAPR,提高HPA的工作效率;在接收端,根据限幅门限唯一确定HPA逆模型补偿器的门限,不需要通过多次仿真来选择门限值,在补偿HPA引入的非线性失真后,通过CS抵消限幅引入的信号失真.
2 OFDM系统简介
2.1 功率放大器的影响
OFDM信号具有高峰均比的缺点,发送端的功率放大器会使OFDM信号产生严重的非线性失真,影响系统的BER性能.固态功率放大器[12](Solid State Power Amplifier,SSPA)是常用的放大器之一,Rapp模型常被用来模拟SSPA放大器的非线性特征,在该模型中,输入信号x,输出信号y的采样点表示为:
y(n)=A(|x(n)|)ej[P(x(n))+F(|x(n)|)]
(1)
其中,|·|表示求幅度,P(·)表示求相位,A(·)表示幅度响应,F(·)表示相位响应.HPA的非线性特征为:
(2)
p是平滑因子,Ao是由输入饱和Asat确定的最大输出,Asat由输入回馈(Input Back-Off,IBO)决定,即:
(3)
其中,pin表示放大器输入端信号的平均功率.
2.2 限幅和压缩感知技术
原始时域OFDM信号经过限幅后的时域信号x1采样点可表示为:
(4)
其中,A表示由限幅率γ决定的限幅门限,即:
A=γ*E{|x(n)|}
(5)
由式(4)可知,限幅后的信号x1可以表示为原始OFDM信号x和限幅失真信号c之和,即:
x1(n)=x(n)+c(n),(0≤n≤N-1)
(6)
若需利用CS技术重建限幅失真信号,失真信号必须满足稀疏性特点,由文献[10]可知,限幅率γ越低,限幅失真信号c中非零元素个数就越多,稀疏水平就越低,用稀疏度K来衡量稀疏水平,与γ的关系为:
K=E{|c|0}=N*e-γ2
(7)
接收端引入CS技术重建限幅失真信号,可以有效降低限幅失真对BER性能的影响.目前,已有很多CS算法[13]被提出,匹配追踪算法(Matching Pursuit,MP)较好地平衡了压缩感知算法效率和重构质量,正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法[14]作为MP算法中最典型的一种.
3 非线性失真补偿算法
3.1 原始HPA逆模型补偿算法
由于OFDM信号经过HPA会产生严重的非线性失真,导致系统的BER性能下降,为了降低OFDM信号的非线性失真,文献[11]中的HPA逆模型的补偿技术有效提高了系统的BER性能.补偿器的特征表达式如下:
f(r(n))=min[S,|r(n)|]
(8)
其中,A0表示放大器的饱和输出点,S表示由边沿值margin决定的最佳补偿门限,需通过多次仿真获得.
(9)
3.2 改进算法

原始的HPA逆模型补偿算法存在如下缺点:一是该算法只关注接收端,并未降低发送端OFDM信号的PAPR,较高的PAPR信号需要HPA具有较大的动态范围,降低了HPA的工作效率;二是该算法中,对于不同的仿真参数,例如子载波数、放大器的平滑因子,需要多次仿真寻找最合适的补偿门限值S,不利于硬件的实现.为了克服以上缺点,本文提出了一种基于限幅和CS的非线性失真补偿算法,原理框图如图1所示:3.2.1 发送端处理
由于PAPR较高的OFDM信号一方面要求HPA具有较大的动态范围,导致HPA的工作效率降低,另一方面HPA也会使信号产生严重的非线性失真,导致系统的BER性能下降.为了提高HPA的工作效率,降低OFDM信号的非线性失真,本文提出的算法在发送端对原始信号进行限幅处理,降低OFDM信号的PAPR,若原始频域信号为X,限幅率为γ,具体步骤如下:
步骤1 原始频域X经过IFFT变换后获得原始OFDM信号x,即:
x=WX
(10)
其中,W表示IFFT变换矩阵.
步骤2 根据式(6)可知,限幅后的时域信号x1可表示为:
x1=x+c
(11)
步骤3 限幅后的信号x1经过HPA后,HPA输出信号为x2可表示为:
(12)
其中,fHPA(·)表示HPA的非线性函数.
3.2.2 接收端处理
HPA输出信号x2经过时域信道模型后,接收信号为y,即:
y=Qx2+z
(13)
yre=Q-1y
(14)
由于限幅后的信号经过HPA仍会产生非线性失真,因此首先采用HPA逆模型补偿器对信号进行补偿,减少HPA的非线性影响,进而使用CS补偿限幅失真.本文采用改进的HPA逆模型,利用发送端的限幅门限获取唯一对应的HPA逆模型补偿器的上门限值,不需要通过仿真来选择,有利于硬件的实现,且为了降低补偿器的复杂度,增设了下门限值,其改进方法如下表所示:
表1 文献[11]中原始补偿器和所提算法补偿器门限设计方法对比

名称参数 原始HPA逆模型补偿算法改进HPA逆模型补偿算法补偿器上门限有(由多次仿真确定)有(由限幅门限唯一确定)补偿器下门限无有
改进后的HPA逆模型补偿器的特征为:
fcomp(r(n))=
(15)
其中,Adown=E{|rn|}表示补偿器的下门限,Aup表示补偿器的上门限值,由限幅门限A唯一确定,即:
(16)
经过HPA逆模型补偿后的信号y1为:
y1=fcomp(yre)
(17)
在接收端采用补偿算法后,HPA的非线性影响较小.因此采用CS算法估计出限幅噪声信号c1,即可恢复出发送端的原始时域信号y2,即:
y2=y1+c1
(18)
由2.2可知,CS技术的关键是寻找可靠的观测向量Ys和测量矩阵F,为了不影响数据传输效率,本文引用文献[10]中方法,具体步骤如下:
步骤1 根据Bussgang理论,限幅后的频域信号X1可表示为:
X1(k)=αX(k)+D(k)
(19)
其中,X(k)表示原始信号,且D(k)表示与X(k)不相关的限幅噪声;α与限幅率γ有关.且:
(20)
(21)
步骤2 利用最大似然准则估计原始频域信号Xe,即:
(22)
其中,β表示信号星座点集合,M=WHy1,WH表示FFT变换矩阵.
步骤3 由于限幅失真信号为:C=(α-1)X+D,则:
E{|C(k)|2}=(2-2α-e-γ2)E {|X(k)|2}
(23)
步骤4 根据如下式子可确定选择矩阵S:
(24)
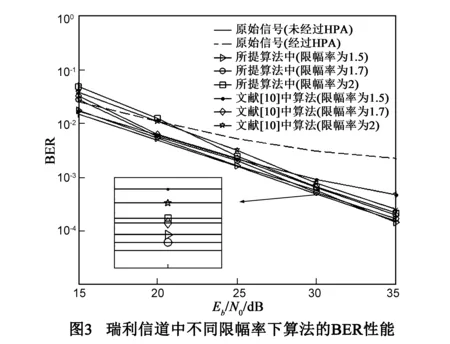
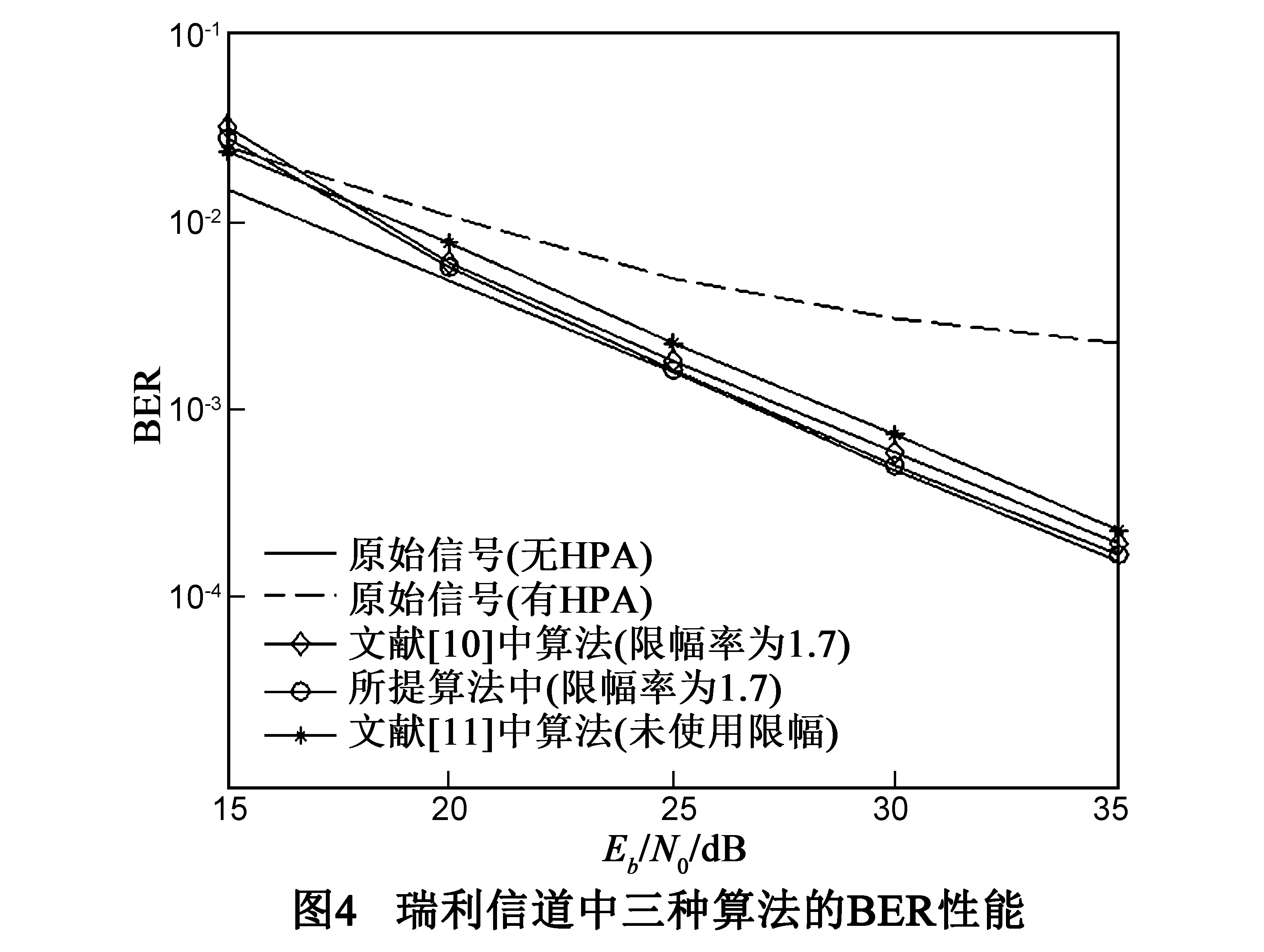
T={k:|θ1(k)|2 (25) 其中,δ2表示高斯噪声信号的方差.如果T的长度为L,那么从单位矩阵IN中选择对应的L行组成选择矩阵S. 步骤5 由选择矩阵S可获得观测矩阵Ys和测量矩阵Φ: Ys=SWHY1-SXe (26) F=SWH (27) 步骤6 根据观测矩阵和测量矩阵,运用OMP算法恢复原始信号,如算法1: 算法1 OMP算法 1 输入:(1)HPA逆模型补偿器输出信号y1;(2)观测矩阵Ys;(3)测量矩阵F;(4)稀疏度:K=N*e-γ2. 3 处理过程 (1)初始化:残差向量r0=Ys,索引Δ0=[],迭代次数t=1; (3)Δt=Δt-1∪{λt}.更新索引集; (6)估计限幅之前的时域信号:y2=y1+c1; (7)FFT变换:Y=WHy2. 一方面,限幅率影响PAPR抑制性能;另一方面,由式(10)可知限幅率决定限幅噪声信号的稀疏度和补偿器的上门限值.为了验证算法的有效性,分析了在不同限幅率γ时算法的PAPR和BER性能,参数如下 表2 仿真参数表 由式(10)可知,限幅信号的稀疏性水平K与限幅率γ相关,为了保证限幅噪声信号的稀疏性最低要求,限幅率应满足γ≥1.3,HPA的饱和点对应值为γHPA=10(IBO/10)=1.9.考虑限幅率γ在HPA饱和点内、外两种情况,本文选择限幅率γ分别为1.5、1.7和2分析了算法的PAPR抑制性能和BER性能. 4.1 PAPR性能分析 由图2可知,在三种限幅率情况下,OFDM信号的PAPR相对于原始信号均有明显降低.在CCDF=1%时,限幅率为2、1.7和1.5的限幅信号所对应的PAPR0分别为5.1dB、4.1dB和3.3dB,相对于原始信号分别降低了5.1dB、6.1dB和6.9dB.从仿真结果中可以发现,随着限幅率的减小,PAPR抑制能力越强,所需HPA的动态范围也越小,HPA的工作效率越高. 4.2 BER性能分析 在本文所提算法中,发送端采用的限幅率直接影响限幅失真信号的稀疏度,为了验证所提算法的有效性,在不同的限幅率情况下(即所需重建的限幅失真信号具有不同的稀疏度),利用瑞利信道模型分析了所提算法的BER性能,进而为所提算法选择合适的限幅门限. 图3为不同限幅率下所提算法与文献[10]中算法的BER性能,如图所示,在瑞利信道中,当限幅率较高时,在低信噪比下,本文提出的算法的BER性能稍差于文献[10]中算法,这是由于限幅率较高时所需感知的限幅噪声信号较小,低信噪比下噪声影响相对较大,且对应选取的补偿上门限未能达到最佳值,但随着信噪比大于20dB后,由于噪声影响减小,感知准确度提高,本文所提算法的BER性能逐渐优于文献[10]中算法,当信噪比为30dB时,当发送端限幅门限分别为2,1.7和1.5时,文献[10]中原始算法的BER分别为7.69×10-4,6.30×10-4和7.69×10-4;而本文所提算法的BER分别为6.59×10-4,5.17×10-4和5.59×10-4.由此可知,在存在HPA影响的情况下,使用文献[10]中算法并不能获得较优的BER性能,相对于文献[10]中算法,本文所提算法在不同限幅率(2,1.7和1.5)时,BER分别降低了1.10×10-4,1.13×10-4和2.10×10-4.此外,可以看出,不同的限幅率下所提算法的BER性能具有明显差异,当限幅率为1.7时,所提算法的BER性能较优. 图4为文献[10],[11]中算法和所提算法的BER性能比较,如图4所示,当信噪比为30dB时,未使用限幅情况下采用HPA逆模型补偿方式[11]的BER为7.46×10-4,当限幅率为1.7时,文献[10]中算法对应的BER为6.30×10-4,而本文所提算法对应的BER为5.17×10-4,由此可知,与文献[11]中算法相比,所提算法的BER降低了2.29×10-4,且由图1可知,所提算法降低了发送端信号的PAPR,有效提高了HPA的工作效率.与文献[10]中的算法相比,所提算法的BER性能降低了1.13×10-4. 原始HPA逆模型补偿算法需要通过多次仿真来选择合适的补偿门限,给实际应用带来不便,且该算法并未降低OFDM信号的PAPR,发送端HPA所需的动态范围较高,工作效率较低.本文提出的算法在发送端通过限幅方式降低OFDM信号的PAPR,接收端首先采用改进的补偿器补偿HPA引入的非线性失真后,再采用压缩感知算法抵消限幅噪声的影响.所提算法中补偿器的上门限是由发送端限幅门限唯一确定,不需要通过多次仿真获取,易于实现,且增设的下门限降低了补偿器的计算复杂度.仿真结果表明,本文提出的算法一方面有效抑制了发送端信号的PAPR,缩小了HPA所需的动态范围,提高了HPA的工作效率;另一方面良好地补偿了OFDM信号的非线性失真,提高了系统的BER性能. [1]Rahmatallah B,Mohan S.Peak-to-average power ratio reduction in OFDM system:a survey and taxonomy[J].IEEE Communications Surveys and Tutorials,2013,15(4):1567-1592. [2]Kitaek B,Powers E J.Performance analysis of OFDM systems with selected mapping in the Presence of nonlinearity[J].IEEE Transactions on Wireless Communications,2013,12(5):2314-2322. [3]Zhang Shun,GeJian-hua,Gong Feng-kui.Partial transmit sequence using EVM optimization metric for BER reduction in OFDM systems[A].IEEE Communications and Networking in China[C].Guilin:Academic Press,2013.113-117. [4]Su Yan-yong,Xue Dong,Liu Mao-cai.Combined selective mapping and extended hamming codes for PAPR reduction in OFDM systems[A].IEEE International Conference on Information Science and Technology[C].Shenzhen:Academic Press,2014.582-585. [5]Zhu Xiao-dong,Pan Wen-sheng,Li Hong,et al.Simplified approach to optimized iterative clipping and filtering for PAPR reduction of OFDM signals[J].IEEE Transactions on Communications,2013,61(5):1891-1901. [6]Shiragapur B K,Wali U,Bidwai S.Novel technique to reduce PAPR in OFDM systems by clipping and filtering[A].IEEE International Conference on Advances in Communication and Informatics[C].Mysore:Academic Press,2013.1593-1597. [7]Sudha V,Balan S,Kumar D S.Performance analysis of PAPR reduction in OFDM system with distortion and distortion less methods[A].IEEE International Conference on Computer Communication and Informatics[C].Coimbatore:Academic Press,2014.1-4. [8]Ghassemi A,Ghasemnezad H,Gulliver T A.Compressive sensing based estimation of OFDM nonlinear distortion[A].IEEE International Conference on Communications[C].Sydney:Academic Press,2014.5055-5059. [9]Masoumian S H S,Shabani M,Tazehkand B M.A new PAPR reduction method based on clipping technique using compressive sensing[A].IEEE International Symposium on Telecommunications[C].Tehran:Academic Press,2012.6-8. [10]Kim K,Park H.Clipping noise cancelation for OFDM systems using reliable observation based on compressive Sensing[J].IEEE Transactions on Broadcasting,2015,61(1):111-118. [11]Zayani R,Guedria R,Bouallegue R.Compensation of the OFDM non-linear distortion by the inverse model method[A].IEEE International Conference on Advanced Communication Technology[C].Phoenix Park:Academic Press,2006.2009-2012. [12]Al-Dalakta E,Al-Dweik A,Hazmi C.PAPR reduction scheme using maximum cross correlation[J].IEEE Communication Society,2012,16(12):2032-2035. [13]Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306. [14]Tropp J A,Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666. 杨 霖(通信作者) 男,1977年生于四川宜宾,现为电子科技大学通信抗干扰技术国家级重点实验室副教授,主要研究方向为OFDM系统中多用户检测和功率控制,OFDM系统的PAPR抑制技术等. E-mail:eelyang@uestc.edu.cn 何向东 男,1991年生于重庆,现为电子科技大学通信抗干扰技术国家级重点实验室硕士研究生.主要研究方向为现代通信中的信号处理,OFDM信号的峰均比抑制,功率放大器的非线性抑制等. E-mail:984078297@qq.com Compensation Method for Nonlinear Distortion Based on Clipping and Compressive Sensing in OFDM System YANG Lin1,2,HE Xiang-dong1,DING Chang-wen1 (1.KeyLaboratoryofNationalCommunicationTechnology,UniversityofElectronicScienceandTechnology,Chengdu,Sichuan611731,China;2.ScienceandTechnologyonInformationTransmissionandDisseminationinCommunicationNetworksLaboratory,The54thResearchInstituteofChinaElectronicsTechnologyGroupCorporation,Shijiazhuang,Hebei050081,China) The high peak to average power rate (PAPR) of orthogonal frequency division multiplexing (OFDM) signal reduced the efficiency of the high power amplifier (HPA),and led the OFDM signal suffered from nonlinear distortion caused by HPA and the bite error rate (BER) of the system became worse.This paper proposes a nonlinear distortion compensation method based on clipping and compressive sensing.The transmitter uses a clipping method to reduce the PAPR of OFDM signal;the receiver utilizes a modified method based on the inverse model of HPA to reduce the nonlinear distortion caused by the HPA,and applies compressive sensing (CS) on counteracting the distortion caused by clipping.Simulations show that the proposed method can not only reduce the PAPR of the OFDM signal significantly,but also improve the BER performance of the system promisingly. orthogonal frequency division multiplexing(OFDM);peak to average power ratio(PAPR);clipping;nonlinear distortion compensation;compressive sensing(CS) 2015-03-16; 2015-10-12;责任编辑:覃怀银 国家自然科学基金(No.61370012);国家科技重大专项课题(No.2014ZX03004003-001) TN919.3 A 0372-2112 (2016)09-2051-06 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.09.004
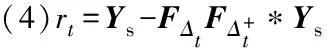

4 仿真结果与分析

5 总结



