基于传染病模型的LPA特征阀值社团划分方法
邓小龙,温 颖
(1.北京邮电大学可信分布式计算与服务教育部重点实验室,北京 100876; 2.北京邮电大学国际学院,北京 100876)
基于传染病模型的LPA特征阀值社团划分方法
邓小龙1,温 颖2
(1.北京邮电大学可信分布式计算与服务教育部重点实验室,北京 100876; 2.北京邮电大学国际学院,北京 100876)
社团结构划分对于分析复杂网络的统计特性非常重要.在非均匀社交网络的信息传播中,社团结构划分更是一个广泛关注的研究热点,相关研究往往侧重于研究紧密连接的社团结构对于信息传播所产生的关键影响.传统社团划分方法大多基于点和边的相关特性进行构建,如标签传播算法LPA(Label Propagation Algorithm)通过半监督机器学习方法,基于网络节点标签的智能交换和社团融合过程进行社团划分,但运行效率较低.为提高LPA类算法的运行速度,使其快速收敛,并提高社团划分精度,特别是重叠社团划分精度,针对LPA算法划分中的低运行效率和低融合收敛速度,本文从标签传播的网络连接矩阵本质出发,将该矩阵的最大非零特征值与网络标签信息传播的阀值相结合,提出了新的基于传染病传播模型的社团划分方法(简称ESLPA算法,Epidemic Spreading LPA).通过经典LFR Benchmark模拟测试网络、随机网络以及真实社交网络数据上的算法验证,结果表明该算法时间复杂度大幅优于经典LPA算法,在重叠社团划分上精确度优于基于LPA模型的经典COPRA算法,特别是在重叠社团较明显时,划分精度接近精度较高GA、N-cut和A-cut算法,明显优于GN、FastGN和CPM等经典算法.
重叠社团划分;流行病模型;信息扩散;最大非零特征值
1 引言
互联网的快速发展,促进了人们使用社交网站、微博、论坛、百度百科、手机呼叫网络等在线社会网络进行沟通和交流,形成了海量、复杂的社会网络结构.而社会网络中社团结构的发现对承载其上的信息传播模式探索和构建非常重要,例如社团发现对在线社交网络中研究舆情预警和口碑传播就具有重要意义.同时,随着社会网络规模的增大,节点关系愈发复杂.在真实社会网络中,企业、组织、家庭、朋友、工作伙伴等关系常交织在一个网络中,混淆了重叠社团结构的边界,使重叠社团发现变得愈发困难,给重叠社团发现提出了新的挑战,因此,研究在线社会网络的重叠社团发现方法具有重要的研究意义.
为提高LPA算法的运行效率和收敛速度,本文提出了基于传播病传播模型的LPA特征阀值社团发现算法,通过引用病毒传播模型准确定义社团重叠区域,结合病毒传播模型和网络连接矩阵的最大非零特征值定义了病毒的有限感染率传播阀值.不同于以往用固定病毒传播阀值感染整个网络,我们将感染网络中特定区域的病毒传播阀值设置为一个精确的程度域值使其只感染相同社团中的其他个体.得益于病毒传染模型里不同病毒的独立传播过程,该方法能更精确地挖掘现实情况下的重叠社团,在实验数据上获得了较高的重叠社团划分精度.此外,通过在模拟网络和真实在线社会网络数据集上进行实验,充分验证了本文所提算法的精确性和新颖性.
2 相关研究
2.1 基于标签传播的社团划分算法
社团结构(community structure)具有同社团内节点相互连接密集、异社团间节点相互连接稀疏特点,网络中真实存在的社团结构的存在使得选择社会网络中不同节点作为信息传播源头时,信息传播的速度和效率存在差异,在社团结构内部,信息的传输效率和速度往往优于社团结构之间的传播效率.
LPA算法[1]最初由Zhu等在2003年提出,执行复杂度低且分类效果好,时间复杂度为o(n2)(n为网络节点个数).基本思路是用已标记节点的标签去预测未标记节点的标签(边表示两个节点的相似度).节点标签按相似度传递给其他节点,节点间相似度越大,标签越易传播.当标签传播迭代结束,相似节点的标签分布趋于相似并被划分到同一个类别.LPA执行归纳为节点初始标签分配、迭代和社团融合完成三阶段,最后阶段需对结果进行确认和反复迭代.
2007年Raghavan等将LPA算法应用到社团结构划分,提出了与网络规模成正比的近似线性增长RAK算法[2],通过预先定义目标函数简化LPA的迭代复杂度,利用网络结构作为指导来探测社区结构.RAK在空手道俱乐部网和美国大学橄榄球网的实验结果表明,其社区检测效果良好,但在LFR benchmark网络上实验结果存在一定缺陷.此后,很多研究者改进了RAK.2010年Gregory对RAK进行了改进,提出侧重于挖掘重叠社团的COPRA算法[3](Community Overlap PRopagation Algorithm),COPRA可使单个节点保留若干个社区标签,传播过程包括多社区信息.COPRA能有效检测重叠社区,但会导致每次迭代时间增加,当重叠社区太多时,会导致不正确的标签随机选择,只对规模较小的重叠社区发现较为有效.
在大规模网络社团划分方面,2011年金弟等[4]针对传统LPA算法时间复杂度和搜索能力的缺陷,提出基于局部探测优化的近似线性快速LPA遗传算法FNCA,发现LPA 经五次迭代后,95%节点已正确聚集;后面的迭代只对社区内节点更新,是不必要的,改进了迭代结束条件.2011年Cordasco等[5]提出半同步LPA算法,通过网络顶点并行着色,结合同步和异步模式提高了运行效率,适用于大规模网络.
但是以上算法在异质、多源重叠社团的发现上迭代次数较高,算法运行时间较长,因此需构建效率更高算法提升运行效率,并防止算法陷入局部优化陷阱.
2.2 传染病传播模型
信息传播领域的经典传播模型是将现实中的传染病传播进行抽象和建模所得,早在1760年Daniel Bernoulli就用数学方法研究过天花传播.20世纪初有学者开始对确定性传染病模型进行研究,1927年William研究伦敦黑死病时,提出了SIR模型[6],后来考虑重复感染,于1932年提出了SIS模型[7].近年来,2012年张彦超和顾亦然[8]等根据真实在线社交网络中谣言的传播特点以及有疾病潜伏期的传染病模型,研究了在线社交网络中用户状态和信息传播模型,对其进行了模型逼真模拟,提出新的基于在线社交网络的谣言传播SEIR模型[9],该模型比较符合真实在线社交网络的传播特性.
但是这些模型并未考虑信息传播者被感染后又痊愈的概率,也未从整个网络的传染持续性来考虑,因此本文选择了2003年Wang[10]的传染病模型并在其上构建了重叠社团划分算法.该模型系统研究了网络谱半径和传染持久性的关系,采用比以往模型更精确、定义更优的阀值,更适用于重叠和庞大网络,应用于检测网络而不需要考虑网络拓扑结构,其具体定义将在3.3节中叙述.
3 基于传染病模型的社团划分算法
本文在Leskove等[11,12]研究成果基础上,结合信息传播的相关定义和假设,以及病毒传播的网络谱半径等重要参数模型,构建了基于传染病模型的重叠社团划分算法ESLPA.
3.1 传染病传播模型定义
2003年Wang[10]等提出传染病模型,将人与人间的感染关系抽象为有权有向网络图:G=(N,E)(N是节点集合,E是边集合),假设网络所有节点感染率(定义为β)是相同的,每个节点消除自身病毒的治愈率也相同(定义为δ).

表1 传染病模型符号定义
在上述假设的用时间戳t定义的离散时间序列中,已被感染的节点i在随后每个时间间隔内,都尝试去感染它的邻居(感染一个邻居节点成功的概率为β),同样,节点i在某时间间隔中自愈概率为δ.我们定义在时刻t时节点i被感染的概率为pi,t,同样,在时刻t节点i未受邻居节点感染,不被感染的概率为ζi,t,定义如下:
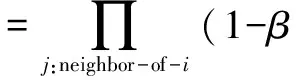
(1)
假设在某个时刻t,存在以下三种情况之一,则节点i是健康的,假如:
情况1 节点i在时刻t之前是健康的,并且没有被它的邻居节点所感染(由ζi,t定义);
情况2 节点i在时刻t之前已经被感染,在时刻t被治愈了,并且没有被它的邻居节点所感染(由ζi,t定义);
情况3 节点i在时刻t之前已被感染,在时刻t前受到了邻居节点的感染,但是该感染对节点i没有奏效,且节点i最终在时刻t被治愈了.
依据上述定义,假设某节点i被其邻居感染,但被治愈的概率为50%,那么可定义该节点的健康概率为:
1-pi,t= (1-pi,t-1)ζi,t+δpi,t-1ζi,t+0.5
×δpi,t-1(1-ζi,t)
(2)
式(2)中,i的取值范围是是从1到N,(1-pi,t-1)ζi,t、δpi,t-1ζi,t和0.5×δpi,t-1(1-ζi,t)分别对应上面定义的三种情况.当某特定网络中感染概率β和自愈概率δ都赋值后,可计算出pi,t,并据式(3)可得时刻t时网络中所有被感染节点所占比例ηt,其中N为网络中所有节点个数:
(3)
3.2 权重平衡算法WEBA
权重平衡算法WEBA(Weight-Balanced Algorithm)用于定义某个节点对于其所属社团的重要性权值[13],对于包含N个节点和m条边的无向图G=(N,E)而言,定义互不相连的L个核心节点(即Kernel)子集{K1,…,KL},对于网络所有边组成的集合E⊆V×V(|E|为所有边的条数),满足:
∀i,∀u∈Ki,∀v∉Ki,
|E(u,Ki)|≥|E(v,Ki)| and |E(Ki,u)|≥|E(Ki,v)|,
where |E(A,B)|={(u,v)∈E,u∈A,v∈B},
for {A,B⊆V}
(4)
接着定义节点的权重向量ω(ν)如下:
ω(ν)={ω1(ν),…,ωL(ν)},ν∈V
(5)
ωL(ν)是节点i对于其所属社团核心的重要性权重.据WEBA算法可计算和排序不同节点的ωL(ν)值得到社团核心节点序列,对于某给定整数值k(假设k为Kernel中节点个数),计算排序不同节点的操作变为如下优化问题[14]:
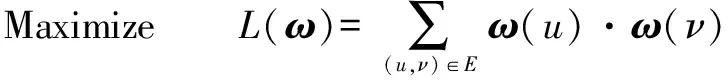

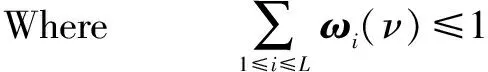
ωi(ν)≥0,∀ν∈V,∀i∈{1,…,L}
(6)
当式(6)计算完毕得到L(ω)的全局最大值,WEBA算法会收敛,可得全图核心节点序列.
3.3 基于传染病模型LPA重叠社团划分算法
本文所提基于传染病模型的ESLPA高效重叠社团划分算法构建基于“社团”定义的一个默认常识[15],即当社团内部的某个节点被病毒所感染后,相对于社团外部的节点而言,在社团内部该节点影响其他节点感染病毒的速度更快,该过程可模拟某些网络舆情信息在社团内部传播比社团外部传播更快的现实情况.
在线社交网络符合幂律分布,社团内连接边数远多于该社团和外部连接边数,因此病毒在社团内更容易快速传播,感染病毒的节点越是处于“核心节点”地位,其被感染和传播病毒的速度越快,并更易将病毒传播至整个网络.
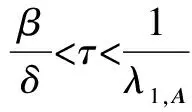
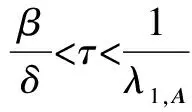
本文所提方法首先用种子病毒感染由RAK算法[2]划分所得社团和WEBA算法检测出的社团核心节点后,社团被定义为受相同病毒感染的节点群,然后模仿病毒传染过程,其他社团成员以被感染的模式展示出来,快速得到最终较精确的社团划分结果.本文所提基于传染病模型的LPA高效重叠社团划分算法步骤如下:
(1)采用Raghavan的RAK算法[2]进行初步的社团划分,获得较粗的社团分布情况;
(2)在这些初步划分所得社团,用WEBA算法计算得到这些社团的核心节点序列[13];
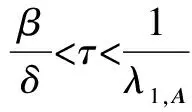
(4)最终感染过程收敛,并获得最终社团划分结果.
4 实验结果
4.1 实验环境
处理器:Intel(R) Pentium(R) 4,3.0GHz;内存:2GB;硬盘:160GB;操作系统:Windows XP;编译环境:Matlab R2010和JDK1.7.
4.2 LFR Benchmark网络数据集实验结果
我们选取了在社区发现方面被广泛采用的LFR(Lancichinetti Fortunate Radicchio)Benchmark网络程序[16]来生成基准模拟网络数据.LFR 能够灵活生成高质量的测试网络数据,LFR网络生成时可包含真实网络所具有的统计特性,例如真实网络中度分布不均匀性和社团大小分布的不均匀性等.实验共生成4组测试网络,为保证实验结果的准确性,每组网络均用本文所提ESLPA算法和经典COPRA算法[3]测试了20次,取其平均值作为实验结果.
由于存在重叠社团,故未选用模块度(Modularity)作为算法评测标准,而是选用了重叠社团发现中常被采用的规范化互信息[17](NMI,Normalized Mutual Information)作为评测标准.NMI标准由Danon等2005年提出,用于衡量算法划分的社区结构和预先已知社区结构间的差异[17].NMI基于混合矩阵(confusion matrix)M计算,如式(7)所示:
(7)
式(7)中,Ni表示M中第i行元素的总和,Nj表示M中第j列元素的总和.NMI指标可衡量划分出的社区结构与已知网络社区结构的差异,该值越大,则表明获得的社区结构划分越好,NMI达到最大值1时,说明算法发现的社区结构与已知社区结构完全一致.
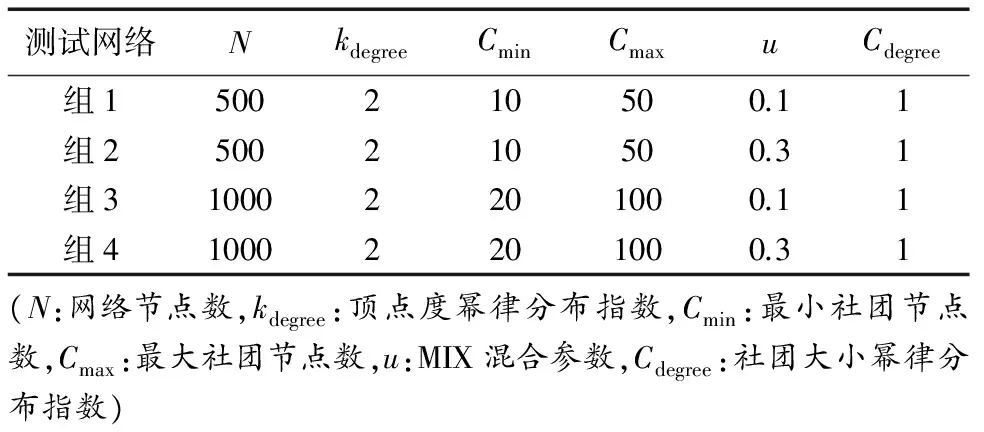
表2 LFR测试网络实验数据集
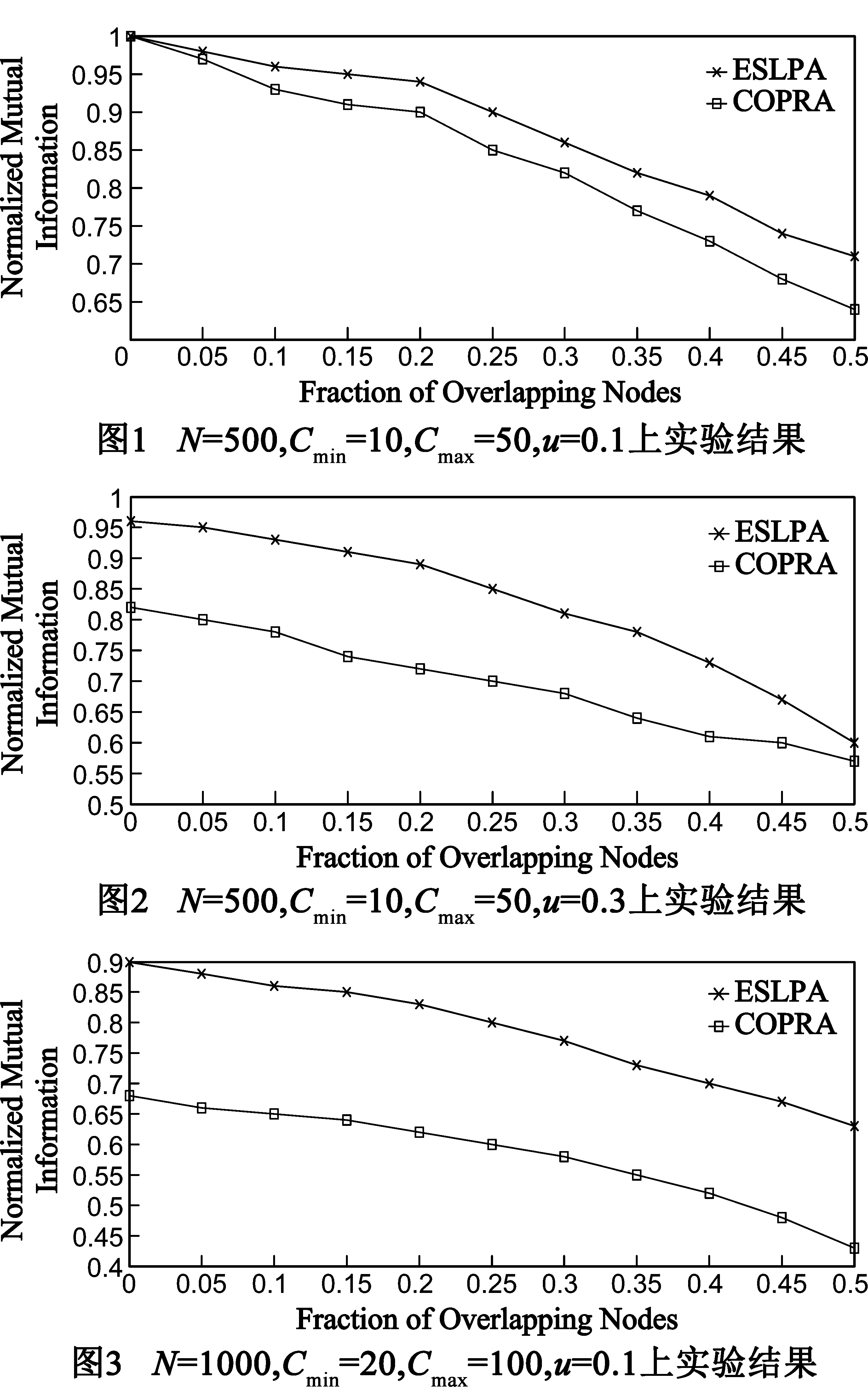
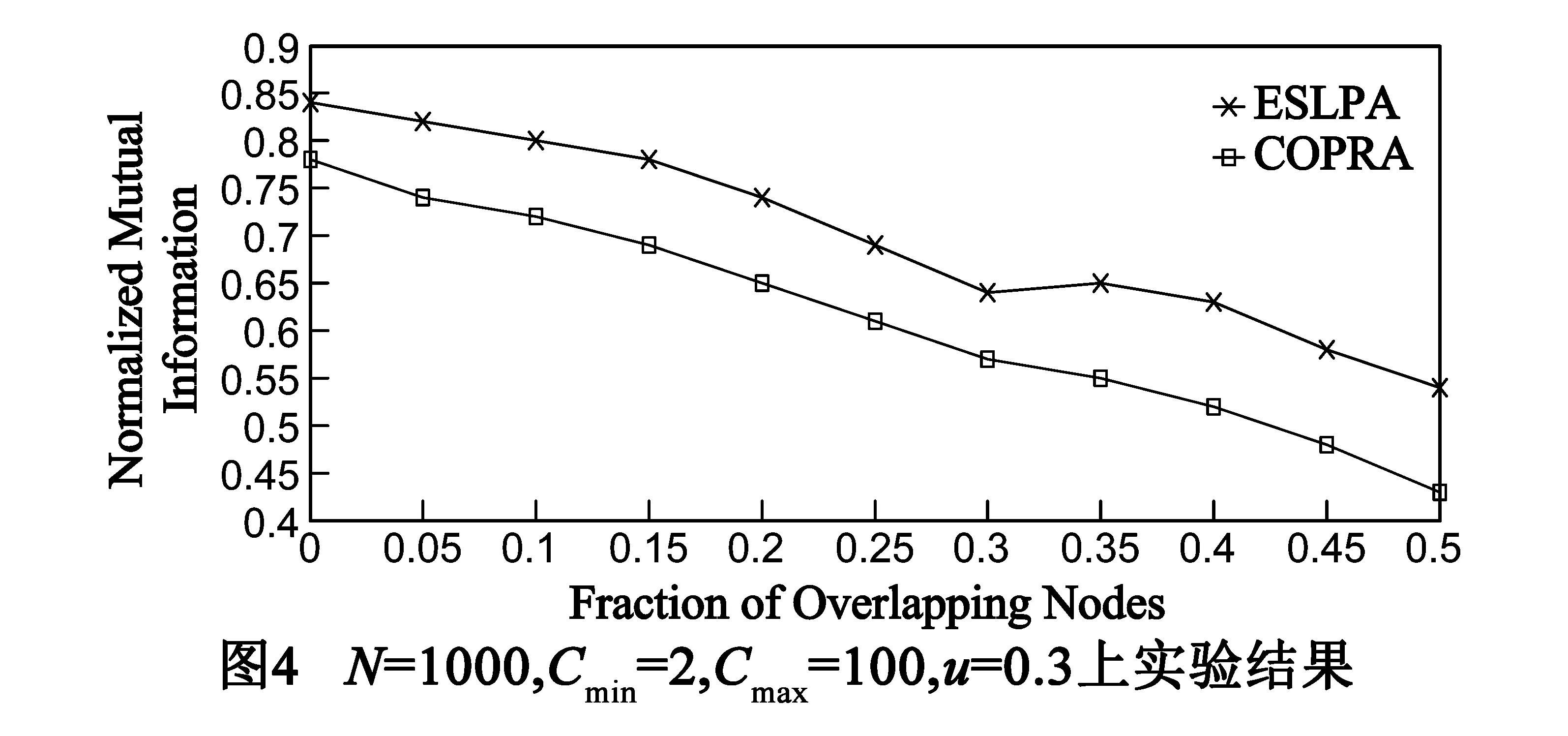
图1至图4给出了ESLPA算法和COPRA算法[3]在表1所示的4组LFR Benchmark网络程序上的实验结果,图中的y-轴表示划分结果中的NMI结果数值,x-轴表示网络中位于重叠社团的节点比例.从图中显示结果可知,ESLPA算法在NMI数值上比COPRA算法结果要好,划分结果更为精确,并且随着MIX混合参数的数值变大,两种算法的划分精度差距减小.
4.3 随机网络数据集实验结果
划分精度和划分速度是评价社团划分算法性能的重要指标,我们给出了ESLPA算法和其他典型社团算法在这两个维度上的实验结果,作为定量比较和评价各算法性能的重要依据.实验数据集选取了广泛采用的已知社团结构随机网络测试法[15],在该方法中,已知社团结构的随机网络定义为(C,s,d,Pin)[15],其中C表示网络社团的个数,s表示每个社团包含节点的个数,d表示网络中节点的平均度,Pin表示社团内连接密度(即社团内连接总数与网络连接总数的比值).Pin值越大,随机网络的社团结构越明显;反之社团结构越模糊.特别地,当Pin<0.5时,认为该随机网络不具有社团结构.一个随机网络被正确划分当且仅当预定义的C个网络社团被全部正确识别,且没有某个社团被进一步分割为多个子社团.
4.3.1 划分精度比较
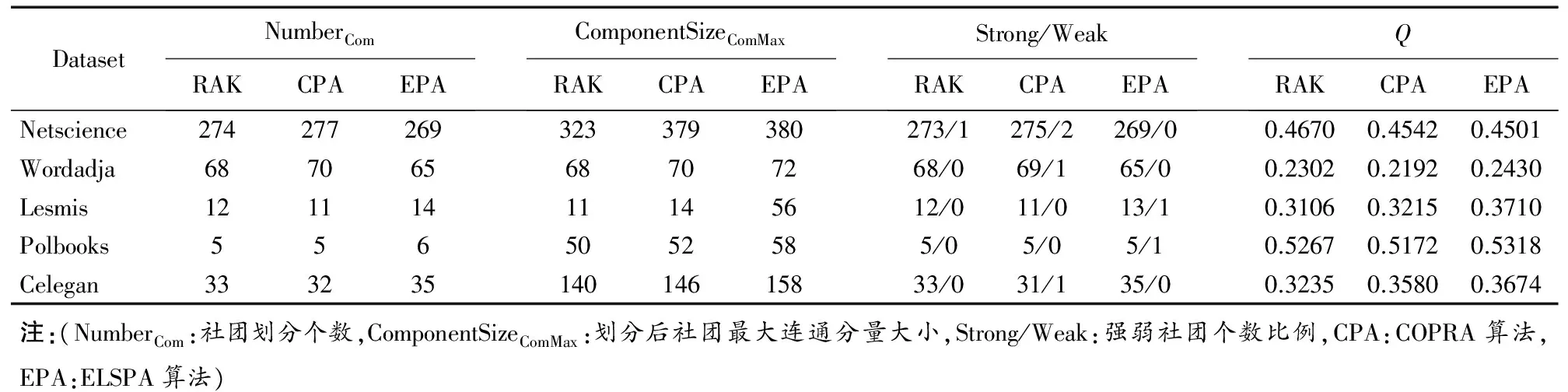
目前社团划分大致可分为基于优化的划分方法和启发式划分方法[18],我们分别从基于优化的划分方法和启发式划分方法中选择了具有代表性的七种算法GN、FastGN、GA、FEC、N-Cut、A-Cut和CPM(算法源代码来自文献[18])和侧重于挖掘重叠社团的经典COPRA算法[3]进行了比较.图5给出了本文ESLPA划分算法和其他七种典型算法划分精度比较的实验结果,这里选取了被普遍采用的基准随机网络RN(4,32,16,Pin).在图5中,对应于x-轴上的每个Pin数值都生成了一组含100个随机网络的数据集(随机网络通过实现文献[18]中介绍的算法批量生成,一共生成了12组),y-轴表示划分精度.划分精度曲线上的每个数据点是该算法划分100个随机网络得到的平均准确率.
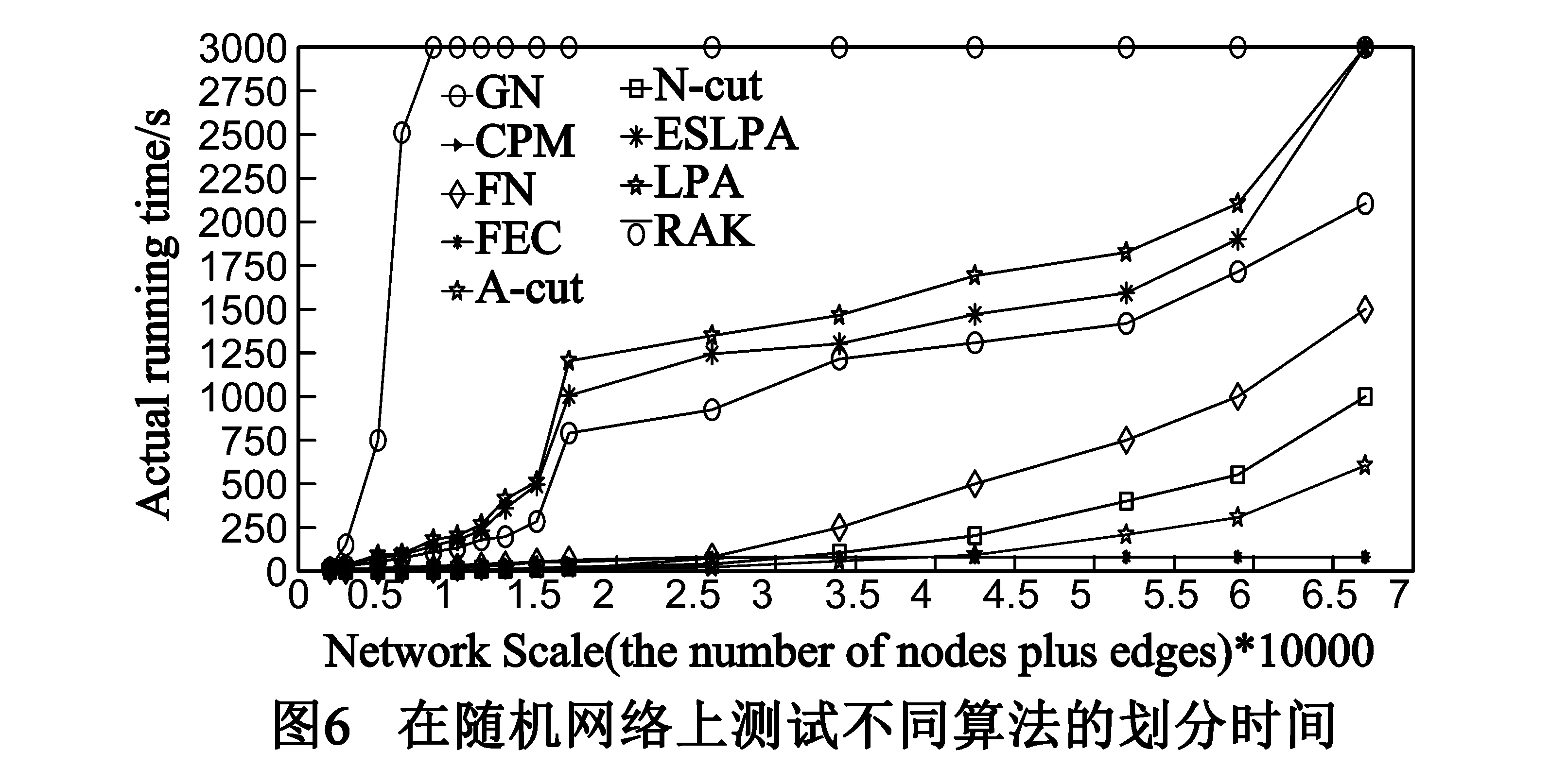
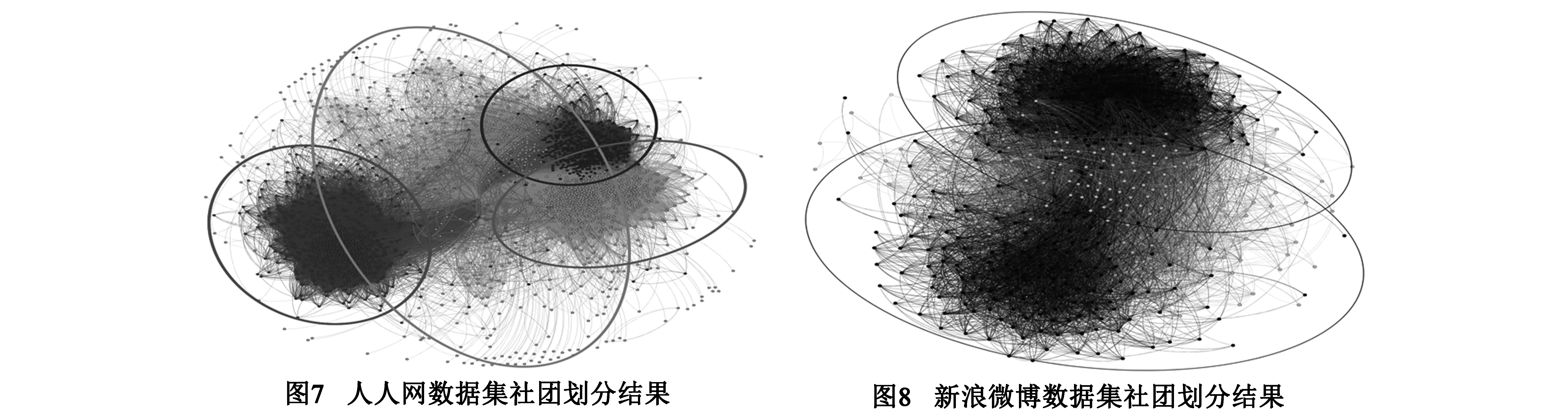
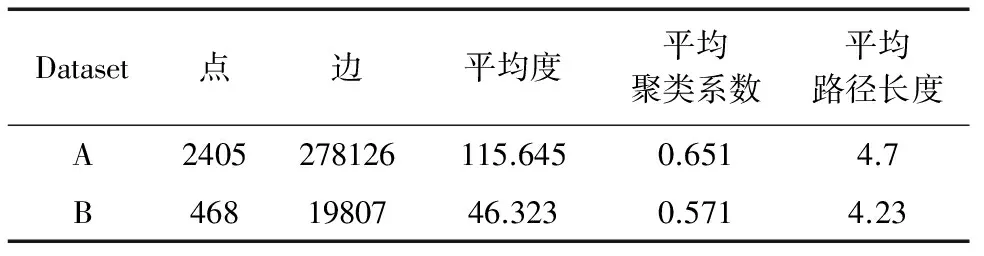
由图5分析可知:(1)ESLPA算法在Pin<0.5存在重叠社团时,划分精度略低于计算复杂度非常高的GA算法、N-cut算法和A-cut算法,但是明显优于COPRA算法、FastGN算法(图5中的FN曲线)和CPM算法;(2)在0.5 由图5可得结论:在重叠社团的划分精度上ESLPA算法优于COPRA算法,特别是在重叠社团较明显时(Pin<0.55),划分精度甚至接近时间复杂度非常高的GA算法、N-cut算法和A-cut算法,明显优于GN算法、FastGN算法和CPM算法等经典算法. 4.3.2 划分速度比较 图6实验结果给出了ESLPA算法和其他八种经典社团划分算法在划分速度上的时间复杂性比较(由于GA算法时间复杂度太高[18],故未和它进行比较),其中包含经典LPA和经典RAK算法[2],实验结果给出了各算法的实际运行时间,作为比较和评价各算法性能的重要依据.本实验采用随机网络RN(4,s,16,0.7)作为测试网络.该网络社团结构确定,规模可由s值调节,共包括4s个网络节点,64s条边.图6中,y-轴表示以秒为单位的算法实际运行时间,x-轴表示被测试网络的网络规模(节点数+边数). 分析图6所示实验结果可知,ESLPA算法的计算速度在经典的LPA和RAK算法之间,相对于经典LPA算法的运行时间,有较明显改善.从时间复杂度o(n2)(n是网络中节点的个数)来衡量,其运行速度明显快于GN(时间复杂度接近o(n3)),从整体上来说,均属于启发式算法的LPA、ESLPA、RAK、FEC和CPM算法,其实际运行时间与网络规模呈近似线性比例关系,运行较快,其次是两种谱方法N-Cut和A-Cut. 4.4 真实在线社交网络数据集实验结果 为验证ESLPA算法在真实社交网络上的划分效果,我们依据Leskove等[11]数据采集方法,采集了某个已知大三学生人人网交友圈的真实社交网络(表3中数据A).另一个真实社会网络数据来自新浪微博(表3中数据B),数据A和B均为典型小世界网络.图7所示划分结果与该学生的真实社团结构保持了一致,结果准确显示了该学生所在的4个社团:高中、大一、大二和大三同学,最大重叠模块密度为7.2541.图8所示划分结果显示该网络被划分为两个重叠社团,最大重叠模块密度为6.8975,也与真实情况相符,以上两个实验结果显示了ESLPA算法在大型在线社交网络上的较好性能. 表3 真实社交网络数据集 Dataset点边平均度平均聚类系数平均路径长度A2405278126115.6450.6514.7B4681980746.3230.5714.23 4.5 真实重叠网络数据集实验结果 为检测ELSPA算法在具有重叠的不确定社团结构的真实网络上的性能,选择了具有重叠社团的经典数据集,选取了 Newman个人网站(www.personal.umich.edu/~mejn/netdataGirvan)上的部分标准数据集Netscience、Wordadja、Lesmis、Polbooks和Celegan等.采用近年被多次引用的网络社团轮廓方法(Network Community Profile,NCP)[11],选取Q值、社团划分个数、划分后社团最大连通分量大小以及强弱社团个数比例[11]4个参数比较了代表性的LPA类算法RAK、COPRA和本文ELSPA算法的性能,实验结果如表4所示. 通过分析表4可知:在这4个网络数据集上,本文所提ELSPA算法的Q值非常接近RAK和COPRA算法,但是在强弱社团比和社团最大连通分量大小两个指标上ELSPA算法数值优于RAK和COPRA,所得社团结构节点数更多,社团结构更明显,可见其划分效果更好. 表4 真实网络社团结构划分性能实验结果 群体中的个体具有更加密集的联系和较高概率的相互信息传播,本文针对LPA算法运行速率低和融合收敛慢的缺点,提出了一种通过定义网络核心节点和网络连接矩阵非零最大特征值阀值,利用传播病毒模型来发现社团结构的新方法.通过经典LFR Benchmark模拟测试网络、随机网络、真实网络(含社交网络和非社交的重叠网络)数据上的算法验证,表明该算法时间复杂度大幅优于经典LPA算法,在重叠社团划分上精确度优于基于LPA模型的经典COPRA算法,特别是在重叠社团较明显时,划分精度接近精度较高GA、N-cut和A-cut算法,明显优于GN、FastGN和CPM等经典算法. 后续研究将如下展开:(1)进一步调整算法中病毒传播模型用于特定需求的社团发现;(2)进一步地研究病毒在带有不同特点的个体间具体传播过程,通过病毒传播模型来发现具有不同兴趣的多种异质社团. [1]ZHU X,Ghahramani Z,Lafferty J.Semi-supervised learning using Gaussian fields and harmonic functions[A].Proceedings of the Twentieth International Conference on Machine Learning[C].Washington DC,USA:AAAI,2003.912-919. [2]Usha Nandini Raghavan,R′eka Albert,Soundar Kumara.Near linear time algorithm to detect community structures in large-scale networks[J].Physical Review E,2007,76(3):036106,1-11. [3]Steve Gregory.Finding overlappingcommunities in networks by label propagation[J].New J Phys,2010,12(10):103018,1-26. [4]金弟,刘大有,等.基于局部探测的快速复杂网络聚类算法[J].电子学报,2011,39(11):2540-2546. Jin Di,Liu Dayou,et al.Fast complex network clustering algorithm using local detection[J].Acta Electronica Sinica,2011,39(11):2540-2546.(in Chinese) [5]Cordasco G,Gargano L.Community detection via semi-synchronous label propagation algorithms[A].Proceedings of 2010 IEEE International Workshop on Business Applications of Social Network Analysis[C].Bangalore,India:IEEE Computer Society,2010.45-50. [6]William O Kermack,Anderson G McKendrick.Contributions to the mathematical theory of epidemics,part I[J].Proceedings of the Royal Society of London,Series A,1927,115(772):700-721. [7]William O Kermack,Anderson G McKendrick.Contributions to the mathematical theory of epidemics,part II.The problem of endemicity[J].Proceedings of the Royal Society of London,Series A,1932,138(834):55-83. [8]顾亦然,夏玲玲.在线社交网络中谣言的传播与抑制[J].物理学报.2012,61(23):238701,1-7. Gu Yi-Ran,Xia Ling-Ling.The propagation and inhibition of rumors in online social network[J].Acta Phys Sin,2012,61(23):238701,1-7.(in Chinese) [9]王超,杨旭颖,等.基于SEIR的社交网络信息传播模型[J].电子学报,2014,11(1):2325-2330. Wang Chao,Yang Xuying,et al.SEIR-based model for the information Spreading over SNS[J].Acta Electronica Sinica,2014,11(1):2325-2330.(in Chinese) [10]Yang Wang,Deepayan Chakrabarti,Chenxi Wang.Epidemic spreading in real networks:An eigenvalue viewpoint[A].Proceedings of 22nd Symposium in Reliable Distributed Computing[C].Florence Italy:Institute of Electrical and Electronics Engineers Computer Society,200.25-34. [11]Jure Leskovec,Kevin J Lang,Michael W.Mahoney.Empirical comparison of algorithms for network community detection[A].Proceedings of WWW ACM 2010[C].Raleigh,NC:Association for Computing Machinery,2010.631-640. [12]R Pastor-Satorras,A Vespignani.Epidemic dynamics infinite size scale-free networks[J].Physical Review E,2002,65(3):035108,1-4. [13]Liaoruo Wang,Tiancheng Lou,Jie Tang,John E Hopcroft.Detecting community kernels in large social networks[A].Proceedings of 2011 IEEE 11th International Conference on Data Mining[C].Vancouver,BC,Canada:Institute of Electrical and Electronics Engineers Inc,2011.784-793. [14]Michael R Garey,David S Johnson.Computers and Intractability :A Guide to the Theory of NP-Completenes[M].San Francisco :W HFreeman Company,1979.90-194. [15]Girvan M,Newman MEJ.Community structure in social and biological networks[J].Proceedings of the National Academy of Sciences,2002,99(12):7821-7826. [16]Andrea Lancichinetti,Santo Fortunato,Filippo Radicchi.Benchmark graphs for testing community detection algorithms[J].Physical Review E,2008,78(4):046110,1-5. [17]Leon Vicsek Danon,Jordi Duch,Alex Arenas,Albert Diaz-Guilera.Comparing community structure identification[J].Journal of Statistical Mechanics Theory & Experiment,2005,09:P09008,1-10. [18]杨博,刘大有,等.复杂网络聚类方法[J].软件学报,2009,20(1):54-66. Yang Bo,Liu Dayou,et al.Complex network clustering algorithms[J].Journal of Software,2009,20(1):54-66.(in Chinese) 邓小龙 男,1977年10月出生,湖北沙市人,博士,北京邮电大学教师、硕导,主要研究领域为社交网络,数据挖掘. E-mail:shannondeng@bupt.edu.cn 温 颖 男,1994年8月出生,江西赣州人,北京邮电大学硕士研究生,主要研究领域为社会计算,复杂系统动力学. E-mail:wenying@bupt.edu.cn Efficient Epidemic Spreading Model Based LPA Threshold Community Detection Method DENG Xiao-long1,WEN Ying2 (1.KeyLabofTrustworthyDistributedComputingandServiceofEducationMinistry,BeijingUniversityofPostandTelecommunication,Beijing100876,China; 2.DepartmentofInternationalSchool,BeijingUniversityofPostandTelecommunication,Beijing100876,China) Community detection method is significant to character statistics of complex network.Community detection in inhomogeneous structured network is an attractive research problem while most previous approaches attempted to divide networks into communities which are based on node or edge measurement.The label propagation algorithm (LPA) adopts semi-supervised machine learning and implemented community detection in an intelligent way with automatic convergent process of network node label iteration but it often results in low efficiency in the final convergent process.In this article,aiming to promote low efficiency and stagnant converging rate of LPA in network with overlapping communities,we propose a new method (ESLPA) for community detection using epidemic spreading model combined with network connection matrix’s largest Eigenvalue as label propagation threshold.Extensive experiments in synthetic signed network and real-life large networks derived from online social media are conducted to explore optimal mechanism of the most suitable community detecting virus infection threshold.Experiments result prove that our method is more accurate and faster than several traditional modularity based community detection methods such as COPRA,GN,FastGN and CPM. overlapping community detection;Epidemic model;information spreading;largest eigenvalue 2015-02-12; 2015-06-05;责任编辑:梅志强 国家973重点基础研究发展计划(No.2013CB329600);“十二五”国家科技支撑计划国家文化科技创新工程(No.2013BAH43F01);国家自然科学基金(No.91024032) TP391 A 0372-2112 (2016)09-2114-07 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.09.014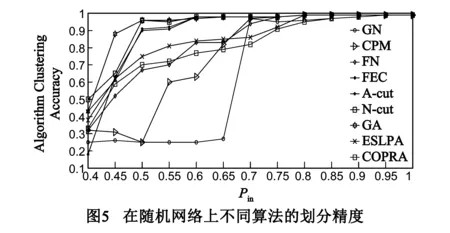
5 结束语



