一种基于稀疏约束的稳健波束形成方法
解 虎,冯大政,袁明冬
(1.中国空间技术研究院西安分院西安,陕西西安710100;2.西安电子科技大学雷达信号处理国家重点实验室,陕西西安710071)
一种基于稀疏约束的稳健波束形成方法
解 虎1,2,冯大政2,袁明冬2
(1.中国空间技术研究院西安分院西安,陕西西安710100;2.西安电子科技大学雷达信号处理国家重点实验室,陕西西安710071)
通过分析最优自适应波束形成权矢量的子空间组成,发现最优权仅位于低维的干扰加信号子空间中.一般系统所要抑制的干扰数目远小于系统自由度,因此一旦估计出干扰空间和信号导向矢量,只需求解一个低维的组合矢量即可求得自适应权矢量,同时也极大地降低了计算复杂度.本文首先构造一个完备的干扰加信号子空间(IPSS),然后对组合矢量进行稀疏约束,找到一组列数最小的信号加干扰子空间来构造自适应权.仿真实验验证了所提算法的有效性和稳健性.
稳健波束形成;稀疏约束;导向矢量失配;正则化;凸优化
1 引言
波束形成(BeamForming,BF)一直以来都是阵列信号处理的热点问题之一,被广泛应用于雷达、声纳、语音麦克风阵列[1,2,4]、无线通信[3]等领域.波束形成的基本思想[4,5]是使信号方向增益保持恒定的同时对来自其他方位的强干扰进行自适应抑制.传统的波束形成针对的是期望信号导向矢量准确已知且对应的协方差矩阵不存在估计误差.而实际中,导向矢量不匹配、样本较少导致估计的协方差矩阵不准确、接收数据包含较强的期望信号[1,6,7]等都会对波束形成的性能产生影响.针对这一问题,学者们提出了针对不匹配情况下的稳健波束形成方法,使得在存在各种不匹配时,算法性能不会严重下降.稳健波束形成在实际应用中发挥着重要的作用,目前已经成为学者们的研究热点.
对角加载技术(Diagonal Loading,DL)是一种公认的行之有效的稳健波束形成方法,对阵列流形不匹配和小样本环境都具有很好的稳健效果,但是当接收信号中存在期望信号时,会产生信号对消现象,导致算法性能严重下降.另一方面,关于如何选取的最优的加载量目前尚没有统一的定论.文献[8]提出了一种基于最差环境下的稳健BF方法,该方法假设阵列流形误差属于一个球形不确定集,并对目标导向矢量加以约束,并采用最小方差无畸变准则(Minimum Variance Distortionless Response,MVDR)加以推导,将非凸问题转化为二阶凸优化(Second Order Cone Program,SOCP)问题加以求解.已经证明该算法本质上属于DL类方法,其加载量由误差上界确定.文献[9]将球形不确定集推广到椭球不确定集,并且提出一种直接求解对角加载量的方法,避免了求解SOCP问题.文献[10]提出一种采用l1范数近似的方法来计算加载量.子空间方法是另外一类稳健BF方法,对多种不匹配情况均有稳健作用.
针对目标导向矢量不匹配导致的波束形成性能损失问题,学者们提出了许多对应的稳健方法,文献[11]提出一种约束目标方位角度一定范围内的方向的增益大于1的稳健波束形成并同时抑制干扰.文献[12]介绍了几种通过对主瓣内多个角度进行线性约束达到展宽波束的稳健波束形成,这类方法被称为线性约束最小方差(Linearly Constrained Minimum Variance,LCMV).通过对最优自适应权的构成空间进行分析,我们发现最优权可以通过一个低维的信号加干扰空间进行构造.基于最优权的这一特点,本文提出一种基于稀疏约束的稳健自适应波束形成方法.首先,构造一个完备的信号加干扰空间(IPSS),利用权空间的稀疏特性对组合矢量进行约束,从而达到自适应选择完备IPSS中的最小的一组IPSS来构造自适应权.
2 最优权矢量的空间构成
假设有一N元均匀线阵,存在P个远场窄带干扰.其接收数据可以表示为
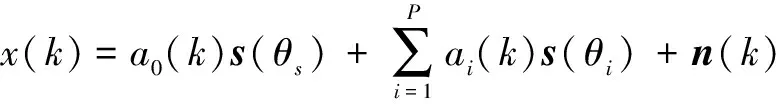
k=1,2,…,L
(1)
其中a0(k),ai(k);i=1,2…P分别表示信号和干扰在k时刻的复幅度,且互不相关;s(θ)表示θ角度的阵列导向矢量;θs和θi分别表示目标和干扰方位角;n(k)为接收噪声,L表示接收样本个数.在最小方差无畸变准则下,自适应权矢量可以写作(不考虑常系数因子)
(2)
其中RI+n为N×N的干扰加噪声协方差矩阵,s(θs)为N×1的目标信号导向矢量(下文中简化为s).一般干扰加噪声协方差矩阵由两部分组成
RI+n=RI+Rn
(3)
其中,分别为干扰协方差矩阵和噪声协方差矩阵,在高斯白噪声情况下Rn=σnI(为单位矩阵),不失一般性,我们假设σn=1.一般情况下,干扰个数小于阵元个数,即P 其中ΛI为P×P的对角矩阵,其对角元素为RI的特征值,UI是由非零特征值对应的特征向量组成的N×P的矩阵.将式(3)代入式(2),并利用矩阵求逆引理[13],可以得到 =[s,UI]c (4) 其中c为(P+1)×1组合矢量 式(4)表明最优自适应权完全位于P+1的期望信号导向矢量加干扰子空间中. 由式(4)可知当噪声为高斯白噪声时,最优权矢量仅由信号导向矢量加干扰空间组成.本节对信号导向矢量和干扰空间分别进行估计.由于干扰数目未知,为了保证权矢量空间的完整性,估计所得的干扰加信号空间必须是完备的.期望信号导向矢量失配是导致传统波束形成性能下降的主要原因之一,因此首先需要对准确的目标导向矢量进行估计.关于信号导向矢量的估计,学者们提出了许多稳健估计方法[7,14,15].本文我们采用文献[7]提出的一种信号导向矢量稳健估计方法. 3.1 估计信号导向矢量 对于传统波束形成方法,当阵列流形精确已知时,目标信号导向矢量是可以直接获得的.但是实际中由于阵列流形误差、来波方向不匹配、信号源的局部散射、阵列校准误差、近场效应等,都会导致信号导向矢量的不匹配.根据文献[15],信号导向矢量估计问题可以转化为一个优化问题,即 (5) 3.2 干扰加信号子空间 (6) (7) 应当注意到对协方差矩阵进行EVD分解构造干扰空间的一种方法,对其进行SVD分解也同样可以实现.另一方面为了避免对协方差矩阵进行估计,实际中还可以直接对数据矩阵X进行SVD分解也可以获得与EVD分解同样的干扰子空间,即 (8) (9) 根据最小方差无畸变准则(MVDR)可以得到 (10) (11) 假设一均匀线阵,阵元个数为N=16,阵元间距为雷达工作波长的一半.真实的期望信号和三个干扰的来波方向分别为2°和-10°,10°,30°,而假设的期望信号来波方向为0°,且三个干扰的干噪比为30dB.为了验证所提算法的有效性,我们将其与对角加载采样协方差求逆方法(LSMI)、特征空间投影法、文献[8]所提的Worst-case 波束形成方法进行比较.其中LSMI的方法[17]的加载量取协方差矩阵最小特征值的10倍,特征空间法所需要的干扰数目是准确已知的,Worst-case 波束形成所需要的误差界为4(导向矢量sHs=N). 实验1 本实验主要讨论平衡因子(正则化参数)λ以及假设的干扰数目K对本文算法的影响.图1所示输出SINR随参数λ的变化曲线,其中信噪比SNR=10dB,所用样本数目为L=100.由图可以看出,本文算法对参数λ具有很好的稳健,λ在很宽的范围内,所提算法的性能都接近最优解. 图2所示为所提算法随所选择的特征向量数目K的变化曲线,其中SNR=10dB,样本数L=100.当K<3算法性能严重下降,当K≥3时,算法性能接近最优值,可以看出所选择的特征向量数目必须大于等于干扰数目,否则算法失效,也从另一个方面验证了所提算法对于IPSS空间完备性的要求. 实验2 本实验主要对所提算法的稳健特性进行仿真验证,并与几种稳健BF进行比较.图3所示为当导向矢量精确已知时,输出SINR与输入SNR变化曲线,其中样本数目L=50.由图可以看出即使期望信号导向矢量精确已知,由于训练样本中含有期望信号,传统的LSMI和Worst-case BF由于信号对消性能而导致性能下降.而本文算法不论在高信噪比还是低信噪比,算法性能都优于传统算法. 图4画出了几种算法性能随样本变化曲线,输入SNR=-10dB,其它参数与图3保持一致.由图可以看出所提算法与其它算法的收敛速度相当,收敛速度大约为干扰数目的2倍. 图5所示为当目标导向矢量存在指向误差时,输出SINR随输入SNR变化曲线,假定的目标方位为2°,真实的目标方位为0°.在低信噪比时,特征空间法性能较差,而对角加载、Worst-case BF和所提算法在低信噪比时,性能相当,所提方法略优于其他两种算法.在高信噪比时,对角加载和Worst-case BF 方法性能严重下降,本文算法略优于特征空间法.图6所示为不同算法的波束方向图,其参数与图5一致,其中SNR=15dB.由图可以看出所提算法波束指向准确,且旁瓣较低,而传统的LSMI方法主瓣角度出现了严重的偏差. 图7所示为期望信号存在局部相关散射情况时的输出SINR随输入SNR变化曲线.此时由于受到局部相关散射的影响,期望信号的导向矢量变为 (12) 其中s(θs)为直达方位的导向矢量;s(θi)表示相关散射路径的导向矢量;θi和φi分别为第i路相关散射的入射角度和相位,且彼此之间相互独立;θi和φi分别服从N(θs,1°)和U(0,2π),N(μ,σ2)表示均值为μ,方差为σ2的正态分布,U(0,2π)表示[0,2π]之间的均匀分布.下述实验中,每一次独立实验中的θi和φi选择都不相同.由图7可以看出,在存在局部相关干扰时,所提算法依然优于其他的算法,且对局部相关信号导致的导向矢量不匹配稳健. 图8所示为受到波前畸变而导致的信号导向矢量失配时,本文算法同其它算法的比较.假设每个阵元对期望信号的波前相位畸变是相互独立的[8],每次独立实验的取值都不相同,但是单次实验中其值保持不变,一般采用高斯随机生成器来产生,其方差为0.01.图8表明本文算法对波前畸变导致的导向矢量不匹配具有很好的稳健性,优于传统算法. 本文通过构造一个低维的完备的干扰加信号子空间,采用构造的完备IPSS空间来线性表示自适应权.首先对信号导向矢量进行稳健估计,其次通过对协方差矩阵进行EVD或者对数据矩阵进行SVD来估计干扰加信号空间.由于干扰个数未知,为了保证IPSS的完备性,构造所得IPSS的维数一般大于等于干扰个数.理论上,最优自适应权仅位于IPSS空间中,为了避免自适应权受到构造的完备IPSS中非干扰加信号部分的影响,本文通过对组合系数进行稀疏约束,自适应的达到从完备IPSS中筛选出维度最小的一组IPSS来表示自适应权,进而达到稳健波束形成的目的.仿真实验表明了所提算法的有效性和稳健性. [1]Gong C,Huang L,Xu D,et al.Knowledge-aided robust adaptive beamforming with small snapshots[J].Electronics Letters,2013,49(20): 1258-1259. [2]杜江,朱柯.智能麦克风阵列语音分离和说话人跟踪技术研究[J].电子学报,2005,33(2): 382-384. Du Jiang,Zhu Ke.Smart micro phone arrays for speech sources separation and speakertracking[J].Acta Electronic Sinica,2005,33(2): 382-384.(in Chinese) [3]Aryafar E,Khojastepour M A,Sundaresan K,et al.ADAM: An adaptive beamforming system for multicasting in wireless LANs[J].IEEE/ACM Transactions on Networking (TON),2013,21(5): 1595-1608. [4]Vorobyov S A.Principles of minimum variance robust adaptive beamforming design [J].Signal Processing,2013,93(12): 3264-3277. [5]陈明建,罗景青.基于双不确定集约束的稳健宽带波束形成算法[J].电子学报,2014,42(3): 587-591. M J Chen,J Q LUO.Robust broadband beamforming algorithm under the double uncertainty set constraints[J].Acta Electronic Sinica,2014,42(3): 587-591.(in Chinese) [6]Olivier B,Stéphanie B.Adaptive processing with signal contaminatedtraining samples[J].IEEE Trans Signal Process,2013,61(17):4318-4329. [7]Gu YJ,Leshem A.Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation[J].IEEE Trans Signal Process,2012,60 (7): 3881-3885. [8]SVorobyov,A Gershman,ZQ Luo.Robust adaptive beamforming using worst-case performance optimization :a solution to the signal mismatch problem[J].IEEE Trans Signal Process,2003,51(2):313-324. [9]Jian L,Petre S,ZSWang.On robust capon beamforming and diagonal loading[J].IEEE Trans on Signal Process,2003,51(7):1702-1715. [10]Dong M,Zheng Q,Su H.Automatic robust adaptive beamforming via ridge regression using l 1-norm approximation[A].2013 International Conference on Radar[C].Adelaide,Australia:IEEE,2013.385-387. [11]C Y Chen,P P Vaidyanathan.Quadratically constrained beamforming robust against direction of arrival mismatch[J].IEEE Trans on Signal Process,2007,55(8):4139-4150. [12]Van Trees H L.Detection,Estimation,and Modulation Theory,Optimum Array Processing[M].New York:John Wiley & Sons,2004.710-887. [13]C D Meyer.Matrix Analysis and Applied Linear Algebra[M].Philadelphia:SIAM,2000.115-124. [14]Hassanien A,Vorobyov S A,Wong K M.Robust adaptive beamforming using sequential quadratic programming: An iterative solution to the mismatch problem [J].IEEE Signal Processing Letters,2008,15:733-736. [15]Khabbazibasmenj A,Vorobyov S A,Hassanien A.Robust adaptive beamforming based on steering vector estimation with as little as possible prior information[J].IEEE Trans on Signal Process,2012,60(6):2974-2978. [16]CVX Research,Inc.CVX: Matlab Software For Disciplined Convex Programming[CP].Version 2.0.http://cvxr.com/cvx,2011. [17]B.D.Carlson.Covariance matrix estimation errors and diagonal loading in adaptive arrays[J].IEEE Trans Aerosp Electron Syst,1988,24(4): 397-401. 解 虎 男,1987年生于陕西渭南,中国空间技术研究院西安分院博士后,研究方向为阵列信号处理和空时自适应信号处理. E-ail:xiehumor@163.com 冯大政 男,1959年生于陕西安康,西安电子科技大学电子工程学院教授,博士生导师.研究方向为雷达信号处理、信号参数估计、仿大脑信息处理、场景感知、模式识别等. A Robust Beamforming Method Based on Sparse Constraint XIE Hu1,2,FENG Da-zheng2,YUAN Ming-dong2 (1.ChinaAcademyofSpaceTechnology,Xi’anBranch,Xi’an,Shaanxi710100,China;2.NationalLaboratoryofRadarSignalProcessing,XidianUniversity,Xi’an,Shaanxi710071,China) By analyzing the constitution of the optimal adaptive weight,we find that the optimal adaptive weight only lies in a low-dimension subspace spanned by the desired signal steering vector and the interferences subspace.Generally,the number of interferences designed to suppress is much smaller than that of the array sensors.Consequently,once the interference-plus-signal subspace (IPSS) is estimated,only a low-dimension combination vector is needed to compute,which leads to a reduction of the computation complexity.First,we construct a complete IPSS.And then the sparse constraint is imposed on the combination vector to select the least number of column vectors of the complete IPSS to form the adaptive weight.Simulation results validate the effectiveness and robustness of the proposed algorithm. robust beamforming;sparse constraint;steering vector mismatch;regularization;convex programming 2014-10-23; 2015-12-30;责任编辑:蓝红杰 国家自然科学基金(No.61271293) TN957 A 0372-2112 (2016)09-2276-06 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.09.0363 构造完备的干扰加信号子空间
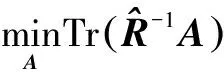
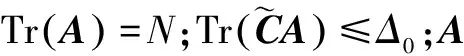
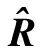
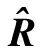
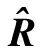
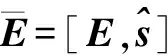

4 基于稀疏表示的波束形成方法
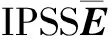
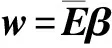
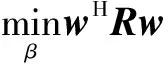
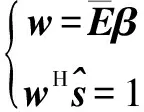
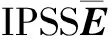
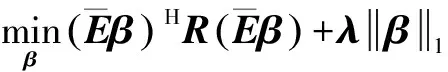
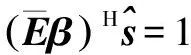
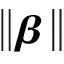
5 计算量分析
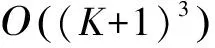
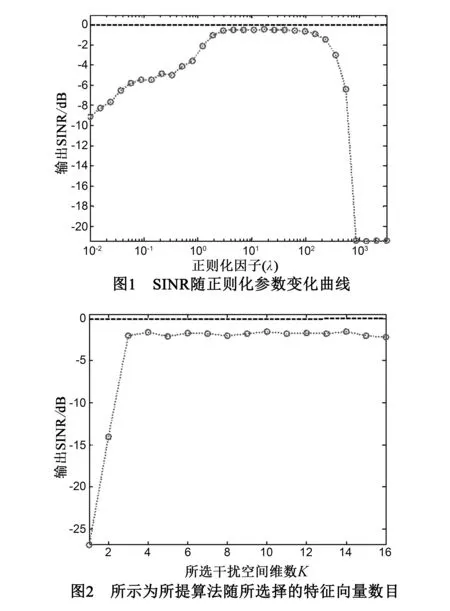
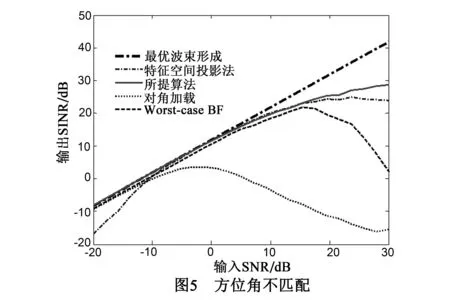
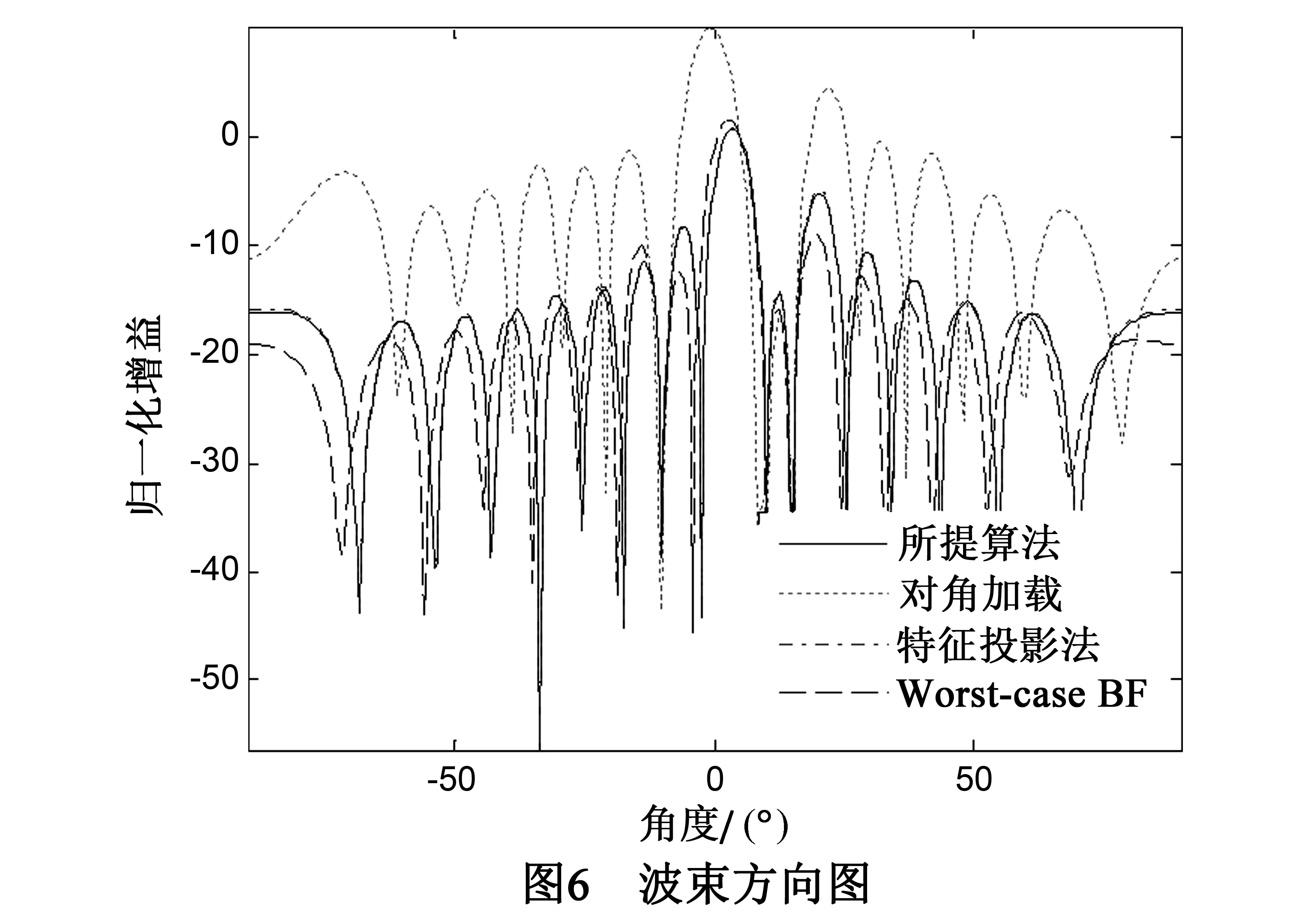
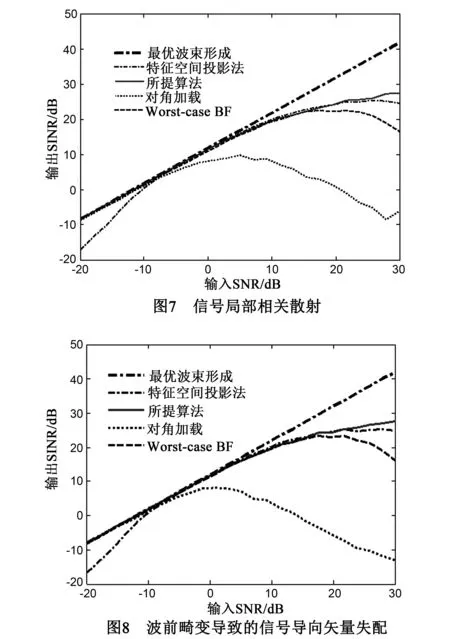
6 实验

7 结论



