基于路径自动分割的测试数据生成方法
廖伟志
(1.嘉兴学院数理与信息工程学院,浙江嘉兴 314001; 2.广西混杂计算与集成电路设计分析重点实验室,广西南宁 530006)
基于路径自动分割的测试数据生成方法
廖伟志1,2
(1.嘉兴学院数理与信息工程学院,浙江嘉兴 314001; 2.广西混杂计算与集成电路设计分析重点实验室,广西南宁 530006)
为了提高路径覆盖测试数据生成效率,研究了路径自动分割方法并结合人工鱼群算法提出了一种路径覆盖测试数据生成方法.首先在分析变量与节点关系、变量与路径关系的基础上提出了路径分割的自动判定及分离算法,实现了变量对子路径有无影响的自动判定;其次引入Levy飞行策略和共轭梯度法对人工鱼群算法进行了改进;然后结合路径分离的结果和改进的人工鱼群算法实现路径覆盖测试数据的生成.在利用人工鱼生成测试数据的过程中,判断是否有人工鱼穿越分离的子路径.如果有,则记录人工鱼中穿越子路径相应的分量并在人工鱼的觅食、聚群及追尾等行为中固定这些分量,从而使得搜索空间不断减少.最后将提出的方法实现程序的测试数据生成,并与相关方法进行了比较.实验结果表明,本文方法在时间开销、成功率及算法稳定性等方面均具有优越性.
软件测试;路径分割;测试数据;路径覆盖;人工鱼群算法
1 引言
软件的可信度是衡量软件质量的一个重要特征,而要提高软件的可信度,软件测试则是一项不可或缺的技术,其重要性是不言而喻的.白盒测试是一种重要的软件测试方法,其中的路径覆盖为白盒测试最重要的测试充分性准则之一.在该准则下,如何有效地生成覆盖路径的测试数据是测试工作的关键.显然,手工生成测试数据是一个非常耗费人力和时间的过程,不仅效率低而且容易出错.为此,需要人们研究有效实现测试数据自动生成的相关理论和方法.至今,人们已经给出多种测试数据自动生成方法,包括随机法、静态法、动态法和试探法[1~3].其中的试探法主要是运用启发式搜索算法实现测试数据的自动生成,已成为国内外研究的热点,如文献[4~7]分别用模拟退火算法、人工免疫算法、禁忌搜索算法及微粒子群优化算法得到满足路径覆盖的测试数据;而文献[8~15]则对遗传算法及元启发式搜索实现路径覆盖测试数据的自动生成进行了研究.人工鱼群算法是李晓磊等模仿鱼类行为方式提出的一种基于动物自治体的优化方法,是集群智能思想的一个具体应用.它能很好地解决非线性函数优化等问题[16].人工鱼群算法是一种有效的寻优算法,具有并行性、简单性、寻优速度较快的特点.实验表明,在诸多领域的应用中人工鱼群算法的性能要优于遗传算法及其它启发式搜索算法.王培崇等[17]用人工鱼群算法实现路径覆盖测试数据的自动生成,实验表明基于人工鱼群算法的测试数据生成效率要高于用粒子群优化方法生成测试数据的效率,也避免了遗传算法存在较易收敛于局部最优的问题.然而,如何把相关技术与人工鱼群算法进行结合以实现路径覆盖测试数据的有效生成有待进一步研究.
上述文献在运用相关算法生成测试数据时,主要是在程序输入的全空间内搜索测试数据.因此,如何缩减搜索空间从而有效提高测试数据的生成效率仍需人们做深入的探讨.文献[18]通过对测试数据的评价提出缩小输入空间的策略,提高算法效率,并将其应用于面向对象的软件测试.张岩等[11]则通过分析目标路径与输入变量之间的关系,将可分目标路径分离出与部分分量相关的子路径;然后固定被穿越子路径对应的输入分量,使种群在不断缩小的空间里寻找测试数据,从而达到提高测试数据生成效率的目的.但路径是否可分的判定及可分路径的分离均是通过人工实现,严重影响测试数据的生成效率.
针对上述问题,本文在研究路径自动分割方法的基础上,结合人工鱼群算法提出了一种路径覆盖测试数据生成方法.首先在分析变量与节点关系、变量与路径关系的基础上提出了路径分割的自动判定及分离算法,实现了路径上哪些输入变量对哪些子路径有影响而对哪些子路径无影响的自动判定.其次,为了提高人工鱼群算法的求解能力,引入Levy飞行策略和共轭梯度法对人工鱼群算法进行了改进.最后结合路径分离的结果和人工鱼群算法实现路径覆盖测试数据的自动生成.在利用人工鱼生成测试数据的过程中,判断是否有人工鱼穿越分离的子路径.如果有,则记录人工鱼中穿越子路径相应的分量并在人工鱼的觅食、聚群及追尾等行为中固定这些分量,使搜索空间不断减少,从而有效地提高了测试数据的生成效率.
2 路径分割的自动判定与分离
张岩等[11]通过分析目标路径与输入变量之间的关系,将可分目标路径分离出与部分分量相关的子路径,但路径是否可分的判定及可分路径的分离均是通过人工实现.本节将在分析变量与节点关系、变量与路径关系的基础上提出一种路径分割的自动判定及分离算法.关于语句块、控制流图及路径等基本概念见文献[11].
2.1 变量与节点的关系
定义1 设x和y分别为被测程序的输入变量,如果在程序中存在赋值语句:y=包含x的表达式,则称变量x显式影响变量y.
定义2 设x,y和z分别为被测程序的输入变量,如果x显式影响y,同时y显式影响z,则称x隐式影响z.
把x显式影响y或x隐式影响y统称为x影响y.
定义3 设x和P分别为被测程序的输入变量及控制流图的路径,n为路径P上的一个节点,若n为决策节点且x出现在该节点中,或者x出现在非决策节点n的赋值语句中,则称变量x显式影响节点n.
定义4 设x,y为被测程序的输入变量,n为路径P上的一个节点,若x显式影响节点n而且y影响x,则称变量y隐式影响节点n.
把变量x显式影响节点n或变量x隐式影响节点n统称为变量x影响节点n.
为了描述变量对变量的影响及变量对节点的影响,本文定义两个矩阵:一个是路径P上变量对变量影响的矩阵A,另一个则是变量对路径P上各个节点影响的矩阵B.设路径P={s,n1,…,nk,e}上的输入变量集X={x1,…,xm},用m×m矩阵表示变量对变量影响的矩阵,且规定矩阵第i行第j列的元素
用m×k矩阵表示变量对路径P上各个节点影响的矩阵,且规定矩阵第i行第j列的元素

矩阵A的求解步骤如下:①首先置矩阵A的初始值为0;②扫描路径P上的各个非决策节点,如果节点中含有赋值语句{xj=包含xi的表达式},则令aij的值为1;③如果aij=1且ajt=1,则令ait的值为1;④反复执行③直到矩阵A元素值不再发生改变.
矩阵B的求解步骤如下:①首先置矩阵B的初始值为0;②扫描路径P上的各个节点;如果xi显式影响节点nj,则令bij的值为1;③如果aij=1且bjt=1,则令bit的值为1;④反复执行③直到矩阵B元素值不再发生改变.
2.2 变量与路径的关系
定义5 设B为变量对路径P上各个节点影响的矩阵,如果矩阵的第i行元素满足:存在j(1≤j≤k)使得对任何大于等于1且小于等于j的整数l均有bil=0,则称节点nj和nj+1(j+1≤k)为基于变量xi在路径P上的分界点,且称变量xi不影响P的子路径{n1,…,nj}.
定义6 设B为变量对路径P上各个节点影响的矩阵,如果矩阵的第i行元素满足:存在j(1≤j≤k)使得对任何大于等于j且小于等于k的整数l均有bil=0,则称节点nj和nj-1(1≤j-1)为基于变量xi在路径P上的分界点,且称变量xi不影响P的子路径{nj,…,nk}.
定义7 设变量集V={x1,…,xm}且路径P上的节点分别为n1,…,nk(不含起始和结束节点),如果存在节点nj(1≤j≤k)使得该节点为V中任意变量在路径P上的一个分界点,则称该路径基于变量集V是可分的.
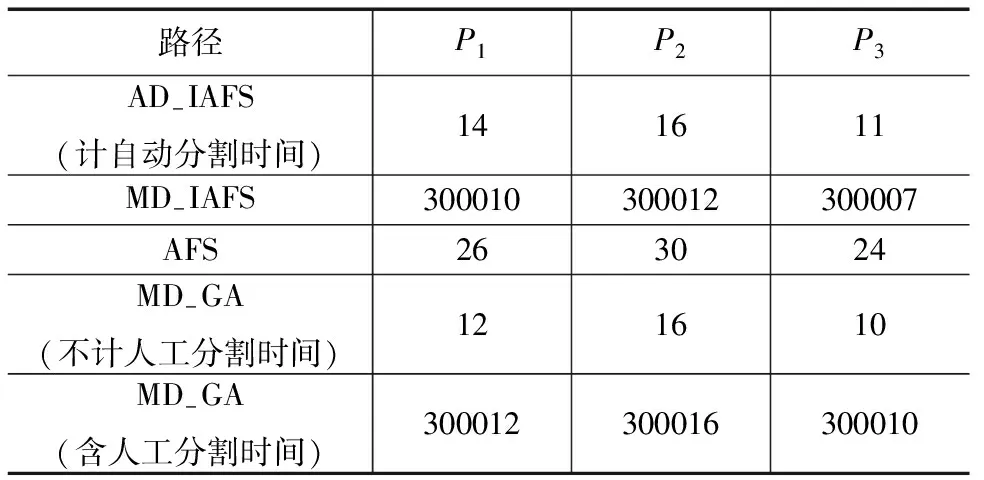
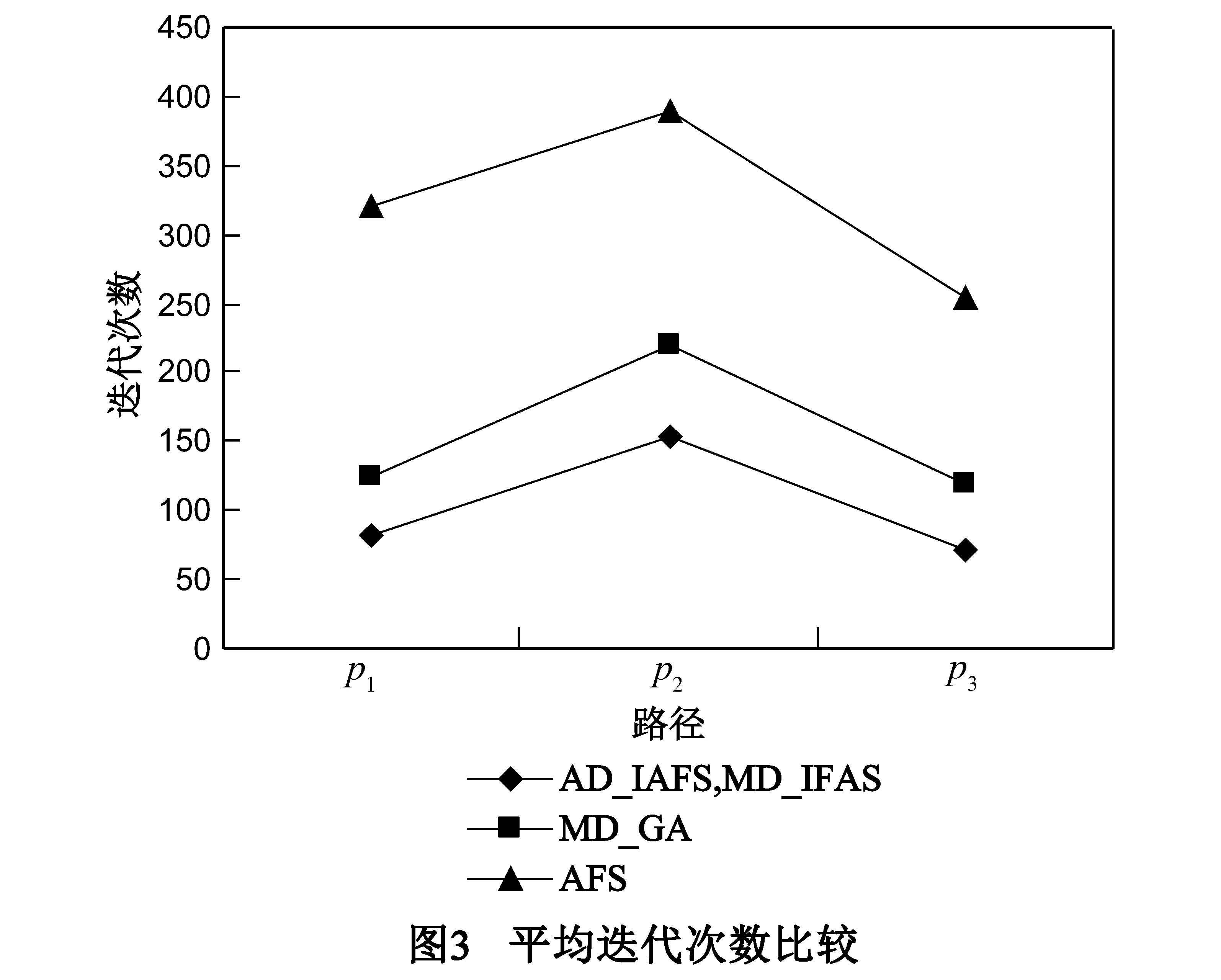
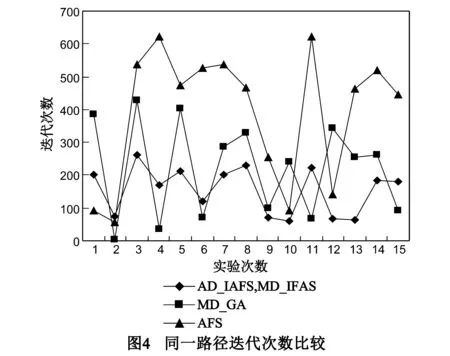
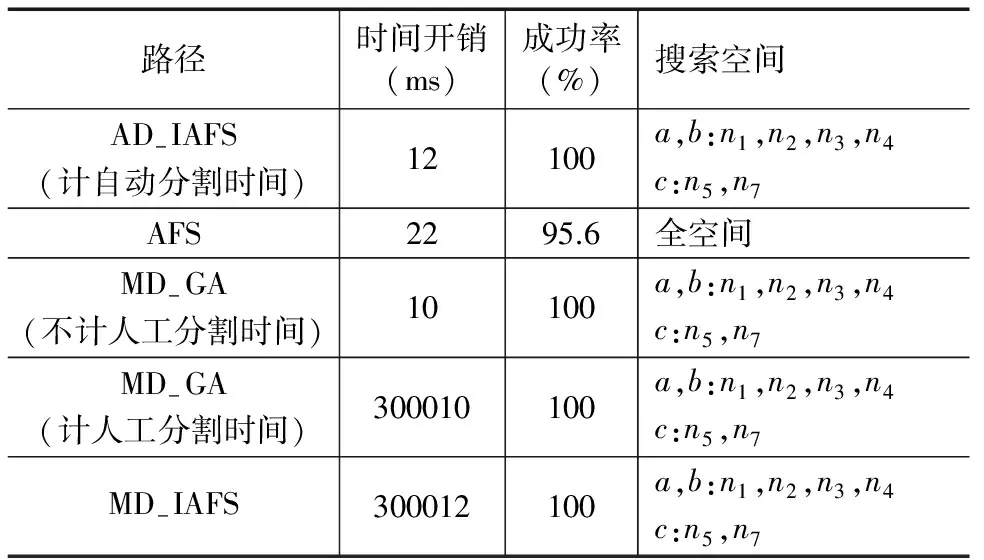
性质1 设节点nj为可分路径P={n1,…,nk}上的分界点,则有:①如果j=1,则路径分割为{n1}和{n2,…,nk}两部分;②如果j=k,则路径分割为{nk}和{n1,…,nk-1}两部分;③如果1 定理1 设节点nj为可分路径P={n1,…,nk}上的分界点且把P分割为{n1,…,nj}和{nj+1,…,nk}两条子路径,若V为P上的变量集,则基于该分界点V可分为两个变量子集V1和V2,且同一变量子集中的每个变量不影响而且仅不影响P的同一条子路径. 证明 由于路径P基于变量集V是可分的且分界点为nj,根据定义7易知节点nj均为V中任意变量在路径P上的一个分界点,因此由定义5,6可知V中任意变量必然不影响P的子路径{n1,…,nj}或者不影响子路径{nj+1,…,nk},不妨把那些不影响{n1,…,nj}的变量放在变量子集V1,而把那些不影响{nj+1,…,nk}的变量放在变量子集V2,显然有V1∩V2=(且V1∪V2=V,证毕. 2.3 路径分割的自动判定及分离算法 设路径P基于变量集V是可分的且有l种路径分割方法,那么哪一种分割是最好的?由于变量不影响路径的长度越长则测试数据的搜索空间就会越小,因此若各个变量不影响路径的长度总和越大,则总的测试数据搜索空间就越小.为此本文选择使得变量不影响路径的长度总和最大的分割方法为最好的分割方法.设某种分割法的分界点为nj,基于该分界点V可分为两个变量子集V1和V2,且V1不影响{n1,…,nj}而V2不影响{nj+1,…,nk},则V中所有变量不影响路径的总长度计算方法如下式: length=|V1|×j+|V2|×(k-j) (1) 其中|V1|和|V2|分别为集合V1和V2的元素个数. 下面给出路径分割的自动判定及分离算法,主要思想如下:首先扫描路径上各个节点的变量;然后构造变量对变量影响矩阵A及变量对节点影响矩阵B;其次由矩阵B找出基于各个变量在路径上的分界点集,然后依据分界点集的交集判定路径是否可分,若可分则根据式(1)确定分割方案;最后输出分割的路径及对应的变量子集.具体的实现步骤见算法1. 算法1 路径分割的自动判定及分离算法 输入:控制流图的路径P 输出:路径分割信息 (3)科技英语利用隐喻转移语义,具体表现如下:一是把熟知事物的性质转移到另一事物。例如connecting rod(连杆),intake valve(进气门)等。 二是把熟知事物的形状转移到新事物上,如I-steel beam(工字钢梁),pincer pliers(老虎钳)等。三是将熟知事物结构转移给新事物,如body(车身),exhaust valve(排气阀)等。四是把原有领域的术语用于另一领域,产生新的词义,如 hollow(洞)--凹槽、jacket(夹克)--套等。 步骤: Step 1 扫描路径P上各个节点的变量并置入变量集V中. Step 2 构造矩阵A. Step 3 构造矩阵B. Step 4 根据矩阵B确定基于各个变量xi在路径P上的分界点集Si. Step 5 令Scom=Si1∩Si2∩…∩Sil,其中l=|V|. Step 6 若Scom为空集,则表明路径P不可分,转至Step 8. Step 7 若Scom不为空集,则依据式(1)查找使length为最大的分割法并输出分割的路径及变量子集V1和V2. 3.1 主要思想 对于给定的路径P,在人工鱼群算法中按如下形式定义人工鱼:人工鱼的每个分量对应于目标路径上的一个变量.根据设计的评价函数,利用人工鱼群算法中的觅食、聚群及追尾等行为改变人工鱼的位置(即改变输入变量的值)从而得到所需的路径覆盖测试数据.在此过程中,首先根据算法1对目标路径进行分离,然后确定不影响各个子路径的变量集,接着判断是否有人工鱼穿越分离的子路径.如果有,则记录该人工鱼中穿越子路径相应的分量,并在人工鱼前进的过程中固定这些分量的值,即不再去搜索这些分量的域空间,因此测试数据的搜索空间将不断得到缩小从而能够有效地提高测试数据的生成效率. 3.2 初始鱼群的构造 设目标路径P上的m个变量及其取值范围分别为a1∈[min1,max1],…,am∈[minm,maxm],人工鱼X包含m个分量x1,…,xm,分别对应于变量a1,…,am,初始人工鱼第i个分量xi的值为[mini,maxi]中的一个随机值. 3.3 评价函数的设置 人工鱼X包含|V|个分量(其中V为目标路径P上的变量集合),每个分量对应于V中的一个变量,第i个分量记为xi.记path(X)为X穿越的路径,穿越目标路径P的输入为X*,若X与X*相同,则X就是所求的测试数据. 人工鱼X穿越的路径path(X)与目标路径P的距离如下式: dis(path(X),P)=lev(path(X),P)+bra(path(X),P) (2) 其中lev(path(X),P)为path(X)与P的层距离,而bra(path(X),P)为path(X)与P的分支距离,关于这两个距离的计算方法见文献[19]. 设人工鱼X优劣的评价函数为f(X),其定义见式(3): f(X)=dis(path(X),P) (3) f(X)越小的人工鱼就意味着该人工鱼越优,当f(X)=0时,该人工鱼就是所求的解. 3.4 人工鱼行为 在觅食行为中,如果当前人工鱼X的第i个分量xi就是穿越了可分离目标路径P的某一子路径的数据,则该分量的值就被固化,即随机状态Y的第i个分量的数据就等于xi,只需改变X中不满足此类条件的分量.觅食行为中随机状态Y的各分量值由式(4)给出: (4) 在聚群行为中,如果当前人工鱼X的第i个分量xi或者X伙伴的第i个分量zi就是穿越了可分离目标路径P的某一子路径的数据,则中心位置Yc第i个分量的数据就等于xi或zi,否则等于X所有伙伴在该分量的数据和的平均值.中心位置Yc各分量的值按式(5)计算: (5) 其中nf为当前人工鱼X领域内的伙伴数目,zi为X某个伙伴的第i个分量.其它人工鱼行为同基本人工鱼群算法. 3.5 人工鱼群算法的改进 人工鱼群算法作为一种随机搜索算法,具有对初值要求不高、全局收敛性好、鲁棒性强、简单易实现的优点,但人工鱼群算法尤其是基本人工鱼群算法也存在着寻优精度不高、后期收敛速度慢的问题.为了解决这些问题,人们已经在诸多方面对算法进行改进,主要改进的策略有:①自适应调整视野和步长,提高了收敛速度和寻优精度;②引入禁忌表避免位置的重复访问从而增强全局寻优能力和寻优效率;③为防止人工鱼在游动中出现退化采取了最优个体保留策略,该策略使得算法具有求解精度高、寻优成功率高、收敛速度快及算法稳定等优点. 本文人工鱼群算法除了采取上述的改进方法之外,还提出了如下的改进策略: (1)利用Levy飞行使人工鱼跳出局部极值 Levy飞行会产生较大跳跃从而能够有效跳出局部极值,已有的人工鱼群算法还没有采用Levy飞行来解决人工鱼跳出局部解的问题.本文采用Levy飞行模式来模拟人工鱼的跳跃行为,使得人工鱼在游动过程中能够有效跳出局部极值.人工鱼位置的更新公式如下: Xj+1=Xj+α⊕Levy(λ) (6) (2)采用共轭梯度法提高人工鱼的局部寻优能力 在人工鱼群算法中引入共轭梯度法的目的在于:与基本人工鱼群算法不同,经过更新后的人工鱼位置不是直接进入下一次迭代,而是把得到的人工鱼位置的梯度和共轭因子相乘后加到负梯度上计算出一组共轭方向,然后沿该方向搜索得到人工鱼的新位置,之后再进入下一次迭代,从而保证了算法的局部寻优能力得到提高.在本文人工鱼群算法中共轭梯度法的主要步骤如下: 3.6 算法流程 算法2 路径覆盖测试数据生成算法 输入:程序控制流图的路径P 输出:覆盖路径P的测试数据 步骤: Step 1 设置人工鱼群的相关参数、初始化种群、输入目标路径P的相关信息. Step 2 调用算法1并插桩被测程序. Step 3 根据评价函数计算各人工鱼的适应值,将该适应值与公告板的最优人工鱼进行比较,若更优则将其赋给公告板.同时,在禁忌表中记录各条人工鱼已达到的历史最优点及已遍历的解空间. Step 4 根据如下公式[20]自适应计算人工鱼的视野与步长: Step 5 判断是否有人工鱼穿越由P分离出的子路径.如果有,则记录影响该子路径变量的值,用该值替换其它人工鱼相应分量的值并固化. Step 6 若已经迭代M次人工鱼的适应值未有明显变化,则利用Levy飞行使人工鱼跳出局部极值;否则根据觅食行为、聚群行为和追尾行为并结合最优个体保留策略计算人工鱼新的位置. Step 7 采用共轭梯度法计算人工鱼的新位置. Step 8 若满足终止条件则输出最优解,算法结束,否则转至Step 9. Step 9 若新位置在禁忌表中,则转至Step 4,否则转至Step 3. 为了对本文所提出的方法提供技术支持,在Windows操作系统下采用C++语言开发了两个程序,包括C程序路径的自动分割程序(Automatic Division of Path,简称ADP)和用于生成测试数据的人工鱼群算法(Artificial Fish Swarm Algorithm for Test Data Generation,简称AFS-TDG).在ADP的设计中,首先利用编译技术实现了C程序路径上各个节点所包含变量的识别,然后根据算法1进行代码设计与实现,最后输出分割的路径及其相关的变量子集.而AFS-TDG则是在已有的基本人工鱼群算法的程序代码基础上增加了实现禁忌表的读写、人工鱼视野与步长的自适应调整、利用Levy飞行使人工鱼跳出局部极值、最优个体保留及共轭梯度法调整人工鱼位置等功能的代码. 为了验证本文方法的有效性,选择文献[11]中图3所示的sumday程序作为基准程序.将本文方法与文献[11]及文献[17]所提出的方法进行比较.为了便于叙述,把本文的方法称为自动分割-改进人工鱼方法(简称AD-IAFS方法),同时考察人工分割-改进人工鱼方法(简称MD-IAFS方法).文献[11]所提出的方法称为人工分割-遗传方法(简称MD-GA方法)而文献[17]的方法称为人工鱼方法(简称AFS方法).实验硬件环境为2.8GHz PC机、2GB内存;软件环境为WinXP+Visual C++6.0.在本文的试验中,对于MD-GA方法生成测试数据时所采用的相关参数不做任何改变,仍采用文献[11]所采用的参数:交叉概率为0.9,变异概率为0.3,输入变量的范围为[0,2047],种群规模为50而最大进化代数为2000.AD-IAFS和MD-IAFS方法中主要参数设置如下:视野和步长分别为120和18,鱼群规模为20,λ=1.7,M=10.类似于AD-IAFS,在AFS中人工鱼视野和步长也分别为120和18,鱼群规模为20. 考虑sumday程序控制流图的3条路径:P1={s,n1,n3,n5,n6,n5,n6,n5,n7,e},P2={s,n1,n2,n3,n5,n6,n5,n7,e},P3={s,n1,n2,n3,n5,n6,n5,n6,n5,n6,n5,n6,n5,n6,n5,n6,n5,n6,n5,n6,n5,n6,n5,n7,e}.P1可分割为路径P11={n1,n3}和P12={n3,n5,n6,n5,n6,n5,n7},其中变量year只影响P11而不影响P12,而变量month和day只影响P12而不影响P11.P2可分割为路径P21={n1,n3}和P22={n3,n5,n6,n5,n7},其中变量year只影响P21而不影响P22,而变量month和day只影响P22而不影响P21.P3可分割为路径P31={n1,n3}和P32={n3,n5,n6,n5,n6,n5,n6,n5,n6,n5,n6,n5,n6,n5,n6,n5,n6,n5,n6,n5,n7},其中变量year只影响P31而不影响P32,而变量month和day只影响P32而不影响P31. 对于所要比较的四种方法,每种方法均进行15次实验.图3显示了AD-IAFS、MD-IAFS、MD-GA和AFS方法生成覆盖路径P1、P2和P3测试数据所需要的平均迭代次数,对于每条路径AD-IAFS方法和MD-IAFS所需的迭代次数均是最少的,说明了本文具有路径分割的改进人工鱼群算法均优于AFS算法和有路径分割的遗传算法.由表1可知,AD-IAFS方法的时间开销比AFS方法平均要少一半而与不计人工分割路径的MD-GA方法时间开销相当,但远远小于含人工分割路径时间开销的MD-GA方法和MD-IAFS方法.需要说明的是,在本实验中,P1、P2和P3路径人工分割的平均时间开销为5分钟,即为300000毫秒.如果程序的控制流图规模增加,人工分割路径的平均时间开销远不只5分钟.由此可以看出,基于路径分割的搜索空间缩减方法能够有效地提高测试数据的生成效率,但其前提是:路径的分割一定是由计算机自动完成,否则依靠人工分割路径并不能真正提高效率,反而其时间开销都远大于任何一种已有测试数据生成方法的时间开销.由表2可知,基于路径分割的AD-IAFS、MD-IAFS和MD-GA方法生成测试数据的成功率均能达到100%,而AFS方法生成穿越路径P1、P2和P3的测试数据成功率分别为92.5%,98.7%和97.2%.由以上数据不难看出,AD-IAFS方法生成测试数据的效率均明显高于MD-GA、MD-IAFS和AFS方法,其成功率和MD-GA、MD-IAFS方法相当而高于AFS方法.从路径搜索空间对比表3可看出,在基于路径分割的测试数据生成方法中,在穿越n1,n3时只对year进行搜索,而不对month和day进行搜索;而在穿越n3,n5,n6,n7时只对month和day进行搜索,而不对year进行搜索.不采用基于路径分割的AFS则需要进行全空间搜索. 表1 时间开销 表2 成功率 表3 路径P1搜索空间对比 图4给出了三种方法在同一路径P2上15次实验的迭代次数.从图中的数据可以看出,由于三种方法每次实验的初始种群都是随机产生,因此每次生成测试数据的迭代次数都有变化.其中AFS方法迭代次数变化大,在图中可以看出反映AFS变化的折线跳跃幅度最大,其次是MD-GA方法,而反映AD-IAFS和MD-IAFS变化的折线跳跃幅度最小.事实上,MD-GA方法迭代次数的方差值为19879.5,AFS方法迭代次数的方差值为38437.2,而AD-IAFS和MD-IAFS方法的方差值为4743.1,该值为MD-GA方法的1/4而仅为AFS方法的1/8左右,说明本文方法的稳定性均比MD-GA和AFS方法好. 再考察上述几种方法在如图1程序测试数据生成效率的对比情况.表4给出了如图1程序路径P测试数据生成在时间开销、成功率及搜索空间的比较.表中的数据显示,AD-IAFS方法在时间开销(含路径分割时间)最少,成功率是100%,搜索空间和其它基于路径分割的测试数据生成方法相当.综合这些指标,本文提出的AD-IAFS方法仍为最好的方法,与在上述sumday程序测试的结论是一致的. 表4 如图1程序路径P测试数据生成对比 从实验数据不难看出,基于计算机实现的路径自动分割方法相比人工路径分割方法在时间效率上优势明显.另一方面,人工分割不仅需要测试人员掌握分割方法,而且在分割的过程中容易出错,分割的正确性难以保证,因此可靠性差;而自动分割方法由于是通过计算机实现,速度快而且可靠性高. 本文提出一种新的路径覆盖测试数据生成方法,主要贡献包括:①提出一种路径分割自动判定与分离方法,解决了人工分割路径的弊端,为在测试数据生成过程中缩减搜索空间以提高生成效率提供了一种有效的方法;②给出了基于Levy飞行和共轭梯度的人工鱼群改进算法,改进的人工鱼群算法不仅能有效提高局部寻优能力而且能有效避免人工鱼陷入局部最优;③提出了基于路径分割的测试数据生成人工鱼群算法.实验表明该方法是一种有效的测试数据生成方法,在时间开销、成功率及算法稳定性方面均具有优越性. 当前主要将所提出的方法用于单路径覆盖测试数据的生成.如何把本文的方法运用到多路径覆盖测试数据的生成从而满足实际应用中复杂软件多路径覆盖测试数据生成的需求仍需做进一步研究. [1]巩敦卫,张婉秋.基于自适应分组的大规模路径覆盖测试数据进化生成[J].控制与决策,2011,26(7):979-983. Gong Dunwei,Zhang Wanqiu.Evolutionary generation of test data for many paths coverage based on adaptive grouping[J].Control and Decision,2011,26(7):979-983.(in Chinese) [2]张婉秋.基于遗传算法的多路径覆盖测试数据生成方法[D].江苏徐州:中国矿业大学,2010. Zhang Wanqiu.Genetic algorithm based test data generation for multiple paths coverage[D].Xuzhou,Jiangsu:China University of Mining and Technology,2010.(in Chinese) [3]Stefan J Galler,Bernhard K Aichernig.Survey on test data generation tools[J].International Journal on Software Tools for Technology Transfer,2014,16(6):727-751. [4]Nigel Tracey,John Clark,Keith Mander.An automated framework for structural test-data generation[A].Proceedings of the International Conference on Automated Software Engineering[C].USA:IEEE,1998.285-285. [5]Xiaofeng Xu,Yan Chen,Xiaochao Li.A path-oriented test data generation approach for automatic software testing[A].Proceedings of the 2ndInternational Conference on Anti-counterfeiting,Security and Identification[C].Piscataway:IEEE,2008.63-66. [6]Eugenia Diaz,Javier Tuya,Raquel Blanco.A tabu search algorithm for structural software testing[J].Computers & Operations Research,2008,35(10):3052-3072. [7]胡岳峰,高建华.一种面向对象测试用例自动生成的混合算法[J].计算机应用研究,2008,25(3):786-788. Hu Yuefeng,Gao Jianhua.Hybrid algorithm of automatically generating of test data for object-oriented program[J].Application Research of Computers,2008,25(3):786-788.(in Chinese) [8]Moataz A Ahmed,Irman Hermadi.GA-based multiple paths test data generator[J].Computers & Operations Research,2008,35(10):3107-3124. [9]Paulo Marcos Siqueira Bueno,Mario Jino.Automatic test data generation for program paths using genetic algorithms[J].International Journal of Software Engineering and Knowledge Engineering,2002,12(6):691-709. [10]Jin-Cherng Lin,Pu-Lin Yeh.Automatic data generation for path testing using Gas[J].Information Sciences,2001,131(1-4):47-64. [11]张岩,巩敦卫.基于搜索空间自动缩减的路径覆盖测试数据进化生成[J].电子学报,2012,40(5):1011-1016. Zhang Yan,Gong Dunwei.Evolutionary generation of test data for path coverage based on automatic reduction of search space[J].Acta Electronica Sinica,2012,40(5):1011-1016.(in Chinese) [12]A A Sofokleous,A S Andreou.Automatic evolutionary test data generation for dynamic software testing[J].Journal of System and Software,2008,81(11):1883-1898. [13]谢晓园,徐宝文,史亮,聂长海.面向路径覆盖的演化测试用例生成技术[J].软件学报,2009,20(12):3117-3136. Xie Xiaoyuan,Xu Baowen,Shi Liang,Nie Changhai.Genetic test case generation for path-oriented testing[J].Journal of Software,2009,20(12):3117-3136.(in Chinese) [14]Yong Chen,Yong Zhong.Automatic path-oriented test data generation using a multi-population genetic algorithm[A].Proceeding of the 4th International Conference on Natural Computation[C].Piscataway:IEEE Press,2008.565-570. [15]Chengying Mao.Structural test data generation based on harmony search[J].Lecture Notes in Computer Science,2013.353-360. [16]李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践,2002,22(11):32-38 Li Xiaolei,Shao Zhijiang,Qian Jixin.An optimizing method based on autonomous animats:fish-swarm algorithm[J].Systems Engineering-Theory & Practice,2002,22(11):32-38.(in Chinese) [17]王培崇,钱旭.基于改进鱼群算法的路径测试数据生成[J].计算机应用,2013,33(4):1139-1141. Wang Peichong,Qian Xu.Path test data generation based on improved artificial fish swarm algorithm[J].Journal of Computer Applications,2013,33(4):1139-1141.(in Chinese) [18]JCB Ribeiro,MA Zenha-Rela,FFD Vega.Test case evolution and input domain reduction strategies for the evolutionary testing of object-oriented software[J].Information and Software Technology,2009,51(11):1534-1548. [19]McMinn P.Evolutionary Search for test data in the presence of state behavior[D].Sheffied,England:University of Sheffied,2005. [20]王联国,洪毅.基于冯·诺依曼领域结构的人工鱼群算法[J].控制理论与应用,2010,27(6):775-780. Wang Lianguo,Hong Yi.Artificial fish-swarm algorithm based on Von Neuman neighborhood[J].Control Theory & Applications,2010,27(6):775-780.(in Chinese) 廖伟志 男,1974年生于广西凤山,教授,博士,主要研究方向:软件测试、智能计算. E-mail:weizhiliao2002@aliyun.com Test Data Generation Based on Automatic Division of Path LIAO Wei-zhi1,2 (1.CollegeofMathematicsPhysicsandInformationEngineering,JiaxingUniversity,Jiaxing,Zhejiang314001,China;2.GuangxiKeylaboratoryofHybridComputationandICDesignAnalysis,Nanning,Guangxi530006,China) In order to improve the efficiency of test data generation for path coverage,a method for generating test data was proposed,which was based on automatic division of path and artificial fish-swarm (AFS) algorithm.Firstly,the relations between variables and nodes,and between variables and paths,were analyzed.Based on the analysis an algorithm for automatic division of path was presented,which can automatically judge the impact of variables on sub-paths.Secondly,an improved AFS algorithm was developed based on Levy flying and conjugate gradient.By making use of the result of path division and the improved AFS algorithm,a new method for searching test data was proposed.If there exist sub paths that the fish pass through in the process of using AFS to generate test data,the corresponding component of these fish were fixed,so that search space were reduced.Finally,the proposed method was applied to the test data generation of programs.It is shown that our method outperforms the related methods in running time,success rate and stability. software testing;path division;test data;path coverage;artificial fish-swarm algorithm 2014-10-10; 2015-03-26;责任编辑:蓝红杰 国家自然科学基金(No.61163012);广西高校科研资助项目(No.2013ZD040);广西混杂计算与集成电路设计分析重点实验室开放基金课题(No.2012HCIC01) TP301 A 0372-2112 (2016)09-2254-08 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.09.034
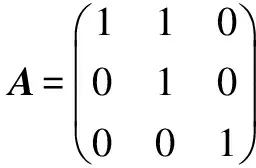
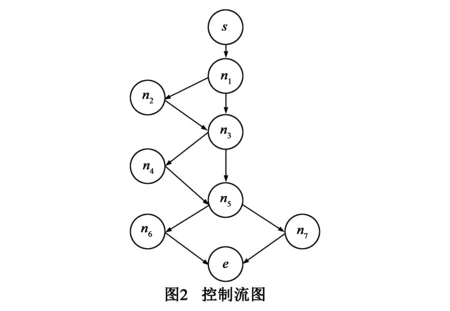
3 基于路径分割和人工鱼群算法的测试数据生成

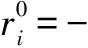

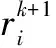
4 实验


5 结论


