一种基于链路质量的自维护拓扑控制博弈算法
陈 白,辛敏洁,刘伟静,姚 宁,郝晓辰,汝小月
(燕山大学电气工程学院,河北秦皇岛 066004)
一种基于链路质量的自维护拓扑控制博弈算法
陈 白,辛敏洁,刘伟静,姚 宁,郝晓辰,汝小月
(燕山大学电气工程学院,河北秦皇岛 066004)
针对无线传感器网络拓扑性能优化单一的问题,本文首先定义了表征双向通信质量的指标.其后将链路质量,节点干扰,剩余能量均衡性等参数融入收益函数,设计了一种基于链路质量的自维护拓扑控制博弈算法SMGLQ.理论证明该算法能保证各节点收敛到帕累托最优.仿真实验表明它能为网络选择通信质量较好的链路,并降低能耗.
无线传感器网络;拓扑控制;链路质量;博弈论
1 引言
无线传感器网络(Wireless Sensor Network,WSN)是一种多跳的自组织无线通信网络.拓扑结构是WSN的支撑构架,有着非常重要的作用.由于节点的能量有限,目前对拓扑控制算法的研究主要集中于如何延长网络生命期.然而随着WSN日益广泛的应用,仅延长网络生命期已经不能满足使用需求.因此,如何在延长网络生命期时兼顾网络其他性能对拓扑控制具有重要意义.
拓扑性能相互独立又相互影响,针对这一特点,博弈论被用来优化网络性能.文献[1]引入虚拟博弈完成算法构建过程,进一步降低了博弈过程中信息交互的能耗.Cho等人设计的算法能兼顾网络能耗与覆盖率[2],然而,在能耗较低时网络覆盖性较差.文献[3]以节能与降低干扰为目的,使用信干噪比构造收益函数;Miao等人致力于能耗与网络延时的协同优化[4],需要注意的是,网络延时和干扰并不仅仅与拓扑性能相关.这些算法重点提高了拓扑某一方面的性能,其余性能的优化只是作为附加效果,并不能对拓扑的性能做出整体性提高.文献[5]中提出的EBRGA算法融合了各层信息构建博弈模型,对网络性能做出较全面的优化,但在构建拓扑时并没有考虑网络中链路的通信质量.文献[6]分析并证明了数据传输正确率对网络性能的重要性,因此需要通过选择通信质量较好的链路以增加数据传输正确率.XTC算法仅仅定性地使用路径长度来度量链路通信质量.其后,节点间最小可达功率[7],期望传输数ETX[8]也被用作链路质量的评价标准.这些指标从侧面反映了当前链路的通信质量,并不能体现出通信情况的动态变化.接收信号强度指标(Received Signal Strength Indicator,RSSI)能反映当前通信链路的信噪比,因此许多算法将其作为链路通信质量的评价标准[9].然而RSSI并不能准确表示当前的链路质量,因此需要更全面精准的度量标准来衡量链路通信质量.
针对上述情况,本文将多种性能参数融入收益函数,设计了一种基于链路质量的自维护拓扑控制博弈算法SMGLQ.理论分析证明该算法能保证网络连通并且网络中所有节点均能达到帕累托最优纳什均衡状态.仿真结果表明SMGLQ算法所构建的拓扑不仅具有良好的鲁棒性和稀疏性,还能有效延长网络生命期.
2 链路通信质量评价指标
目前链路质量评价指标中最常用的有三种:收包率PRR,链路质量指标LQI,信号接收强度指标RSSI.其中,PRR最能明确反映链路通信质量,然而,由于它是统计量,无法直接通过硬件测得.与PRR不同,RSSI和LQI均可通过硬件实时测得.与RSSI相比,LQI能更加准确地描述链路通信质量,但是LQI并不能及时将通信的变化反映到自身数值上.RSSI虽然能随着通信环境的变动而变化,但是其数值并不能精准地表示当前环境下的通信质量.由此可知,单一的使用LQI或者RSSI表示链路通信质量是不全面的,应考虑综合LQI的准确性与RSSI的灵敏性来衡量链路通信质量.
在实际通信中,低功耗无线模块的通信模式通常具有不规则性,尤其是节点进行地面通信时,这个问题会更加显著.链路的不对称性体现在,当节点对进行相互通信时,正反向的链路质量不一致,因此导致正反向的收包率不一致.不对称链路会引发一系列问题,比如在网络层,不能正常建立路由树;在MAC层,不能通过确认消息进行冲突避免等.鉴于此类原因,应在拓扑构建过程中考虑链路的不对称性,用正反两向的链路质量指标综合地表示该链路的通信质量.网络中任意节点对i,j之间进行通信时,j每次接收到i发送的数据后直接读取相应的RSSI(i,j)和LQI(i,j),其后求出链路ij的通信质量CQ (Communication Quality)
(1)
当i,j进行相互通信时,链路ij的双向通信质量可表示为
Bi-CQ(ij)=CQ(i,j)×CQ(j,i)
(2)
其中,RSSI(i,j)∈[RSSImin,0],LQI(i,j)∈[0,LQImax].λ,η表示其对应部分在评价指标CQ中所占的比例,说明了链路质量指标与信号接收强度指标对CQ的影响.使用相同发射功率时,RSSI(i,j)和LQI(i,j)的值越大,表明当前的链路通信状况越好.
3 博弈模型建立
3.1 基于链路质量的拓扑控制博弈模型
拓扑性能相互独立又相互影响,而博弈论能很好的处理相互决策过程中的最优化问题.因此本文使用博弈实现多种性能协同优化的目标.基本的博弈三要素记为G={I,s,u},具体说明为:
(1)参与者集合I.所有传感器节点作为博弈的参与者I可表示为I={1,2,…,N}.其中N是参与者的数量.
(2)策略空间s.策略集合s={s1,s2,…,sN}为其策略空间.其中si=(pi)为节点i的策略空间,pi∈P,P为节点的可选功率集合.
(3)收益函数u.本文从以下方面来设计任意节点i的收益函数ui.
①网络连通性.对于任意拓扑而言,连通性都是必须满足的首要性能.定义网络连通因子为fi(pi,p-i).当网络连通时fi(pi,p-i)=1,反之fi(pi,p-i)=0.显然,对于网络中任意节点i∈I,且发射功率满足pi>qi时,fi(pi,p-i)≥fi(qi,p-i).
②节点发射功率.传感器节点能量有限并且补给困难,因此,需要为剩余能量较低的节点分配较小的功率以延长节点生存时间.定义功率与节点剩余能量间的关系为pe(pi)=pi/Ei.其中,pi是节点i当前发射功率,Ei为当前剩余能量.
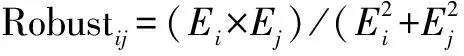
④剩余能量均衡性.当网络中节点剩余能量分布不均衡时,能量较小的节点会较早死亡,从而对网络性能造成影响.节点i单跳范围内所有邻居的剩余能量方差可表示i的剩余能量均衡性
(3)
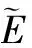
⑤节点度.节点度能影响网络的鲁棒性、稀疏性等.令节点度代价函数为xi(pi)=(ni(pi)-nei(pi))2.其中,当节点i的发射功率为pi时,nei(pi)表示期望节点度,ni(pi)表示节点当前的邻居个数.
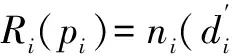
综上所述,定义节点i的收益函数为
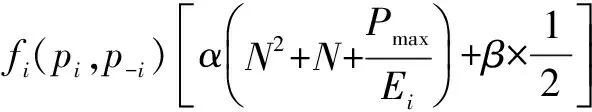
(4)
其中,α,β为权重因子且都是正数.当网络连通时fi(pi,p-i)=1;当网络不连通时,fi(pi,p-i)=0,因此,网络不连通时的收益一定小于网络连通时的收益.当节点发射功率越大时,节点度也会增加,干扰节点也可能会随之增多,节点的剩余能量均衡性会降低;而如果发射功率过小,网络可能无法保持连通状态,因此,这些因素是相互制约相互影响的.
3.2 基于链路质量的拓扑控制博弈分析
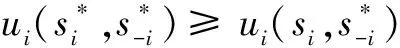
定义2(顺势博弈与顺势函数)[10]对策略型博弈G={I,s,u}而言,如果存在函数V:s→R,对于任意i∈I,pi∈si,qi∈si满足V(pi,p-i)-V(qi,p-i)>0 ⟺ui(pi,p-i)-ui(qi,p-i)>0,那么G就是一个顺势博弈,函数V称为G的顺势函数.
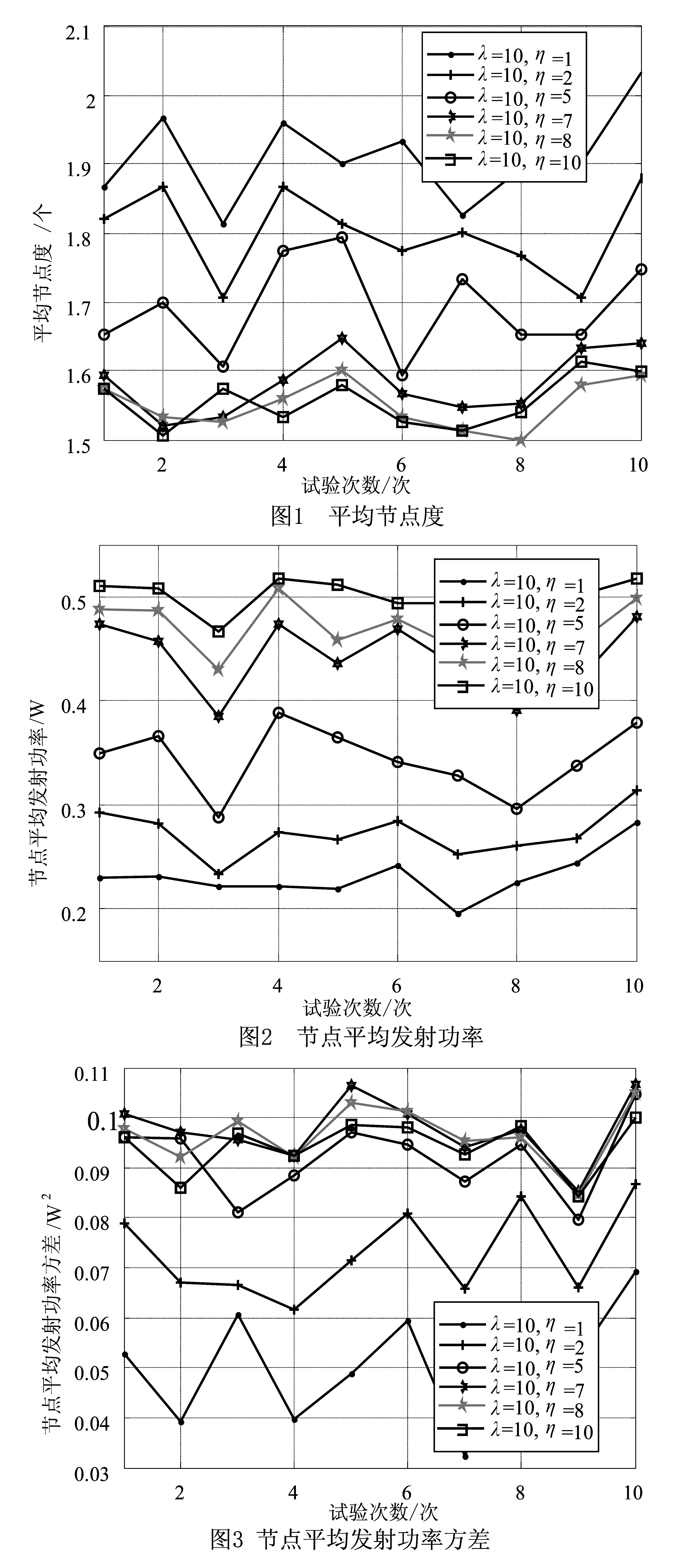
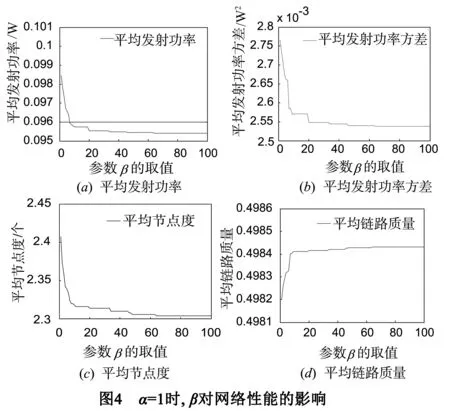
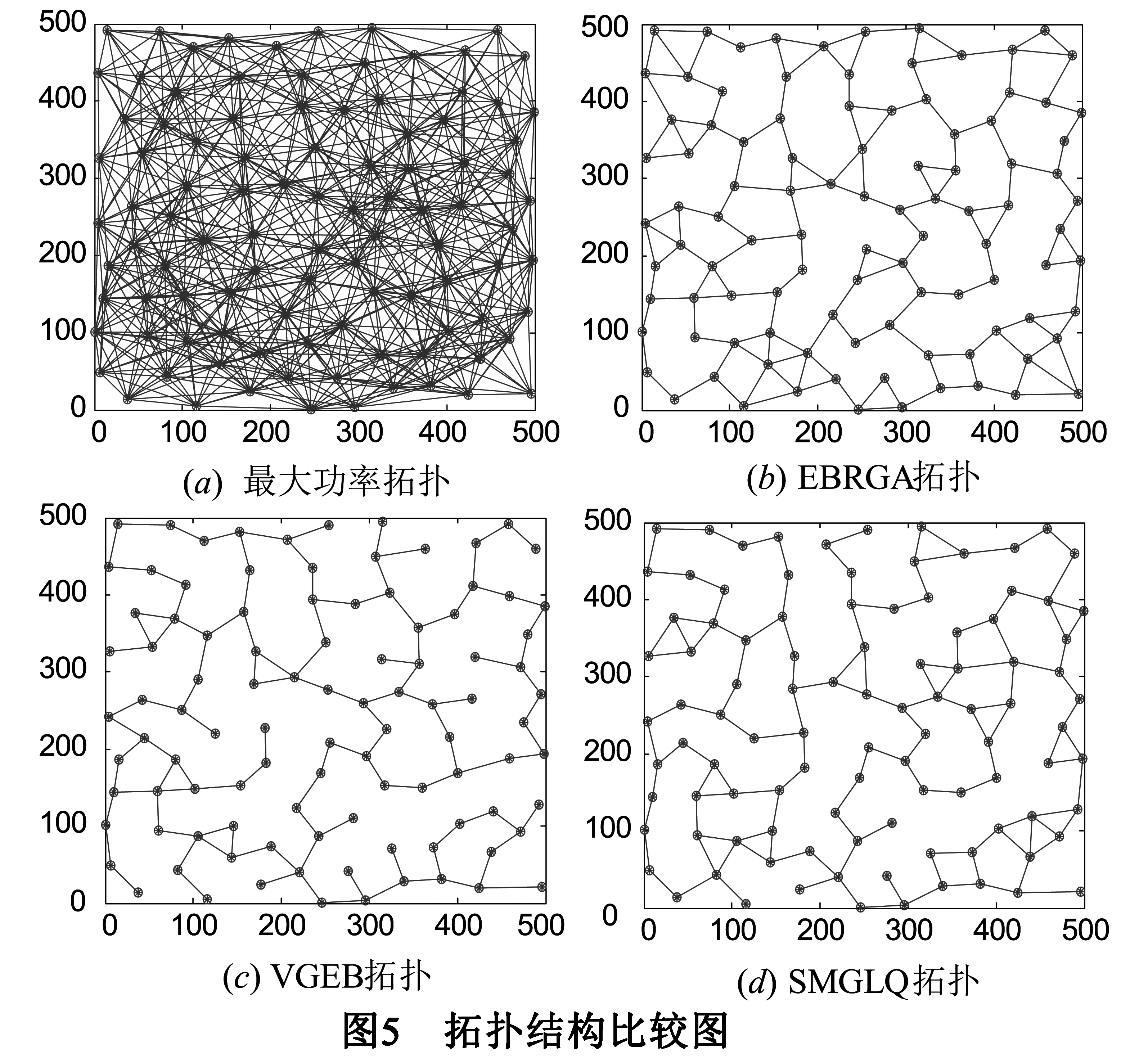
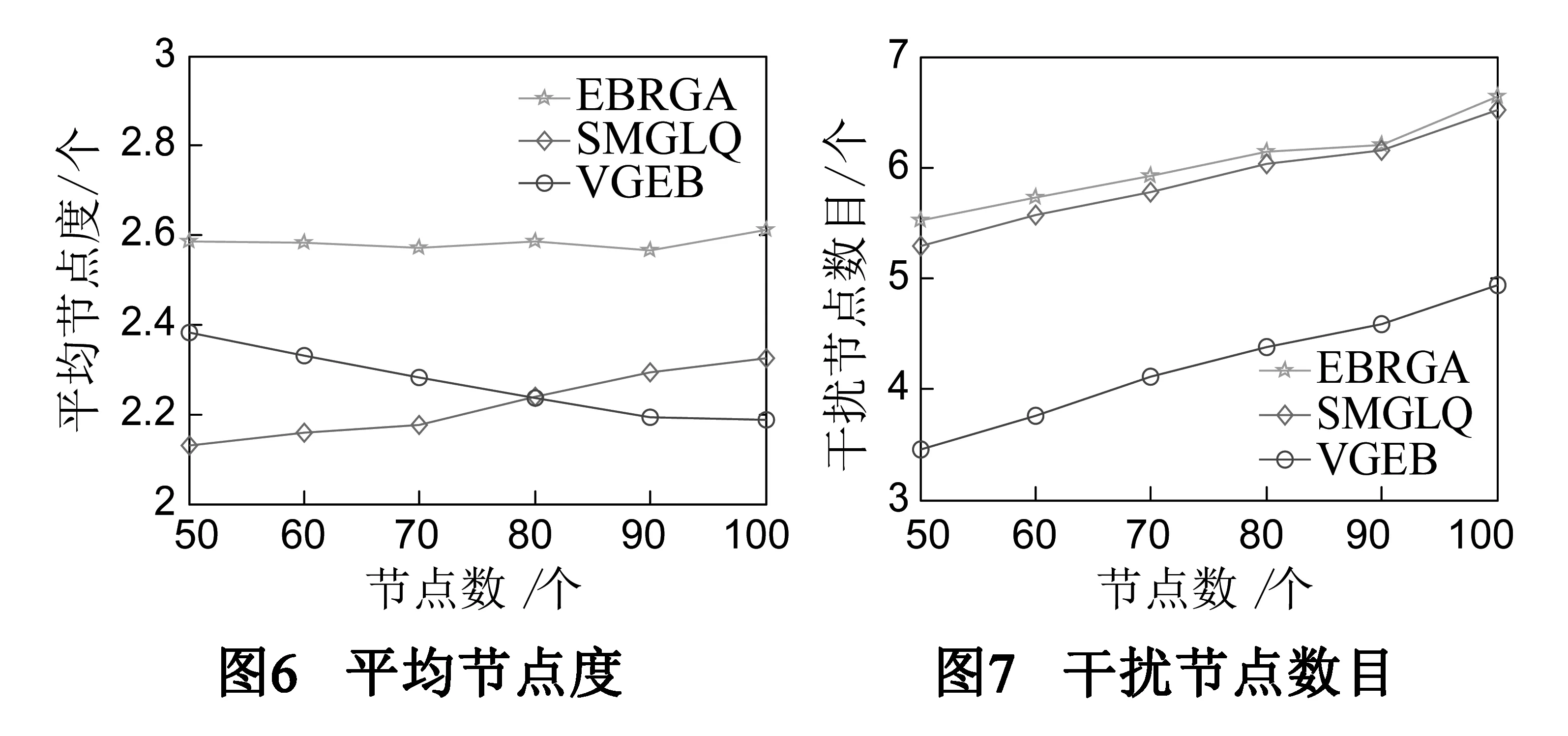
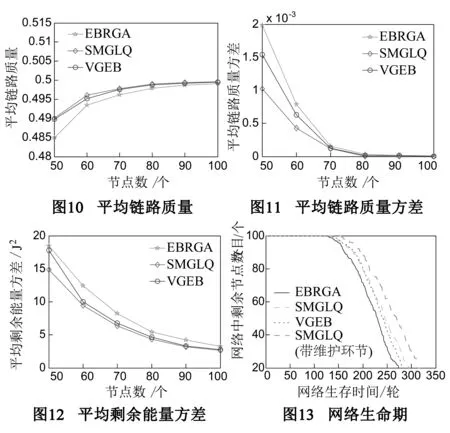
定义3(帕累托最优)[10]如果不存在一个策略集合s′∈s使得任意i∈I满足ui(s*)≤ui(s′),并且uj(s*) 定理1[10]如果策略型博弈G={I,s,u}是顺势博弈且V是其顺势函数,那么使得V最大化的策略组合s*就是博弈G={I,s,u}的一个纳什均衡. 定理2 基于链路质量的拓扑控制博弈模型是一个顺势博弈. (5) 假定pi和qi在节点i可选功率集内,且满足条件pi>qi.根据公式(4)所定义的收益函数可知,当节点i分别选择pi和qi作为功率时的收益差为 (6) 顺势函数之差为 ΔV=V(pi,p-i)-V(qi,p-i) (7) 由于连通代价因子是单调的,因此当pi>qi,fk(pi,p-i)>fk(qi,p-i)时,Δui>0,此时,Δui与ΔV同号;在fk(pi,p-i)=fk(qi,p-i)时,ΔV的第一项为0,此时,ΔV=Δui.由此根据定义2可知V(pi,p-i)是一个顺势函数,G={I,s,u}是一个顺势博弈. 推论 基于链路质量的拓扑控制博弈模型一定存在纳什均衡解. 证明 由定理2可知该模型是顺势博弈,因此,使得顺势函数V(pi,p-i)最大化的策略组合就是纳什均衡解.网络中任意节点i的发射功率pi∈(0,Pmax],因此,一定存在能够使顺势函数V(pi,p-i)最大的策略组合.根据定理1,基于链路质量的拓扑控制博弈模型一定存在纳什均衡解. 拓扑控制算法SMGLQ的实现需要建立在传感器节点满足如下几个条件的前提上:①节点在部署时能量初值不同;②节点具有一定的运算与储存能力,可获取自身的发射功率,接收功率以及当前剩余能量状态;③节点的发射功率可调,且最大功率一致;④互为邻居的节点对满足双向通信;⑤每成功接收到一个数据包,节点都能直接测得其相应的RSSI,LQI和接收功率pr. SMGLQ共分为四个阶段:邻居发现阶段,拓扑构建阶段,功率确定阶段和拓扑维护阶段. 4.1 邻居发现阶段 网络中所有节点依次以最大发射功率Pmax广播Hello消息,其中包含节点的ID编号,当前发射功率Pmax,节点当前能量值Ei.任意节点j收到节点i发送的Hello消息后,先读取相应的RSSI(i,j)和LQI(i,j),然后计算i与其正常通信时所需的最小发射功率pmin(i→j).节点j将自身的ID编号,当前发射功率Pmax,当前能量值Ej,pmin(i→j),RSSI(i,j)和LQI(i,j)打包为Ack消息回复给i.当i收到Ack消息之后,先读取相应的RSSI(j,i)和LQI(j,i),然后解析Ack消息,按照式(2)计算链路ij的通信质量;最后按表1的形式将节点j加入自己的邻居列表Ti当中.其中,各节点的初始收益值均为-∞. 表1 节点i的邻居列表 4.2 拓扑构建阶段 当网络中节点的邻居列表都建立完成以后,节点i按照pmin(i→j)的值对Ti中的所有邻居(m个)进行升序排序.在排序过程中,计算并统计当前发射功率下的邻居节点数目ni(pmin(i→j)),期望节点度nei(pmin(i→j)),链路质量Lq(ij).之后,网络中每个节点以符号T标记自身,开始博弈过程,依次判断自身当前功率对网络连通状况造成的影响.i设置参数numi=1,从邻居列表中第一个邻居Ti(1)开始算起,此时i的功率为pi(i→Ti(1)),判断网络当前的连通状况:⑴如果网络在当前功率时不连通,令连通因子为0,修改Ti中相应的收益.此时,如果numi=m,那么i维持原功率;如果numi 对于网络中任意节点i,当numi≠1时,设置numi=numi-1且pi(i→Ti(numi)),判断此时网络是否连通:如果不连通,那么设置numi=numi+1,此时节点i的发射功率为pi(i→Ti(numi)),并用F标记自身.如果此时网络连通,则功率等级不变.标记自身为F的点i,如果Ti中具有满足pi(i→j)>pi(i→Ti(numi))的任意节点j,则按照收益函数修改Ti中对应的收益.当任意节点i的都以F标记过自身之后,博弈结束. 4.3 功率确定阶段 在经过拓扑构建阶段之后,节点i计算并存储了满足网络连通的各级功率所对应的收益.i比较所有收益,根据最佳回应策略设置自身功率pi ui(pi,p-i)=maxui(pi(i→j),p-i(i→j)),j∈Ti (8) 研究表明,RSSI与发送节点的发射功率近似成线性关系.因此,当网络中任意节点按式(8)重新确定了自己的发射功率后,链路的通信质量虽然没有改变,但是度量指标Bi-CQ会发生变化.节点i按自身当前发射功率pi广播一条包含自身ID的请求消息Request.当j收到Request后,读取该信息相应的RSSI(i,j)和LQI(i,j),计算CQ(i,j)并将其与pj一起打包成Ack消息发送给i.i收到Ack消息后,读取相应的RSSI(j,i)和LQI(j,i),解析Ack消息,按照式(2)计算Bi-CQ(i,j),更新Ti.4.4 拓扑维护阶段 拓扑构建完成后,随着网络运行,节点剩余能量会变得不均衡.此外,可能出现的各种突发状况也会影响链路的通信质量,造成误码率增加甚至于数据包丢失.因此,应随着实际情况调整拓扑. (1)当节点i检测到自身能量等级降低之后,使用Pmax广播剩余能量检测请求消息(SED)取当前通信范围内邻居节点的剩余能量.认为没有回复SED消息的节点已死亡,标记为D. (2)在网络运行过程中,每收到一个数据包,都计算相应的CQ.如果节点i与其邻居j进行通信时,链路质量突然从Bi-CQ(i,j)大幅度下降,那么i标记j为可疑节点SN,链路ij为可疑链路SL后继续通信.如果在后续5次通信过程中,链路质量恢复到原有水平,则撤销对节点j以及链路ij的标注,继续正常通信.而如果在后续5次通信过程中,链路质量持续下降或者发生很大波动,则中断链路ij,i从邻居列表中删除节点j. 在这两种情况下,节点i根据收集到的最新数据重新博弈,选择当前状态下使得收益最大的功率作为发射功率pi.判断此时网络连通性:如果网络连通,那么i采用pi继续通信;如果此时网络已不连通,那么节点i清空自身邻居列表并以Pmax广播网络重构消息(Reconsitution),标记自身为T.收到重构消息的节点清空自身邻居列表并以Pmax广播重构消息,标记自身为T;已标记自身为T的节点不再广播重构消息.当网络中所有节点都以T标记自身之后开始重新构建拓扑,转至4.1. 5.1 算法证明 为便于书写,将最大功率拓扑表示为Gmax,SMGLQ算法构建的拓扑结构表示为GSMGLQ. 定理3 SMGLQ能使节点收敛至纳什均衡. 证明 推论表明基于链路质量的拓扑控制博弈模型存在纳什均衡,其对应的顺势函数如式(4),即V是网络中所有节点的收益总和.由于在功率确定阶段,网络中任意节点均选择了能使自身收益最大的功率,所以,这些收益总和是最大值.至此,各节点功率组合就是SMGLQ的纳什均衡解. 定理4 如果Gmax连通,那么GSMGLQ也连通. 证明 在定理3中已经证得在执行完SMGLQ后网络中各节点均收敛至纳什均衡.设节点i达到纳什均衡时的功率为pi,那么肯定存在pi ui(pi,p-i)-ui(Pmax,p-i)≥0 (9) 由于Pmax一定能保证网络连通,因此 ui(Pmax,p-i) (10) 采用反证法,假设i选择功率pi时网络不连通, (11) 此时 (12) 定理5 SMGLQ能收敛到帕累托最优. 证明 由无线传感器网络的特性可知,当节点发射功率增大或减小时,其干扰节点数目,邻居节点数目随之增大或减小,因此∂Ri(pi)/∂pi>0,∂ni(pi)/∂pi>0.下面首先分析收益函数. (1)当nei(pi)=max(4ω×EDev(i),ni(pi))=ni(pi)时,对收益函数进行求导 (13) (2)当nei(pi)=max(4ω×EDev(i),ni(pi))=4×EDev(i)时,对收益函数进行求导 (14) 因此,收益函数ui(pi,p-i)与发射功率pi的关系为 (15) 因此,ui(pi,p-i)是发射功率pi的单调减函数. 首先根据纳什均衡定义可知,没有一个节点可以通过降低自身功率来获取更高的收益,如果强行降低功率只会降低自身收益,甚至使得网络无法连通.其次,不存在k(k≥2)个节点在保证网络连通的条件下同时降低发射功率来增加自身收益.这是因为如果存在节点i可以通过降低自身发射功率pi,从而减小ni(pi)来增加收益,那么必然存在节点j为了保持网络连通性而增大自身发射功率pj,由于收益函数uj(pj,p-j)是减函数,那么j的收益必然减小,更何况k个节点同时降低自身功率以获取更大收益了.因此不存在任意节点在能不降低其他节点收益的情况下增大自身收益.即SMGLQ算法达到的纳什均衡是帕累托最优的. 5.2 性能分析 λ,η表示其对应部分在CQ中的比重,确定它们的取值对CQ有很大意义,首先通过仿真实验分析λ,η对CQ的影响规律.将50个节点随机分布在500m×500m的区域,将Bi-CQ作为链路质量指标,采用EG模型搭建拓扑.设定最大传输范围为150m.令λ=10,分别为η赋值为1,2,5,7,8,10,进行10次仿真实验对比网络性能,选取最佳的参数组合,如图1所示.由于节点发射功率与最大发射功率的比值表明了发射功率的相对大小,不受最大发射功率值的限制,因此,本文均采用发射功率与最大发射功率的比值表示节点发射功率.由图1可知,当λ=10时,网络平均节点度随着η的增大而减小;图2表示网络中的平均发射功率随着η的增大而增大.在图3中,网络中平均功率的方差随着η的增加而增大.因此,综合拓扑结构的各方面性能,选取组合λ=10,η=5. 由于EBRGA也是以节点自身各项性能的相互制约相互影响来构建拓扑的,因此将EBRGA作为对比算法;VGEB算法无需节点信息实时交互,可最大程度降低能耗,因此也将其作为对比算法,验证SMGLQ拓扑控制算法的可行性和有效性.首先分析收益函数中α,β值对拓扑性能的影响.随机布撒100个节点在500m×500m的区域内,最大传输半径设为150m.求取性能参数,通过5次实验数据取平均值进行分析来确定α,β的值.因此,首先令α=1,通过改变β的取值来观察参数α,β对网络性能的影响,如图4所示.从图4(a),4(b)中可以看出,β=100时平均发射功率与平均发射功率方差都较小,也就是说网络具有较小能耗.此时平均链路质量较高,平均节点度曲线也较为稳定.因此,将权重因子设置为α=1,β=100. EBRGA算法中并没有拓扑维护部分,VGEB算法也并没有给出详细的维护过程.为方便比对,在拓扑结构和性能分析(1)~(6)的仿真比较过程中并未加入拓扑维护环节.在500m×500m的区域内随机布点100个,最大传输半径设为150m.分别执行SMGLQ,EBRGA和VGEB算法,得到的拓扑结构如图5所示.可知,由于这三种算法选择链路时遵守的准则不同,所形成的拓扑结构也不同.EBRGA拓扑链路较为密集,VGEB拓扑较为稀疏,SMGLQ拓扑则位于两者之中. 在300m×300m的区域内分别布点50,60,70,80,90,100个,以100m为传输半径.分别执行100次EBRGA算法,VGEB算法,SMGLQ算法来构建拓扑,对网络进行性能分析. (1)平均节点度比较.由图6可知,EBRGA算法的平均节点度随网络规模变化不大,这是由于其期望节点度为3.随着节点密度的增大,VGEB算法的平均节点度呈下降趋势,而SMGLQ算法的平均节点度不断上升,在网络密度较大时,SMGLQ算法能更好的保证网络鲁棒性. (2)平均干扰节点数比较.随着网络密度的增大,图7中的平均干扰节点数曲线都在上升.其中,EBRGA算法干扰过大,VGEB算法干扰节点过少降低了网络鲁棒性,SMGLQ拓扑的干扰节点数目居中,能降低干扰并增强网络鲁棒性. (3)平均发射功率比较.从图8中可以看出,平均发射功率曲线都随着网络密度的增大而减小.VGEB算法仅以降低能耗为优化目标,因此具有较低的发射功率.与EBRGA算法相比,SMGLQ算法在通过降低发射功率减小网络能耗方面具有更好的性能. (4)平均发射功率方差比较.如图9所示,随着网络密度的增大,节点平均发射功率方差呈递减趋势.VGEB算法的收益函数仅与功率相关,因此在能耗均衡性方面也具有优势.SMGLQ拓扑的平均发射功率方差小于EBRGA拓扑,因此,SMGLQ算法在能耗均衡方面优于EBRGA算法. (5)平均链路质量比较.EBRGA,VGEB算法中并没有定义链路质量,为方便对比,本部分采用节点使用最大功率时各链路对应的评价指标Lq为EBRGA与VGEB中的链路质量赋值.从图10中可以看出,随着网络密度的增大,这三种算法所构建的拓扑中链路质量均增大.相比而言,SMGLQ拓扑的平均链路质量更大一些.图11中的平均链路质量方差曲线则表明,在网络密度较小时,由于可供选择的链路较少,链路质量相差就比较大;当可选链路较多时,链路质量比较均衡. (6)剩余能量方差比较.如图12所示,平均剩余能量方差曲线随节点数目的增加而减小.其中SMGLQ算法的平均剩余能量方差最小,这说明它可以为节点选择剩余能量较为均衡的邻居. (7)网络生命期比较.本文定义当网络中死亡节点数超过总节点数的20%以后,网络死亡.将100个节点布撒在区域内,分别使用EBRGA算法,SMGLQ算法,VGEB算法构建拓扑.由图13可以看出,首先出现死亡节点的是EBRGA拓扑.随着网络运行,这三种拓扑的死亡节点数目都不断增加.无维护环节的SMGLQ算法与VGEB算法生命期相差不大.拓扑维护的目的就是使网络始终处于最优或者接近最优的状态,最终达到延长网络生命期的目的.由图13可看出加入维护环节后,SMGLQ算法的生命期被显著延长,这也说明了拓扑维护的必要性. 本文首先定义了一种表征链路双向通信质量的链路通信质量评价指标.其后,构建了拓扑控制博弈模型,该模型将网络的各项性能指标融入收益函数.理论分析并证明了该模型具有纳什均衡解.最后,本文设计了一种基于链路质量的自维护拓扑控制博弈算法SMGLQ,理论分析表明执行SMGLQ算法能保证网络连通,还能使所有节点收敛到帕累托最优.同时,仿真结果显示SMGLQ算法不仅能选择通信质量好的链路,还能有效减小网络能耗,最主要的是,能显著地延长网络生命期. [1]Hao X C,Zhang Y X,Jia N,et al.Virtual game-based energy balanced topology control algorithm for wireless sensor networks[J].Wireless Personal Communications,2013,69(4):1289-1308. [2]Cho H H,Tseng F H,Shih T K,et al.Ak-cooperative analysis in game-based WSN environment [J].Lecture Notes in Electrical Engineering,2014,260:1215-1225. [3]Guoyan Yang,Xin Guan.A non-cooperative game theoretic approach to energy-efficient power control in wireless sensor networks[J].International Journal of Future Generation Communication and Networking,2014,7(1):169-180. [4]Miao X N,Xu G.Cooperative differential game model based on trade-off between energy and delay for wireless sensor networks[J].Annals of Operations Research,2013,206(1):297-310. [5]郝晓辰,张亚晓,刘彬,等.一种能耗均衡的传感器网络可靠拓扑博弈算法[J].软件学报,2011,22 (Suppl1):1-12.Hao Xiao-chen,Zhang Ya-xiao,Liu Bin,et al.Energy-balanced and reliable topology control game algorithm for sensor networks [J].Journal of Software,2011,22 (Suppl1):1-12.(in Chinese) [6]王绍青,聂景楠.一种无线传感器网络性能评估及优化方法[J].电子学报,2010,38(4):882-886. WANG Shao-qing,NIE Jian-nan.An approach of performance analysis and optimization for wireless sensor networks[J].Acta Electronica Sinica,2010,38(4):882-886.(in Chinese) [7]Xing G,Lu C,Jia X,et al.Localized and configurable topology control in lossy wireless sensor networks[J].Ad Hoc Networks,2013,11(4):1345-1358. [8]Dinh Duong Mai,Anh Tai Tran,Myung Kyun Kim.Measuring link quality based on ETX metric in multi-hop wireless networks[J].Advanced Science and Technology Letters,2014,46(Networking and Communication 2014):115-118. [9]吕涛,施伟斌.无线传感器网络自适应功率调整机制研究[J].信息技术,2014,(3):134-136. LÜ Tao,Shi Wei-bin.Adaptive power adjustment mechanism for wireless sensor networks[J].Information Technology,2014(3):134-136.(in Chinese) [10]Xiao Mi,Shao Xin-yu,Gao Liang,Luo Zhen.A new methodology for multi-objective multidisciplinary design optimization problems based on game theory[J].Expert Systems with Applications,2015,42(3):1602-1612. 陈 白 女,1981生于浙江磐安.河北省燕山大学电气工程学院实验师.研究方向为无线传感器网络拓扑控制算法、信道分配算法. E-mail:chenbai@ysu.edu.cn 辛敏洁 女,1990年生于陕西宝鸡,河北省燕山大学电气工程学院硕士研究生.研究方向为无线传感器网络拓扑控制算法. E-mail:xlxmjysu@126.com SMGLQ:A Self-Maintaining Topology Control Game Algorithm Based on Link Quality CHEN Bai,XIN Min-jie,LIU Wei-jing,YAO Ning,HAO Xiao-chen,RU Xiao-yue (InstituteofElectricalEngineering,YanshanUniversity,Qinhuangdao,Hebei066004,China) In order to overcome the problem that the topology performance optimization of wireless sensor network is single,an indicator which can represent the bi-directional communication quality of a link is defined.Then the link communication quality,node interference and balance of surplus energy are integrated into the utility function.Finally,a self-maintaining topology control game algorithm based on link quality (SMGLQ) is proposed.The theoretical analysis proves that SMGLQ algorithm can converge to a Pareto optimal.Simulation results show that SMGLQ chooses the links with better communication quality for the network.Moreover,it can reduce the energy consumption. wireless sensor network (WSN); topology control; link quality; game theory 2014-07-18; 2015-05-25;责任编辑:梅志强 国家自然科学基金(No.61403336); 河北省自然科学基金(No.F2015203342); 燕山大学青年教师自主研究计划课题(No.13LGA008,No.15LGB007) TP393 A 0372-2112 (2016)09-2227-08 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.09.030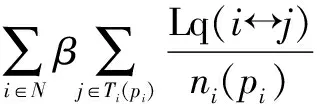

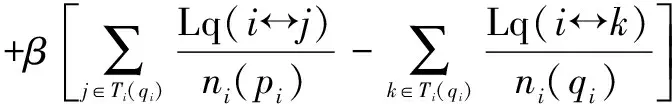
4 拓扑控制算法SMGLQ

5 SMGLQ算法证明与性能分析
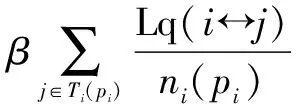
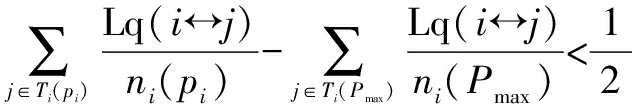


6 结论



