基于校正搜索宽度的极化码译码算法研究
卢丽金, 郑鑫, 张晓洁,李家海,廖东凤
(广西民族师范学院数理与电子信息工程学院,崇左 532200)
0 引言
极化码(polar code)是目前仅有的一种在数学上被严格证明且能实现香农信道容量的信道编码方式[1]。Turbo码作为信道编码方案中的一种,被应用于第三代移动通信系统和第四代移动通信系统。随着无线通信的发展,5G 具有超大容量、超大连接性及零时延的特点,因此需要更好的编码方案。而极化码具有能够达到信道容量、可靠性强、超低时延等特点,是5G 技术急需的编码方案。
为不断提高性能和降低复杂度,各种各样的译码相继被提出。基于提高极化码性能的想法,提出置信度传播[2-3]和线性规划[4]算法。然而, 上述两种算法仅适合应用于二进制输入删除信道(BEC)。针对此情况,串行抵消列表(SCL)译码被提出[5-6],突出搜索宽度(L)的概念,提高译码性能。随后,CRC 辅助的串行抵消列表(CASCL)译码被提出[7-10],利用循环冗余校验码来辅助译码,降低译码复杂度同时进一步提高译码性能。为了深入改进SCL 译码,自适应的串行抵消列表(AD-SCL)译码被提出[11],与CA-SCL 译码相比,显著降低了平均译码复杂度。
AD-SCL 译码在保证性能不变的前提下,出现了明显的时延问题。从AD-SCL 译码思路这个角度来分析,可以得出结论:给定一个最大的L值(Lmax)并设置L的初始值为1,从L=1 开始执行译码;随后,对得到的L条译码候选路径进行循环冗余校验,当通过校验时退出译码,反之,将原来的搜索宽度更新为2 倍搜索宽度,同时退回到root节点继续执行译码,直到L=Lmax。在这一整个过程中,一方面,AD-SCL 总是把L的初始值设置为1;另一方面,一旦译码候选路径不能通过CRC 校验,L会不断地更新为2L并返回到根节点继续进行译码。综合考虑这两方面的影响,将会引起非常高的时延。L=1 时, AD-SCL 译码算法相当于串行抵消(SC)译码算法。误码率相当高,译码性能亦不理想。针对上述存在的时延问题,假设改变L的初始值总是设置为1 的思路,并且减少执行SCL 译码的次数,那么,将能够显著降低时延。因此,将搜索宽度作为切入点,调整、校正搜索宽度成为研究的关键。
本文提出了一种基于校正搜索宽度的极化码译码算法。该算法采用跟踪历史数据、采集历史数据以及对符合条件的历史数据进行数学运算的方法,不断调整、校正搜索宽度,降低执行串行抵消列表译码的次数,进而降低极化码解码时延,提高解码效率。实验结果表明在保持性能不变的前提下,该算法能明显降低解码代价和时延。
1 基础原理
1.1 译码
SC 译码的缺点是复杂度低,优点是译码结构简单。当码长N足够大时,理论上SC译码一直被证明能够达到Shannon 容量;反之,其纠错性能常常是不理想的。针对这个问题,提出了SCL 译码。它是SC译码算法升级版中的一种,能用相对低的复杂度来获取最大似然译码性能。
一般地,SCL 译码算法的思想以码树的形式来呈现。图1 为SCL 译码的码树形式。以图1 为例,一棵深度为4 的满二叉树,看成是码长为4的Polar码。除叶子节点外,每一层边都分别标记一个1或0,其中1表示信息比特,0为固定比特。以root 节点为出发点,任一叶子节点为终点,长度为N的路径形成一条译码序列(包含固定比特)。
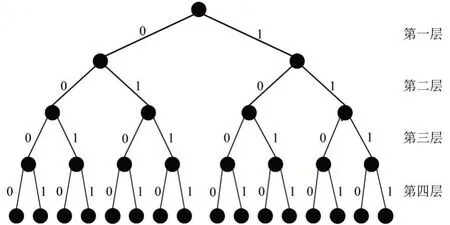
图1 SCL译码的码树形式
以L=4,N=4为例,简单介绍SCL译码算法的译码过程,具体如图2所示。
结合图2,将SCL 译码算法的译码过程归纳为:
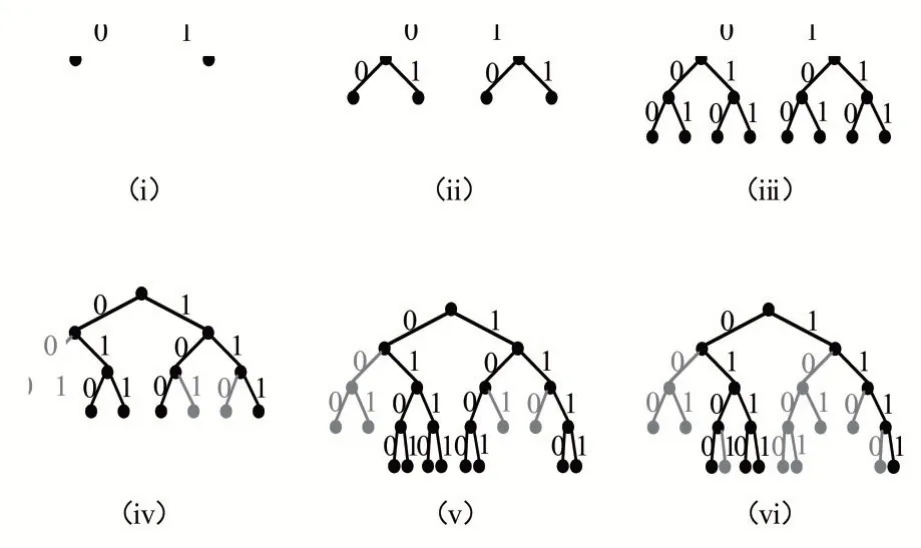
图2 SCL译码的具体过程
(1)与SC 译码算法类似,从根节点开始,逐层进行路径搜索。
(2)当经过第一层边的扩展时,存在两条候选路径(如图2(i)),由于L=4,所以把这两条候选路径都保留下来。
(3)当进行第二层边的路径扩展时,产生四条译码候选路径(如图2(ii)),由于L=4,所以把这四条候选路径都保留下来。
(4)当经过第三层边的扩展时,存在八条候选路径(如图2(iii)),因L=4,所以只需要保存最有可能的四条译码候选路径,同时舍弃掉其余四条候选路径(如图2(iv))。
(5)当经过第四层边的扩展时,存在八条候选路径(如图2(v)),因L=4,所以只需要保存最有可能的四条译码候选路径,同时舍弃掉其余四条候选路径(如图2(vi))。
(6)最后,从保留的四条候选路径里,选出一条具有最大度量值的候选路径,作为译码结果输出。
1.2 基本公式
谈及SCL 译码算法时,对数似然比(LLR)和路径度量值的计算必不可少[12-13]。
那么,LLR的表达式如下:
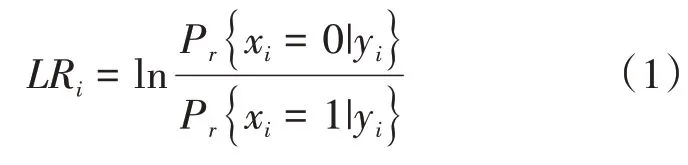
其中,xi为输入信号。yi是接收信号。相应地,LLR的递归计算方法如下:

经过变换,采用以下公式递归地计算,可以得到路径度量值:

2 基于校正搜索宽度的极化码译码算法
因极化码能够达到信道容量,故其编译码技术都受到了广泛关注。随着移动通信系统的快速发展,SC、SCL、CA-SCL、AD-SCL 等译码方法随之出现。在保证性能不受影响的前提下,实现平均译码复杂度能够大幅度降低的愿景,ADSCL 总会将搜索宽度的初始值配置为1。当L=1 译码失败时,该算法会将L=1 直接更新为L=2,退回到根节点,重复前一轮的译码操作。若L=2时,译码还不成功,则会将L=2 更新为L=4,继续进行译码。一般地,在AD-SCL 的译码过程中,产生几个不同的搜索宽度值是正常现象。假设将搜索宽度的初始值设置成1 时,这时的AD-SCL 译码相当于SC 译码。由于SC 译码是逐比特译码,故一旦有一个比特判决有误,那么在之后的译码过程中都将处于错误的子树中执行译码。综合讨论,SC 译码固然能实现平均译码复杂度显著降低的愿景,但却失去性能方面的优越性。经过基于L=1的译码后,往往还需要更新L值。这样无疑增加了时延。当译码需要更新搜索宽度时,一定程度来说不止更新一次。如当Lmax= 32 时,至多会更新5次左右。换个角度来理解,当Lmax= 32时要进行6 次SCL 译码算法。因此,更新次数多是存在高时延的原因之一。因此,如何解决高时延问题成为本文研究内容。而调整、校正搜索宽度是解决高时延的重要切入点。
2.1 确定搜索宽度的理想初始值
本文提出一种能减小时延、降低复杂度的SCL 译码算法。新算法与传统算法的主要区别在两方面。第一方面,L的初始值的大小不固定成1;第二方面,当搜索宽度设置为初始值时,译码失败后并不会放弃译码或者直接更新为2 倍搜索宽度。为更好地理解,将搜索宽度进行初始化时的值标记为Li。同样地,对搜索宽度执行初始化操作在新算法里也是需要的,不一样的是Li不总是等于1,Li的大小会视具体情况进行变化。信道质量不同,成功译码时所对应的L 值也会有所不同。假设能在理想的Li下译码,那么,译码的成功率也将会与之俱增。此时,既能够保证译码性能,同时又能降低译码时延,是一种理想的搜索宽度。为此,将这一理想的Li称为搜索宽度的理想初始值,并记为Loi。因此,想要降低时延需调整、校正搜索宽度,确定搜索宽度的理想初始值。
虽然显著地提高译码性能和极大地降低译码复杂度很难同时兼得,但是,通过不断调整、校正搜索宽度,获取搜索宽度的理想初始值Loi,能使性能和复杂度最大可能实现双赢。本文提出的Loi通过跟踪历史数据、采集历史数据以及对合格历史数据进行数学运算的方法来确定。下面首先对上述所提历史数据作一下说明;其次,阐述Loi的具体确定方法。为易于理解,文中给定Lmax= 32。
对于一次实验来说,若将总帧数记为TN,则本实验给定的总帧数为TN= 100000。将Loi、译码成功时的搜索宽度值(Ls)等数据记录下来,完成对历史数据的跟踪与历史数据的采集。第q帧对应的Ls用Ls[q]来表示,1 ≤q≤TN。因此,本文所谓的历史数据指的是被记录下来的数据,包括Loi,Ls等。同时,将第q帧对应的Loi用Loi[q]来标记。
通过五个阶段来确定搜索宽度的理想初始值Loi。将TN均匀地分为五组,每一组帧对应着一次实验中的一个阶段。五个阶段的划分情况如下所示:

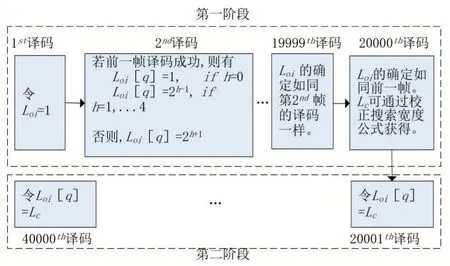
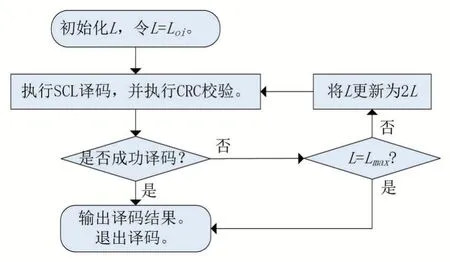
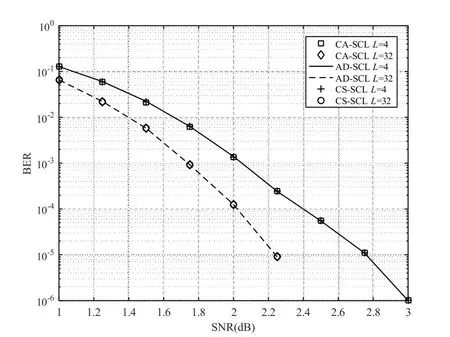
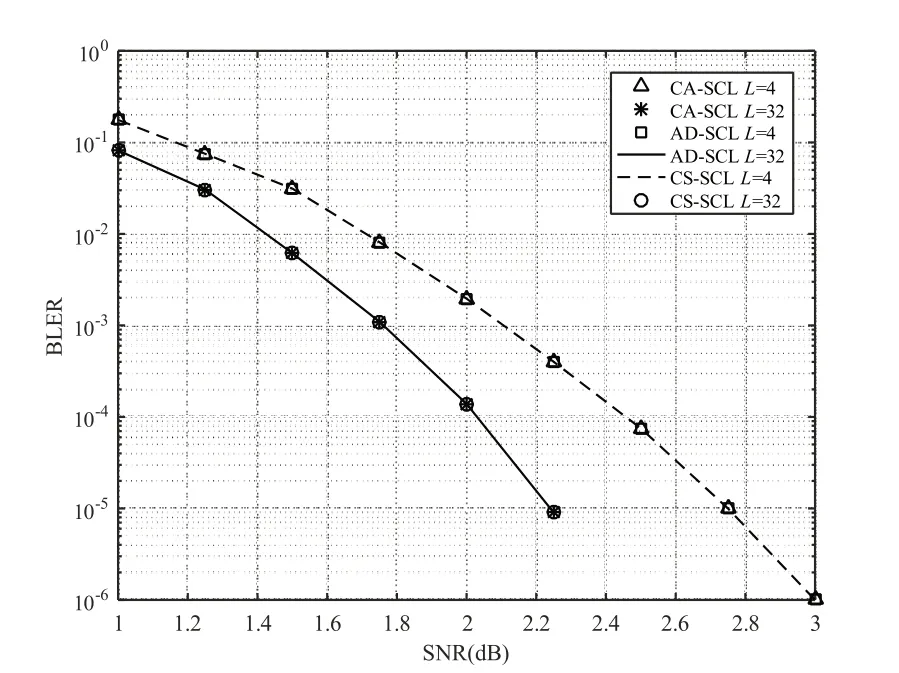
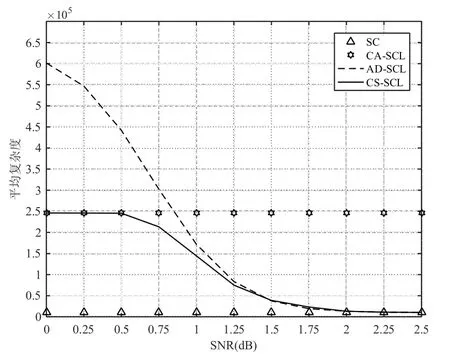
首先分析第一阶段。第1 帧、第2 帧和第20000 帧尤为关键。注意,对于第1 帧,需要令L=Loi= 1。一般地,译码有成功和失败两种情况,无论是译码成功还是译码失败,均需将Ls[1]记录下来。注意,本文规定Ls[q]= 0 代表译码失败。当译码运行到第2 帧时(q= 2),前1 帧译码成功时,对Loi[q- 1]作一个判断,若Loi[q- 1]=1, 则 令Loi[q]= 1; 若 1 若前一帧译码失败时,当前的理想初始值为: 同样地,需要将Ls[q]记录下来。类似地,第3~19999 帧的操作,如同第2 帧。在第20000 帧,对于初始值的设置与记录工作,它们的操作与第2~19999 帧相同。不同之处在于,在第20000 帧中加入校正搜索宽度(CSW)公式,该公式为: 其中,Loi= 20,21,…,24,PLs表示当L=Loi时译码成功的概率。校正搜索宽度的用意在于校正执行完一次译码对应的的搜索宽度。通过记录得到20000 个Ls,分别计算PLs=1,PLs=2,PLs=4,PLs=8,PLs=16。假设统计出Ls= 1,Ls= 2,Ls= 4,Ls= 8,Ls= 16的个数分别为an,bn,cn,dn,en,则它们对应的概率分别计算为:。并将Loi与PLs代入校 正搜索宽度的校正公式中,则有: 将CSW1,CSW2,CSW4,CSW8,CSW16作 一下对比,选出一个最小值。选出的CSWLoi的最小值所对应的Loi记为Lc,并作为下一帧的Loi,即Loi[q+ 1]=Lc。至此,完成第一阶段的Loi的确定。 基于第一阶段的分析, 可得到Loi[20001] =Lc。第20002~39999 帧的操作如同第一阶段中的第二帧一样。第40000 帧的操作如同第20000 帧的操作一样。因此,在第三、四、五阶段中,涉及的操作都如同第二阶段的操作一样。显而易见,Loi的确定已全部完成。注意,这TN帧里,每一帧都对应着一个Loi。通过历史数据来确定Loi,实质上就是根据信道的实际情况来确定的。结合信道实际情况,Loi的确定可以达到最理想化,最终实现性能与复杂度的最佳平衡。为便于理解搜索宽度理想初始值的确定过程,绘制了一个过程框图。 图3 绘制出第一阶段和第二阶段的理想初始值的确定过程框图。那么,在第三、四、五阶段中,涉及的操作都如同第二阶段的操作一样。 图3 理想初始值的确定过程 在保证译码性能不受影响的前提下,进一步降低极化码译码时延,本文提出基于校正搜索宽度的SCL(CS-SCL)译码算法。该算法亦可称为两步走算法。前面的文章内容已经介绍如何确定搜索宽度的理想初始值Loi。那么,两步走方案可以大致理解为,首先是执行基于L=Loi的译码;若译码失败,会将L=Loi更新为L=Lmax,并执行基于L=Lmax的译码。换句话理解,本课题的算法最多只需要进行2 次串行抵消列表译码方案,进而实现显著减少时延的的愿景。 本文提出的CS-SCL 译码算法的详细步骤如下所示: (1)初始化:令L=Loi。 (2)计算度量值与路径扩展:执行SCL 译码算法,同时CRC校验。 (3)译码路径判决:若通过CRC 校验的候选路径数大于等于1 时,则输出具有最大度量值的一条路径,同时退出译码;否则,跳到(4)。 (4)更新判决:判断搜索宽度L是否等于Lmax,若L不等于Lmax,则把L=Loi更新为L=Lmax,并跳回(2);否则,退出译码。 为帮助梳理思路, 基于校正搜索宽度的极化码译码算法的流程如图4。 图4 CS-SCL译码算法流程 通过分析仿真结果,对CS-SCL 译码、SC 译码、CA-SCL 译码、AD-SCL 译码进行性能和复杂度对比。本文拟用文献[14]中的构造方案来对极化码进行构造。在本次仿真试验里,几种译码方案将会接收到一样的的码字。译码的性能和译码的复杂度被用来衡量与验证CS-SCL 译码算法,那么,误块率(BLER)、误比特率(BER)以及平均复杂度是衡量与验证算法必不可少的几个评估指标。下面将通过这三个评估指标来对实验得到的仿真数据进行综合分析、总结归纳译码优劣。 如图5,将几种译码算法的码长配置为N=1024,码率均为R= 0.5,且列表译码的搜索宽度分别设置成L= 4 与L= 32。在不同列表大小下,对各条BER 曲线进行对比发现,CS-SCL 译码与CA-SCL 译码、AD-SCL 译码几乎是重叠在一起的。总结可知, CS-SCL 译码方案在上述配置下也能像CA-SCL译码、AD-SCL译码一样获得非常逼近ML译码的性能。 图5 CS-SCL译码与其他译码方案的BER对比 与BER 曲线类似,在不同列表大小下,对各条BLER 曲线进行对比发现,CS-SCL 译码与CASCL 译码、AD-SCL 译码几乎是重叠在一起的,如图6。详细地,当L=4 时,CA-SCL、AD-SCL与CS-SCL 的BLER 曲线是重叠的;当L=32 时,CS-SCL、CA-SCL与AD-SCL的BLER曲线也是重叠在一起的。这一重叠现象进一步阐明了CSSCL 译码方案能够获得与CA-SCL、AD-SCL 译码方案几乎一致的译码性能。 图6 CS-SCL译码与其他译码方案的BLER对比 如图7,将几种译码算法的码长配置为N=1024,码率均为R= 0.5,且列表译码的搜索宽度被配置为L= 32。当SNR 越来越大时,CSSCL 译码的平均复杂度曲线几乎与SC 译码的平均复杂度曲线相互重叠。经过对比可知,CSSCL 译码可以明显地减小平均复杂度,尤其在高信噪比下,CS-SCL 译码非常逼近SC 译码。通过测量平均计算复杂度来评估译码复杂度,相当于需要测量路径度量递归操作的次数。当SNR 的范围为0~1.0 dB 时,CS-SCL 译码比AD-SCL 译码能更大幅度减小平均复杂度。当SNR=0 dB 时,CS-SCL 译码的复杂度可以降低约57.8%;当SNR=1.0 dB 时,CS-SCL 译码的复杂度可以降低约13.8%。综上所述,在低SNR 下,CS-SCL 译码能够在保证译码性能不受影响的前提下显著地降低平均复杂度。在低SNR 下,CS-SCL 译码能够非常接近ML 译码性能,同时能极大地降低译码时延。 图7 CS-SCL译码与其他译码的平均复杂度对比 仿真实验涉及到的译码包括:SC、CA-SCL、AD-SCL、CS-SCL 译码算法。实验数据表明,一方面在不同列表大小下,CS-SCL、CA-SCL、AD-SCL 译码拥有几乎相同的BER 与BLER 性能,且可以非常接近ML 译码性能。另一方面,当SNR=0dB 时,CS-SCL 译码的复杂度可以降低约57.8%;当SNR=1.0 dB 时,CS-SCL 译码的复杂度可以降低约13.8%。在低SNR 下,CS-SCL 译码能大幅度降低译码时延。

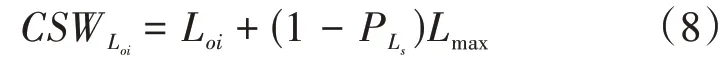
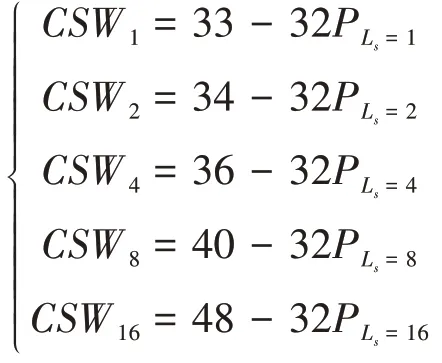
2.2 基于校正搜索宽度的SCL译码算法
3 仿真结果与分析
4 结语

