跳扩散过程下选择期权的定价

王心悦，李翠香，刘淑娟

(河北师范大学 数学科学学院， 河北 石家庄 050024)

近年来，金融衍生产品市场迅速崛起，出于各种各样的目的，出现了多种金融衍生产品，例如：交换期权、复合期权、重置期权、亚式期权、选择期权等。期权定价和对冲问题也成为了金融领域的一个重要主题，吸引了国内外学者的关注。Black和Scholes[1]在1973年提出了著名的Black-Scholes(BS)定价模型，模型假设无风险利率r及波动率σ为常数。但众所周知，无风险利率和波动率是随着时间变化而改变的，假设其为常数,则存在着极大的局限性，并不符合实际情况。文献[2]考虑了当利率和波动率依赖于时间时复合期权的定价问题。对于一些期限较长的期权而言，假设利率是关于时间的确定函数也是不太合理的，建立随机利率模型十分必要。李淑锦等[3]借助测度变换推导了在随机利率模型下复合看涨期权和重置看涨期权的定价公式。另外，由于受到突发事件的影响，资产价格表现出跳跃的特性，在对衍生产品定价时，一些学者考虑假设标的资产价格满足跳扩散模型。Peng等[4]、刘佳玥等[5]、吴桑等[6]、刘庆伟[7]分别得到了跳扩散模型下不同期权的定价公式。

选择期权是指在期权有效期内的某个确定时刻，其持有者有权决定到期的是一份看涨期权还是一份看跌期权。选择期权赋予了持有者更多的权利，能降低期权持有人的风险，它的这一特性引起了许多学者的关注。邓国和[8]考虑了Heston模型下选择期权的定价问题。黄国安等[9]给出了当标的资产价格服从跳扩散模型时选择期权的价格公式。

本文将考虑当资产价格服从跳扩散过程，贴现债券价格服从几何布朗运动时选择期权的定价问题。期权价格是在风险中性测度下到期收益期望的贴现值，通过构造等价鞅测度将计算期望转化为计算概率，同时服从跳扩散过程的随机变量一般不具有显式形式的密度函数，而其特征函数容易求得，分布函数和特征函数之间具有一定关系，可以利用特征函数表示期权的价格。

1 预备知识

本文假设Q是风险中性测度,(Ω,F,{Ft}t≥0,Q)是带域流{Ft}t≥0的概率空间，其中Ω表示样本集，Ft⊆F,{Ft}t≥0是由本文所涉及到的随机过程所生成的。

设r(t)表示无风险利率，并且是随机的，P(t,T)为到期日为T的贴现债券在t时刻的价格(P(T,T)=1)，满足以下随机微分方程:

(1)

S(t)为标的资产在t时刻的价格，满足以下随机微分方程：

(2)

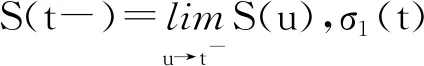
以下假设看涨期权和看跌期权具有相同的执行价格K和相同的到期日T。t0表示当前时刻，Tc表示选择时刻。c(t,S(t),T,K)和p(t,S(t),T,K)分别表示看涨期权和看跌期权在t时刻的价格，其中0≤t0≤t≤Tc≤T。由风险中性定价原理，选择期权在当前时刻的价格可以表示为

其中EQ[·|Ft0]表示条件期望。

引理1 随机微分方程(1)、(2)的解分别为

(3)

(4)

证明由It引理[10]可得结论。

(5)

将式(5)代入式(4)得到S(t)另一表达式

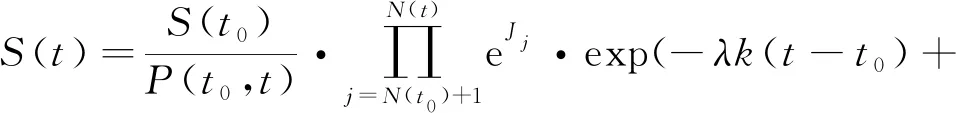
(6)

并且对于0≤u≤t≤T，有

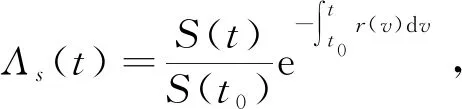
证明由式(4)，对任意的t0≤u≤t≤T,

(7)

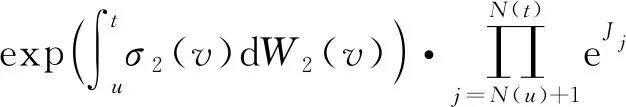
(8)

(9)

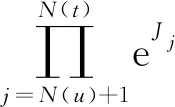
exp(λk(t-u))。

(10)

由式(7)—(10)得EQ[Λs(t)|Fu]=Λs(u)，所以{Λs(t)}是正Q-鞅过程。又EQ[Λs(T)]=Λs(t0)=1。引理3得证。

由引理2可定义概率测度QS，使得

(11)

(12)

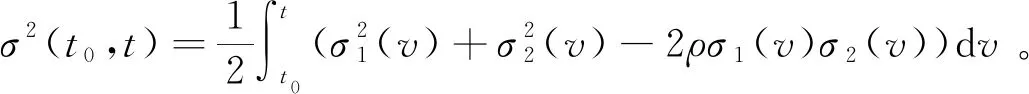
证明因为Yt关于Ft可测，所以由引理2及(11)式得

把式(5)、(6)代入整理得

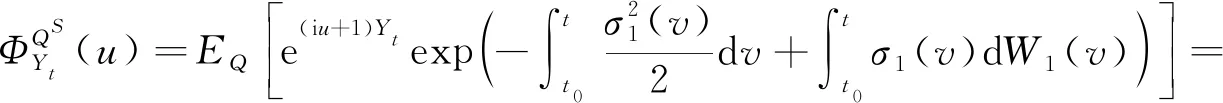
类似于引理3中式(8)—(10)的推导可得式(12)，引理4证毕。

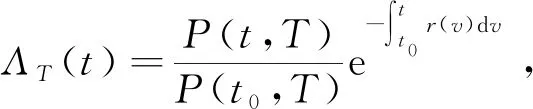
证明由式(3)，对任意的t0≤u≤t≤T，

类似于引理3证明可得EQ[ΛT(t)|Fu]=ΛT(u)，所以{Λs(t)}是正Q-鞅过程。又EQ[ΛT(T)]=ΛT(t0)=1。引理5得证。

由引理2可定义概率测度QT，使得

(13)

引理6 对于t0≤t≤T，Yt在QT下的特征函数为

(14)

其中σ2(t0,t)由引理4中给出。

证明因为Yt关于Ft可测，所以由引理2及式(13)得

把式(5)、(6)代入整理得

类似于引理3中式(8)—(10)的推导可得式(14)，引理6证毕。

引理7[11]若随机变量X在概率测度Q下的特征函数为ΦX(u)，则

2 主要结果

定理1当且仅当S(Tc)=KP(Tc,T)时，c(Tc,S(Tc),T,K)=p(Tc,S(Tc),T,K)。

证明由风险中性定价原理，

c(Tc,S(Tc),T,K)-p(Tc,S(Tc),T,K)=

(15)

最后一个等号是因为在风险中性测度Q下，资产的贴现价格为鞅。由式(15)可知结论成立。

定理2 选择期权在当前时刻t0的价格可由以下公式给出

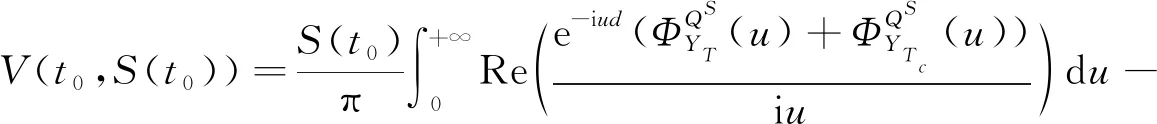
(16)

其中

t∈[Tc,T]。

证明由风险中性定价原理及定理1，选择期权在当前时刻t0的价格:

由引理2、式(11)及(13)，并注意到P(T,T)=1，可得

V(t0,S(t0))=S(t0)(EQS[I(S(T)>K,S(Tc)>KP(Tc,T))|Ft0]-EQS[I(S(T)

KP(t0,T)(EQT[I(S(T)>K,S(Tc)>KP(Tc,T))|Ft0]-EQT[I(S(T)

Yt与Ft0独立，所以

V(t0,S(t0))=S(t0)(EQS[I(YT>d,YTc>d)|Ft0]-EQS[I(YT

KP(t0,T)(EQT[I(YT>d,YTc>d)|Ft0]-EQT[I(YT

S(t0)(EQS[I(YT>d,YTc>d)]-EQS[I(YT

KP(t0,T)(EQT[I(YT>d,YTc>d)]-EQT[I(YT

根据示性函数I的性质，I(X1>a)-I(X1>a,X2>b)=I(X2

V(t0,S(t0))=S(t0)(EQS[I(YT>d)]-EQS[I(YTc

KP(t0,T)(EQT[I(YT>d)]-EQT[I(YTc

S(t0)(QS(YT>d)-QS(YTc

KP(t0,T)(QT(YT>d)-QT(YTc

由引理4、引理6和引理7可知定理2成立。

推论当J～N(θ,δ2)时，选择期权在当前时刻t0的价格仍由式(16)给出，其中

3 敏感性分析

本节考虑期权价格关于执行价格K、到期日T和选择时刻Tc的关系，取t0=0，S(t0)=2.5，P(t0,T)=0.9，σ1=0.1，σ2=0.2，λ=25，ρ=0.25，J～N(0.1，0.16)。

图1(a) 给出了当K=2、T=1时选择期权的价格与选择时刻Tc的关系，从图中可以看出，此种情形下，选择期权价格是Tc的严格单调递增函数。图1(b)给出了当K=2、Tc=0.05时选择期权的价格与到期日T的关系，从图中可以看出在此种情形下，选择期权价格是T的严格单调递增函数。图1(c)给出了当Tc=0.05、T=1时选择期权的价格与执行价格K的关系，通过观察可以看出，选择期权价格随着K的增大呈现出先减后增的变化趋势。

(a) 与Tc的关系 (b) 与T的关系 (c) 与K的关系图1 选择期权价格与Tc、T、K的关系

4 结论

假设贴现债券价格过程服从几何布朗运动，资产价格过程服从跳扩散过程。由于资产价格带跳，因此资产价格并不具有显式形式的密度函数。注意到随机变量的分布函数和特征函数具有一定的关系，因此考虑用特征函数的形式来表示衍生产品的价格。本文利用It引理和测度变换得到了当看涨期权和看跌期权具有相同到期日和相同执行价格时选择期权的价格公式，其形式相较于级数形式的结果更为简单。可以看出构造合适的等价鞅测度对于选择期权的定价是十分重要的，并且特征函数作为一种强有力的工具能够在一定程度上简化求解的过程。另外本文得到的定价公式扩展了文献[9]的结论，在资产价格过程跳跃的基础上加入了贴现债券价格随机，使所得结果更符合实际情形。