弱wakamatsu余倾斜模的若干注记

何东林

(陇南师范高等专科学校 数信学院， 甘肃 陇南 742500)

倾斜理论在Artin代数表示论和同调代数中扮演着重要的角色，许多学者对其进行了研究和推广[1-4]。特别地，Mantese等[5]介绍了wakamatsu倾斜模的定义，并讨论了其性质。何东林[6]引入n-余星模的概念，并研究了其与n-余倾斜模的关系。Bennis[7]为了讨论相对Gorenstein同调维数，给出了wakamatsu倾斜模和wakamatsu余倾斜模的一个推广，称之为弱wakamatsu倾斜模和弱wakamatsu余倾斜模。注意到n-余倾斜模与wakamatsu余倾斜模之间具有一定的联系，这样就会产生一个问题：n-余倾斜模与弱wakamatsu余倾斜模之间具有怎么样的关系？本文将给出这个问题的正面回答，并研究弱wakamatsu余倾斜模的等价刻画。

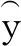
1 定义和引理

定义1[7]设C是左R-模。若存在HomR(ProdR(C),-)下正合的正合列

…→C1→C0→E0→E1→E2→…，

(1)

其中Ei是内射模，Ci∈ProdR(C)(i≥0)，且M≅Im(C0→E0)，则称M是GC-内射模。

定义2[7]设C是左R-模。如果满足如下条件：

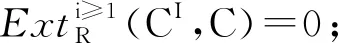
(2) 存在HomR(ProdR(C),-)下正合的正合列…→C2→C1→C0→Q→0，其中Ci∈ProdR(C)(i≥0)且Q是左R-模内射余生成子；

则称C是弱wakamatsu余倾斜模。

定义3[6]设C是左R-模。如果满足如下条件：

(1) idR(C)≤n(其中idR(C)表示C的内射维数)；

(3) 存在正合列0→Cs→…→C2→C1→C0→Q→0，其中Ci∈ProdR(C)(0≤i≤s)且Q是左R-模内射余生成子；

则称模C是n-余倾斜模。

证明设U、V∈ProdR(C)，则存在模M′和N′，以及集合I1和I2，使得U⊕M′≅CI1且V⊕N′≅CI2。因为对任意i≥1，有如下同构

引理2[7]设C、M是左R-模，则以下说法等价：

(1)M是GC-内射模；

(2)M∈ProdR(C)⊥且存在HomR(ProdR(C),-)下正合的正合列(ε):…→C2→C1→C0→M→0，其中Ci∈ProdR(C)(i≥0)。

引理3[7]设C是Π-self-orthogonal模，则GC-内射模的直积及直和因子是GC-内射模。

引理4[6]设C是左R-模，则以下条件等价：

(1)C是n-余倾斜模；

(2) Copresn(C)=⊥i≥1C，其中Copresn(C)表示由Cn-余表示的模类。

2 主要结论

定理1 对任意左R-模C，以下结论等价：

(1)C是弱wakamatsu余倾斜模；

(2)C是Π-self-orthogonal模，且每个内射余生成子均是GC-内射模；

(3)C是Π-self-orthogonal模，且每个内射模E均是GC-内射模。

证明(1)⟹(2) 设C是弱wakamatsu余倾斜模且Q为任意内射余生成子。由定义2知C是Π-self-orthogonal模，且存在HomR(ProdR(C),-)下正合的正合列

…→C2→C1→C0→Q→0，

(2)

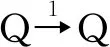
…→C2→C1→C0→Q→0→0→…，

(3)

显然Q≅Im(C0→Q)且正合列(3)在HomR(ProdR(C),-)下仍正合。由定义1知Q是GC-内射模。由Q的任意性可知，每个内射余生成子均是GC-内射模。

(2)⟹(3) 设C是Π-self-orthogonal模，且每个内射余生成子均是GC-内射模。对任意内射模E，都存在E′和集合I，使得E⊕E′≅QI。由引理3易得E是GC-内射模。

(3)⟹(1) 设C是Π-self-orthogonal模，且每个内射模E均是GC-内射模，则对任意内射余生成子Q，由于Q是内射模，所以Q是GC-内射模。从而存在HomR(ProdR(C),-)下正合的正合列

…→C1→C0→E0→E1→E2→…，

(4)

其中Ei是内射模，Ci∈ProdR(C)(i≥0)，且Q≅Im(C0→E0)。不妨考虑正合列

…→C2→C1→C0→Q→0，

(5)

由正合列(4)在HomR(ProdR(C),-)下正合可得，正合列(5)在HomR(ProdR(C),-)下也正合。根据定义2易知，C是弱wakamatsu余倾斜模。

下面讨论弱wakamatsu余倾斜模与n-余倾斜模之间的关系。

命题1 设模C是n-余倾斜模，Q是内射余生成子，则Q是GC-内射模。

证明由模C是n-余倾斜模及定义3可得，C是Π-self-orthogonal模，并且存在正合列

0→Cs→…→C2→C1→C0→Q→0，

(6)

其中Ci∈ProdR(C)且0≤i≤s。取Ij-1=Coker(Cj→Cj-1)(1≤j≤s)。对ProdRT中任意模P，用函子HomR(P,-)作用于短正合列0→Cs→Cs-1→Is-1→0，可得长正合列

(7)

对短正合列0→Is-1→Cs-2→Is-2→0，重复上面的过程，如此继续下去，易得正合列(6)在HomR(P,-)下正合。从而(6)在HomR(ProdR(C),-)下正合。易知M∈ProdR(C)⊥，正合列

…→0→0→Cs→…→C2→C1→C0→Q→0→0→…

(8)

在HomR(ProdR(C),-)下正合，且Q≅Im(C0→Q)。因此Q是GC-内射模。

定理2n-余倾斜模一定是弱wakamatsu余倾斜模。

证明设C是任意n-余倾斜模，根据定义3可得，C是Π-self-orthogonal模。由命题1知，对任意内射余生成子Q，都有Q是GC-内射模。又由定理1可得，C是弱wakamatsu余倾斜模。因此n-余倾斜模一定是弱wakamatsu余倾斜模。

推论1 设C是左R-模且Copresn(C)=⊥i≥1C，则C是弱wakamatsu余倾斜模。

命题2 设C是Π-self-orthogonal模且idR(C)≤n，则C是n-余倾斜模。

证明对任意基数λ，总存在以λ为基数的集合I。又由C是Π-self-orthogonal模可知，

(9)

0→Cs→…→C2→C1→C0→Q→0，

(10)

其中Ci∈ProdR(C)且0≤i≤s。注意到idR(C)≤n，从而C是n-余倾斜模。

定理3 设C是弱wakamatsu余倾斜模且idR(C)≤n，则C是n-余倾斜模。

证明设C是弱wakamatsu余倾斜模，则由定理1知C是Π-self-orthogonal模。又因为idR(C)≤n，根据命题2可得，C是n-余倾斜模。

下面用liD(R)表示环R的左内射整体维数。

定理4 设liD(R)≤n且C是左R-模，则C是n-余倾斜模当且仅当C是弱wakamatsu余倾斜模。

证明必要性 设C是n-余倾斜模，则由定理2可得C是弱wakamatsu余倾斜模。

0→Cs→…→C2→C1→C0→Q→0，

其中Ci∈ProdR(C)且0≤i≤s。又注意到liD(R)≤n，可见idR(C)≤n。因此C是n-余倾斜模。