多思维切入 妙方法破解——一道向量的最值题

黄光恩

(浙江省苍南县金乡高级中学 325805)

一、问题呈现

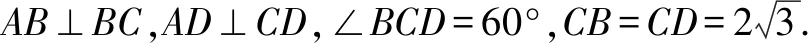
此题以平面四边形为问题背景，结合相关边上的动点的“动态”形式，进而来确定相应平面向量的数量积的最值问题.如何抓住动点的“动态”形式，转化为代数或图形特征的“静态”形式，这是破解问题的关键所在，也是主要的切入点.

二、三招破解

思维角度1(基底转化思维)

解法1(基底法1)

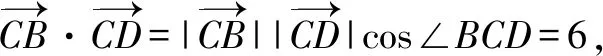
解法2(基底法2)

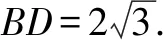
思维角度2(坐标运算思维)

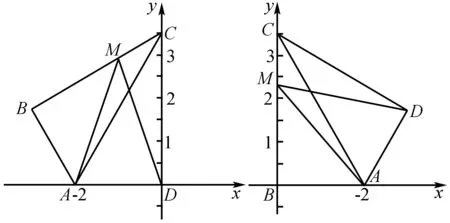
图1 图2

解法3(坐标法1)

解法4(坐标法2)

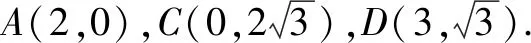
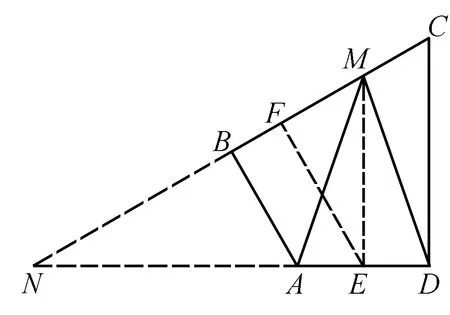
图3

思维角度3(极化恒等式应用思维)

解法5(极化恒等式法)

设AD的中点为E，过点E作EF⊥BC于点F.

三、规律总结

破解平面向量问题的常见技巧方法与策略多样，基底法是基本策略，借助平面向量的线性关系加以理清；坐标法是基本方法，借助建系把相关的点、平面向量用坐标形式加以表示；极化恒等式法是特殊形式，涉及数量积与平方关系时加以有效转化.无论哪种常用方法与常见技巧都要加以基本掌握，才能在具体求解问题过程中，以不变应万变，根据不同条件采取相应的方法来处理，从而真正提高数学能力，提升数学品质，培养数学核心素养.