高考备考中天体运动问题的常考题型与解析(上)

李红红

(河北省邯郸市第四中学 056107)

通过对2010-2019年全国卷高考物理试题的分析发现，每年都会对万有引力定律及其应用进行考查，尤其是以天体运动问题作为基本运动形式进行考查.除2010年全国Ⅰ卷和2012年大纲卷以计算题的形式出现在考题中以外，其他年份都是以选择题形式出现.所以在高考备考的过程中有针对性地对这部分知识进行复习，就能有效提高复习备考的效率.

复习目标

1.分析2010年-2019年10年全国卷高考真题，寻找考题中知识点的共性或规律；

2.归纳相关知识点的物理题型及关键思路；

3.提炼思维方法；

希望通过本专题的复习，学生能够对天体运动问题有一个清晰的知识网络、弥补知识上的漏洞、提高分析问题和解决问题的能力.

一、考题分析

表1

通过表1对高考真题考点的分析，可以发现高考题中所考查的知识点主要从两条线展开：其一是以天体A绕中心天体B作匀速圆周运动、万有引力提供向心力而设计的相关问题，如星球密度、双星系统、同步卫星、行星冲日(实则天体的追及问题)、宇宙速度以及延伸出来的变轨问题等；另一条线则是以在天体表面的物体随天体一起自转设计的相关问题，此条线展开的题中，需要自己根据题意判断是否考虑星球的自转问题；还有一类较为特殊的双星系统问题.纵观这10年天体运动的高考题还发现，从2017年开始，逐渐将天体运动与其他力学知识开始综合、对数学知识的要求也越来越高.比如：2019年第21题，以某两个未知星球为载体，创设平时力学知识的情境，而不是直接在地球表面去创设，使学生乍看此题时，感到一种陌生和不适应感，题中同时还设计了与图像的结合，大大增加了思考与选择的难度.

所以仔细分析考题发现：越来越多的考题将天体运动与其他板块物理知识(目前仍以牛顿定律、功与能等力学知识为主)进行综合考查.这也是在高考备考中必须要重视的一个命题趋势.

二、模型归纳

在高三的复习备考中，可以将天体运动归纳为以下几种单知识点模型，通过对单知识点的深入理解来提高解决综合问题的能力.

模型一环绕模型

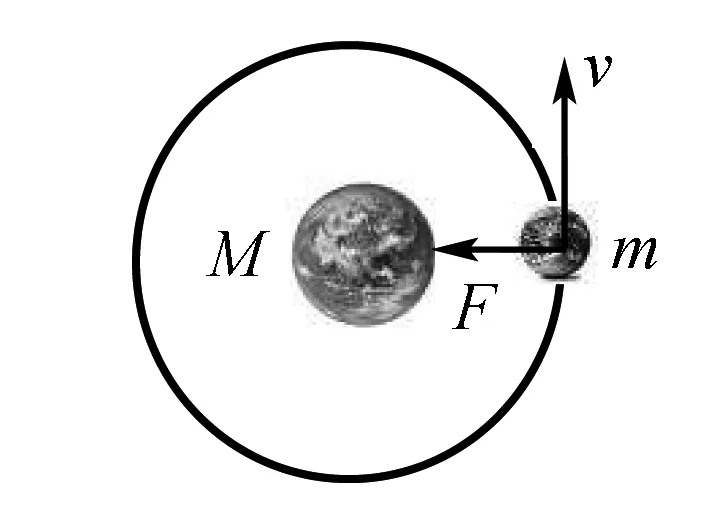
图1

基本规律：天体做匀速圆周运动，万有引力提供向心力；

题型一：计算星球的质量及密度

图2

此题型一般以某一未知质量或密度的天体M外有一颗环绕该天体运行的行星m或卫星m为情境，给出该环绕天体m的相关物理量(环绕半径r、线速度v、角速度ω、公转周期T等)，然后求该中心天体的质量或密度.

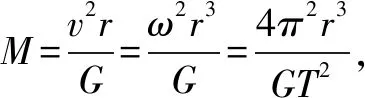
例1 嫦娥二号卫星开始绕月球做椭圆轨道运动,经过变轨、制动后,成为一颗绕月球作圆轨道运动的卫星.设卫星距月球表面的高度为h,作匀速圆周运动的周期为T.已知月球半径为R,引力常量为G.则下列选项正确的( ).

解析由万有引力提供向心力及密度公式，很容易计算出选项A、D是正确的.

题型二：比较行星或卫星的运行参量

此题型一般以某一中心天体M外有多颗环绕其运动的行星或卫星为情境，判断这多颗行星或卫星的运动参量的关系.

例2 (2018全国Ⅲ卷).为了探测引力波，“天琴计划”预计发射地球卫星P，其轨道半径约为地球半径的16倍；另一地球卫星Q的轨道半径约为地球半径的4倍，P与Q的周期之比约为( ).

A. 2∶1 B. 4∶1 C. 8∶1 D. 16∶1

解析设地球半径为R，根据题述，地球卫星P的轨道半径为16R，地球卫星Q的轨道半径为4R，由公转周期与轨道半径之间的关系，可得P与Q的周期之比为8∶1，选项C正确.

题型三：同步卫星

此题型依托同步卫星的公转周期与地球自转周期相等这一特点，延伸出“定轨道平面、定高度、定线速度”等一系列相关的物理情境进行考查.其解决问题的实质仍然是环绕模型的基本规律和基本公式，只不过同步卫星的一些运行参量是固定值，如：地球同步卫星的公转周期为T=24h，它与地面高度为h=35800km等等.

例3 (2016年课标卷Ⅰ).利用三颗位置适当的地球同步卫星，可使地球赤道上任意两点之间保持无线电通讯，目前地球同步卫星的轨道半径为地球半径的6.6倍，假设地球的自转周期变小，若仍仅用三颗同步卫星来实现上述目的，则地球自转周期的最小值约为( ).

A．1 h B．4 h C．8 h D．16 h

图3

解析地球自转周期变小，卫星要与地球保持同步，则卫星的公转周期也应随之变小，由环绕模型可知卫星离地球的高度也应变小，要实现三颗卫星覆盖全球的目的，则卫星周期最小时，就是三颗卫星的连线构成的等边三角形为地球这个圆形的外接三角形，如图3，然后由数学几何关系即可解得选项B正确.当然此题的难点就是做出最小周期时的卫星空间关系图，只有找到这层数学几何关系才能正确求解.

题型四：行星冲日

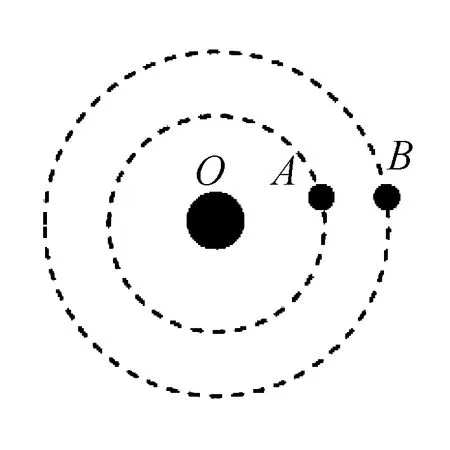
图4

“行星冲日”最早出现在2014年课标卷Ⅰ的高考题中，题中描述如下：当地球恰好运行到某地外行星和太阳之间，且三者几乎排成一条直线的现象，天文学称为“行星冲日”.可见“行星冲日”问题的本质仍然是环绕模型.

图5

此题型以围绕同一中心天体的两个或多个不同高度的天体为基础，研究这些不同高度的天体在运动过程中的特殊位置，如图4所示，A、B两星体处于与中心天体连线的半径的同一侧，此时两星体相距最近，反之，如果A、B两星体处于与中心天体连线的半径的两侧，此时两星体相距最远.这与直线运动中物体的追及相遇问题很类似.所以有时也把“行星冲日”问题看成是“卫星的追及相遇”问题.处理此类问题的关键要清楚了解：从两星体相距最近到下一次相距最近(或最远)满足的角度关系为：(ωA-ωB)t=2π(或(ωA-ωB)t=π).

例4 某行星和地球绕太阳公转的轨道均可视为圆．每过N年，该行星会运行到日地连线的延长线上，如图5所示．该行星与地球的公转半径比为( ).

题型五：变轨问题

此题型是在环绕模型的基础上进行了一些微变化，环绕模型中天体做稳定的匀速圆周运动，而此题型中天体所做的是一种动态变化的运动，即：天体可由原来低轨道的匀速圆周运动，通过在合适位置加速，变为椭圆运动，然后再通过合适位置加速，变为更高轨道的匀速圆周运动；反之由高轨道向低轨道变化也是如此.

在变轨运动中，如果天体作匀速圆周运动，则规律与环绕模型完全相同，如果天体作椭圆运动，则天体所受万有引力与向心力则不再相等，此时，如果环绕天体正远离中心天体，则是万有引力小于其所需要的向心力，即环绕天体作离心运动；如果环绕天体正靠近中心天体，则是万有引力大于其所需要的向心力，环绕天体作向心运动.

图6

例题5 (多选)如图6所示，发射同步卫星的一般程序：先让卫星进入一个近地的圆轨道，然后在P点变轨，进入椭圆形转移轨道(该椭圆轨道的近地点为近地圆轨道上的P，远地点为同步圆轨道上的Q)，到达远地点Q时再次变轨，进入同步轨道.设卫星在近地圆轨道上运行的速率为v1，在椭圆形转移轨道的近地点P点的速率为v2，沿转移轨道刚到达远地点Q时的速率为v3，在同步轨道上的速率为v4，三个轨道上运动的周期分别为T1、T2、T3，则下列说法正确的是( ).

A.在P点变轨时需要加速，Q点变轨时要减速；

B.在P点变轨时需要减速，Q点变轨时要加速；

C.T1

D.v2>v1>v4>v3

解析由题意可知，此变轨问题是由低轨道向高轨道变化，所以每个变轨位置均需要加速，这样其所受万有引力小于此处所需要的向心力，天体做离心运动，可知A、B两个选项均不正确；而由开普勒第三定律可知C选项正确；再由环绕模型中卫星运动参量的比较可知：v1>v4，而由低向高变轨时需要加速可知：v2>v1,v4>v3，所以选项D正确.答案为CD.(未完待续)