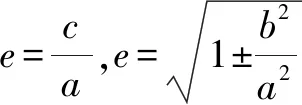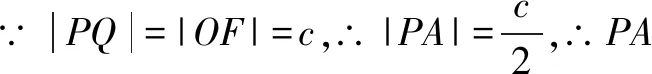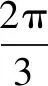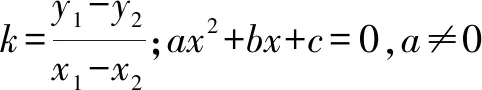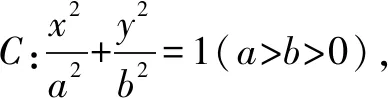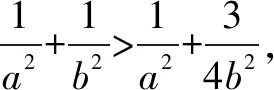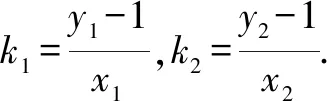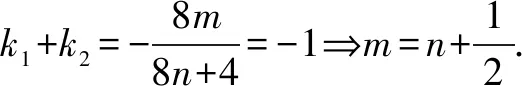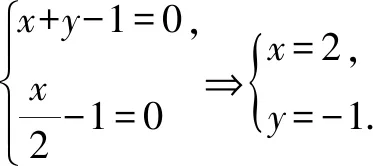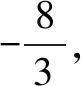齐次式的应用
张映雄
(云南省红河州蒙自市第一高级中学 661199)
齐次式在高中阶段是比较常见的一种结构,也是高考常考的一种结构.但是齐次式的用法比较零散,很多学生都是在解题过程中断断续续地学过用过,但是可能连自己都没意识到自己用的就是齐次式.本文将齐次式在高中阶段的用法做一些归纳整理,希望对各位读者有所启发.

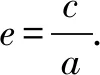
在实际应用中,齐次式经常会与三角公式、正弦定理、等比数列、不等式、函数、导数、离心率、斜率等知识相结合,形式多种多样.下面将列举一部分齐次式在高中数学中的应用.
一、齐次式在三角函数中的应用


解2sin2α=cos2α+1是隐藏的齐二次方程.

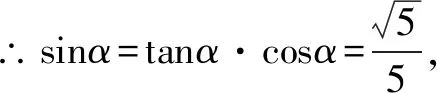
小试牛刀【2015广东 文】已知tanα=2.
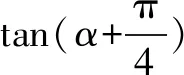
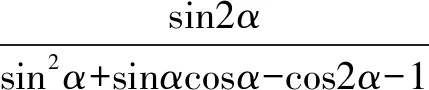
二、齐次式在解三角形中的应用

例2(2019年高考全国Ⅰ卷理数)△ABC的内角A,B,C的对边分别为a,b,c,设(sinB-sinC)2=sin2A-sinBsinC.
(1)求A;


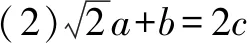
由于0° 小试牛刀(2018全国新课标Ⅰ文)△ABC的内角A,B,C的对边分别为a,b,c,已知bsinC+csinB=4asinBsinC,b2+c2-a2=8,则△ABC的面积为____. 小试牛刀(2012浙江)若正数x,y满足x+3y=5xy,则3x+4y的最小值是( ). 例4(2019年高考全国Ⅲ卷理数)已知各项均为正数的等比数列{an}的前4项和为15,且a5=3a3+4a1,则a3=( ). A.16 B.8 C.4 D.2 小试牛刀(2015年新课标2理科)等比数列{an}满足a1=3,a1+a3+a5=21,则a3+a5+a7=( ). A.21 B.42 C.63 D.84 当在出现二元变量时,若存在齐次式,可以通过乘除的方式,将二元变量降为一元变量,从而构造函数求解. 因为x>1时,f′(x)<0,所以函数f(x)在(1,+∞)上单调递减,故f(x) 因为x>1时,g′(x)>0,所以函数g(x)在(1,+∞)上单调递增,故g(x) (1)求实数a的值,并判断函数f(x)的单调性; (2)若函数f(x)=m有两个零点x1,x2,且x1 方法二:齐次式消元. 小试牛刀(2018届四川省广元市高第二次统考)已知函数f(x)=2lnx-x2+ax(a∈R). (1)当a=2时,求f(x)的图象在x=1处的切线方程; (1)求C的方程; (2)设直线l不经过P2点且与C相交于A,B两点,若直线P2A与直线P2B的斜率的和为-1,证明:l过定点. 解(1)由于P3,P4两点关于y轴对称,故由题设知C经过P3,P4两点. 牛刀小试(黑龙江省大庆市第一中学2019届高三下学期第四次模拟(最后一卷)考试数学试题)已知抛物线C:y2=2px(p>0)的焦点为F,直线y=4与y轴的交点为P,与抛物线C的交点为Q,且|QF|=2|PQ|. (1)求p的值;三、齐次式在均值不等式中的应用
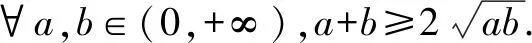
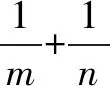
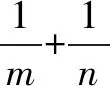
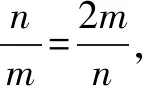
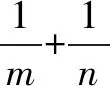
四、齐次式在等比数列中的应用

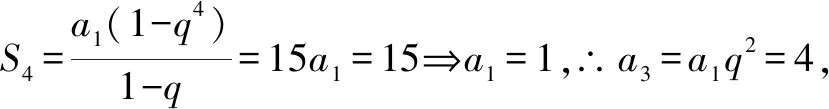
五、齐次式在导数中的应用



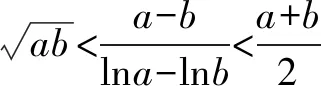
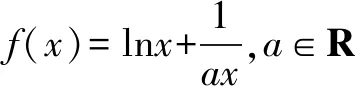
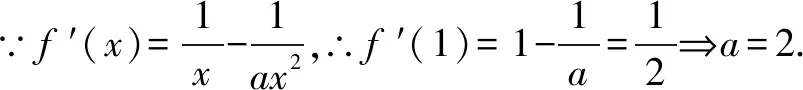
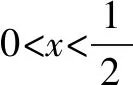


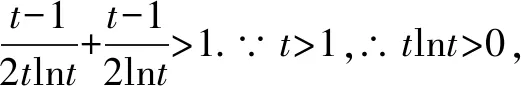
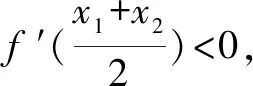
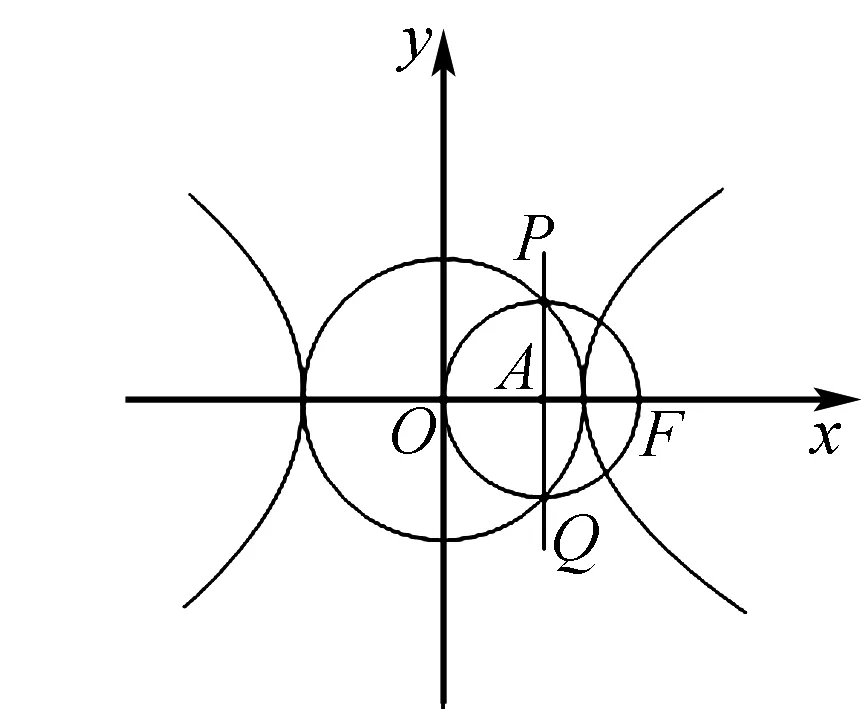
六、齐次式在圆锥曲线中的应用