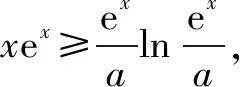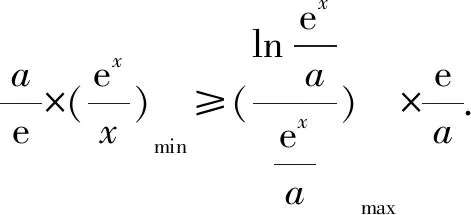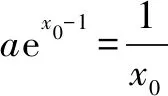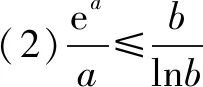2020年新高考全国Ⅰ卷(山东卷)数学第21题解法研究——同构放缩携起手导数不等式难题不再有

高振宁

(山东省新泰市第一中学 271200)

原题再现已知函数f(x)=aex-1-lnx+lna．

(1)当a=e时，求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积；

(2)若f(x)≥1，求a的取值范围．

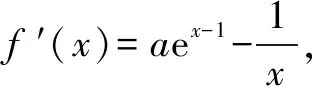
当a=1时，f′(1)=0,当x∈(0,1)，f′(x)<0，f(x)在(0,1)上是减函数;x∈(1,+)时，f′(x)>0，f(x)在(1,+)上是增函数.∴f(x)min=f(1)=1,故f(x)≥1恒成立.

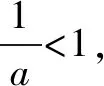
综上所述，实数a的取值范围是[1,+∞).

方法二(放缩法)：当0

当a>1时，f(x)=aex-1-lnx+lna≥ex-1-lnx，由a=1的结论可知f(x)=ex-1-lnx≥1恒成立.

综上可知：a的取值范围是[1,+).

方法四(同构函数y=xex):

因f(1)=a+lna≥1，设g(a)=a+lna，显然y=g(a)在区间(0,+)上是增函数，g(a)≥g(1)=1，故a≥1.f(x)=aex-1-lnx+lna≥1，得显然则原不等式等价于设g(x)=xex，显然g(x)在(0,+)上是增函数，则上述不等式等价于当时显然成立;当时，原不等式等价于由于ex≥1+x，且a≥1则可得故a的取值范围是[1,+).

方法六(分而治之法):

方法三、四、五可以归结成同构法，同构法的本质是构造目标函数，借助目标函数单调性把复杂函数简单化递减，比方说若F(x)≥0能等价变形为F(f(x))≥F(g(x))，若F(x)递增，则问题转化为f(x)≥g(x)，若F(x)递减，则问题转化为f(x)≤g(x).此类方法的关键是构造目标函数，高考压轴题中的构造常见形式可分为两类：

(1)aea≤blnb可以同构aea≤lnbelnb，借助函数f(x)=xex解决，也可以同构ealnea≤blnb，借助f(x)=xlnx解决，更可以同构为lna+a≤lnb+ln(lnb)，借助f(x)=x+lnx解决.

方法六属于解决问题的巧妙方法，不属于通性解法，一般情况下f(x)≥g(x)不等价于f(x)min≥g(x)max，但是对于极个别的问题，利用上分而治之的方法，会极大地降低运算程度，但是构造不等式两侧的目标函数有一定的技巧性，学生不易掌握.