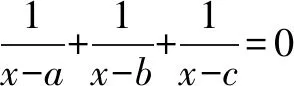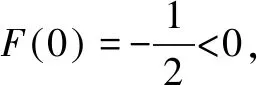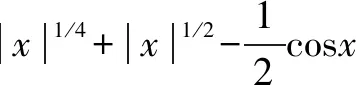利用连续函数性质讨论方程根的情况

张 盈

(陕西省西安市延安大学西安创新学院 710100)

一、预备知识

介质定理:设f(x)是闭区间[a,b]上的连续函数，且有f(a)=A，f(b)=B，则至少存在一点ξ∈(a,b)，使f(ξ)=C，其中C是介于A与B之间的一个数.

零点(或根值)定理：设f(x)是闭区间[a,b]上的连续函数，若f(a)·f(b)<0，则至少存在一点ξ∈(a,b)，使f(ξ)=0.

若存在x=x0，使方程f(x0)=0，则称x0是函数f(x)的零点. 函数的零点x0又称方程f(x)=0的实根.

证明方程存在实根有两层含义：一是在区间(a,b)内根的存在性；二是在区间(a,b)内根的唯一性.

二、用连续函数的性质讨论方程的根

1.证明方程根的存在性

解题思路：用连续函数的零点(或根值)定理.

(1)若题设给出方程，首先将方程写成F(x)=0的形式；然后，设函数F(x)，并验证该函数在所给的闭区间[a,b]上满足零点定理的条件，即可得到结论.

(2)若题目不是证明方程存在根，而是证明存在ξ∈[a,b](或x0∈[a,b])，使一含ξ的等式成立. 这时，先将欲证的含ξ的等式写成F(ξ)=0的形式，这相当于证明方程F(x)=0存在根ξ. 这只要作辅助函数F(x)即可.

(3)根值定理的推广：根值定理中的闭区间[a,b]，可推广到开区间，半开区间和无限区间.

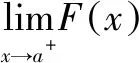
(4)根值定理是确定方程f(x)=0在开区间(a,b)内存在根. 若欲证方程f(x)=0在区间(a,b]，[a,b)和[a,b]上存在根，除用根值定理证明方程在(a,b)内存在根，对区间的端点还应加以讨论.

2.证明方程根的唯一性

解题思路：(1)先证方程F(x)=0在(a,b)内存在根，再验证函数F(x)在[a,b]上单调.

(2)反证法：设方程有两个根，而导出矛盾.

(3)证明f(ξ)=C.

证明函数f(x)在点x=ξ的函数值f(ξ)等于某一确定的常数C，即f(ξ)=C.常用证明方法有两种思路：

(1)用零点定理: 将f(ξ)=C写成f(ξ)-C=0，作辅助函数F(x)=f(x)-C. 只要证明方程F(x)=0存在根ξ即可.

(2)用介质定理：若f(x)在区间[a,b]上连续，且最大值与最小值分别为M和m，只要能证明常数C介于m与M之间，由连续函数的介质定理便得到欲证的结论.

例1设a

证已知方程可改写作

(x-b)(x-c)+(x-c)(x-a)+(x-a)(x-b)=0.

设f(x)=(x-b)(x-c)+(x-c)(x-a)+(x-a)(x-b)，因为f(x)在[a,b]上连续，且f(a)=(a-b)(a-c)>0，f(b)=(b-c)(b-a)<0，

所以由根值定理，存在ξ1∈(a,b)，使得f(ξ1)=0，ξ1是方程f(x)=0的根.

同理可证存在ξ2∈(b,c)，使得f(ξ2)=0，ξ2是方程f(x)=0的根.

先证根的存在性.

于是，由零点定理，在区间(0,1)内F(x)=0至少存在一个根.

注意到当x>1时，F(x)恒大于0，故在区间(1,+)内方程F(x)=0不可能有根.

例3设函数f(x)在[a,b]上连续，且a

例4试证方程x=asinx+b(a>0,b>0)至少有一个正根，且不超过a+b.

证本例即证方程在区间(0,a+b]上有根即可.

设函数F(x)=x-asinx-b，F(x)是初等函数，在闭区间[0,a+b]上连续. 由于

F(0)=-b<0，F(a+b)=a[1-sin(a+b)]≥0(a>0,sin(a+b)≤1).

若F(a+b)>0，则由零点定理知存在ξ∈(0,a+b)，使F(ξ)=0，即ξ=asinξ+b是方程的根.

若F(a+b)=0，则(a+b)为方程F(x)=0，即为方程x=asinx+b的正根.

综上，方程x=asinx+b至少有一个正根，且不超过a+b.