巧设曲线方程 提升运算效率

李怀忠

(甘肃省景泰县第二中学 730400)

一、巧用参数方程

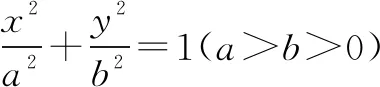
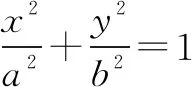
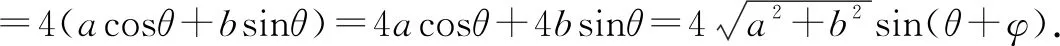
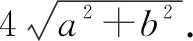
例2已知直线l：x+y-1=0与抛物线y=x2交于A，B两点，求线段AB的长和点M(-1,2)到A，B两点的距离之积.

点评参数方程把曲线上的点的横、纵坐标分别通过参数直接表达出来,比较清楚地指明了曲线上的点的坐标特征.对于圆锥曲线上与动点有关的最值，以及处理两线段长度的积、和、差等问题，有着普通方程无可比拟的优越性.

二、巧设曲线的模糊方程

分析曲线不明确焦点所在的位置，用标准形式求解需要分焦点在x轴和y轴上两种情况，相对而言计算比较麻烦.可采用模糊设法.

点评中心在原点，对称轴在坐标轴的椭圆、双曲线的一般方程都可设为Ax2+By2=1的形式，当题设条件中没有明显的几何量出现时，通常情况下使用模糊方程，它既可以避免分类讨论，又能简化运算.

三、巧设相交曲线系方程

例4已知圆x2+y2+x-6y+m=0与直线x+2y-3=0相交于P、Q两点，O为原点，且OP⊥OQ，求实数m的值.

分析本题常规解法是由OP⊥OQ得出等量关系，联立圆和直线方程组，借助韦达定理，构建关于m的方程求解，过程运算繁杂，可以考虑用直线和圆相交的曲线系方程.

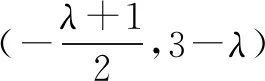
例5求过点A(2，1)和直线x-2y-3=0与2x-3y-2=0的交点的直线方程.

解所求直线过直线x-2y-3=0与2x-3y-2=0的交点，可设过两直线交点的直线系方程为x-2y-3+λ(2x-3y-2)=0.又因为过A(2，1)，所以代入得λ=-3.则所求方程为5x-7y-3=0.

点评在解析几何中我们常常会涉及到两圆锥曲线相交的相关问题，往往在处理这类问题时如按常规思路去解则运算量相对较大且不易算出来，相反如果利用好“曲线系”相关知识则可以大大简化解题过程中的运算量，事实上当两条曲线方程C1:f1(x,y)=0，C2:f2(x,y)=0，则过两条曲线交点的曲线系方程为f1(x,y)+λ[f2(x,y)]=0.

四、巧设特征曲线系方程

例6已知双曲线的一条渐近线方程为2x-3y=0且经过点(1,2)，求它的标准方程.

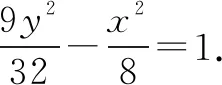
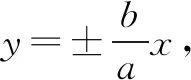
例7(2018·深圳一模)过点(3,2)且与椭圆3x2+8y2=24有相同焦点的椭圆方程为( ).

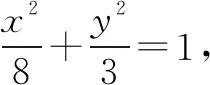
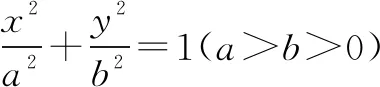
五、巧用极坐标方程

分析用直角坐标方程求定值，需要设A、B的坐标，对应的变量较多，化简繁杂，而且容易出错.认真分析题目信息，待证结论是与线段有关系的问题，选择极坐标更加直观、方便.

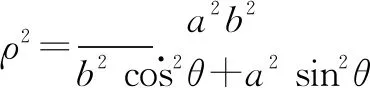
点评极坐标法是解决平面解析几何常用的方法，在解决过程中，遇到从一点出发的几条线段长度问题和角度问题常可以借助极坐标解决，利用极坐标的几何意义，结合三角函数可以使问题更加简洁、明晰.

教学实践表明，选择一个恰到好处的曲线方程就是成功的一半，一个好的方程不仅能简化运算，优化解题过程，同时也能深化学生的认知结构、拓展学生的思维能力，有效地提升课堂教学效率.因此，在平时教学中要引导学生总结解题经验，做好方法技能储备，解题前，多层次、多角度分析和思考，解题后进行全方位、多维度反思和评价，不断优化解题方法、深刻体验解题过程，促进知识融会贯通，不断提升学生解题能力和思维能力，形成完善的解题方法和策略.