基于经验视角 引之尝试『自渔』
——《角的度量》教学实践与思考(二)
王 笑
【教学内容】
苏教版四年级上册第79、80页。
【教学过程】
一、基于经验,操作中产生统一内需
1.回忆思辨。
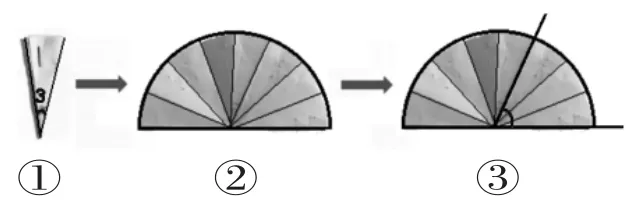
师:老师手里有两个角,∠A和∠B,(如下图①②)你能一眼看出哪个角大吗?

生:∠A 大,因为它的边更长。
生:角的大小不是看边的长短,这两个角张开的大小是差不多的,需要重合起来比一比才能知道哪个角大。
师:请你为大家展示一下比角的方法好吗?
生:将∠B 与∠A 的顶点和一条边重合,看另一条边,(如上图③)∠A 大。
2.操作比划。
师:∠A 到底有多大呢?我们可以借助学具篮中的角比一比。(如下图:学具篮中有两把三角尺及三个折成的小角。∠1 是60°、∠2 是30°、∠3 是22.5°)

(1)探究活动。
①拿一拿:从学具篮中拿出这些工具。
②比一比:同桌合作,用工具上的这些角去与∠A 比一比。
③说一说:同桌相互说一说∠A 有多大。
(2)交流反馈。
师:你们测量的结果是什么?
生:∠A 有一个∠1 那么大。
生:∠A 有两个∠2 那么大。
生:∠A 大约有三个∠3 那么大。
师:同样是测量∠A,结果为什么不同呢?
生:他们测量时用的工具不同。
生:我同意他的说法,但根据我们以往的学习经验,我认为要知道∠A 的大小,最好能统一测量工具,这样才能进行比较。
师:确实像这位同学所说,我们需要有一个统一的测量工具与方法,那就让我们一起来研究“角的度量”。(板书揭题)
【思考:“影响学习的唯一最重要因素,就是学习者已经知道了什么,要探明并据此进行教学。”此环节,通过“回忆思辨”,复习了二年级学习的角的初步认识;通过“操作比划”,感知∠A有一个∠1 那么大、有两个∠2那么大、大约有三个∠3 那么大,此时教师引导并提出了一个关键问题——“同样是测量∠A,结果为什么不同呢?”,由此引起认知冲突,产生了统一度量工具的内需。】
二、积累经验,交流中明晰度量原理
1.初步感知量角器的产生过程。
师:知道要用什么工具度量角的大小吗?
生:半圆形的量角器。
师:(边问边拆,如下图①②)同学们,这是学具篮里的∠3,老师将它打开,你认识吗?
生:认识,它就是“量角器”!
师:是的,这是一把“简易的量角器”,量角器其实就是由若干个角组成的。你能在量角器中找到角并说一说这个角有多大吗?
生:(上台指、说,如上图③)这有一个角,它有三个∠3 那么大。
(随后教师又请了三位学生到台前在这个简易量角器上找不同的角,并请同桌同学互相指、说)
【思考:初步感知量角器的产生过程,引导学生观察并到黑板前指出大小不一样的角,说一说这个角包含了几个∠3。充分感知量角器里有很多不同的角,不同的角都是由若干个相同单位的角组成的。】
2.自主探究量角器的简单构造。
师:那“精密的量角器”长什么样呢?看!(课件出示量角器)观察量角器,你看到了什么?
生:量角器上有很多刻度线,都指向量角器的中心。
生:量角器上面的数排成了两圈。
师:是的,里面这圈刻度我们称为内圈刻度,那外面这圈刻度叫什么呢?
生:外圈刻度。
师:量角器里藏了好多数学知识,请翻开教材第79 页,带着下面的思考,自学最后两段话。
(1)明确思考。
①说一说:角的计量单位是什么?
②想一想:量角器上的1°角在哪里?量角器中有多少个1°角?
③找一找:从右边起,找出0°、20°、90°、135°、180°刻度线;再从左边起,找出0°、20°、90°、135°、180°刻度线。
(2)交流反馈。
生:度是角的计量单位,用符号“°”表示,1 度记作1°。(板书)
生:这两条刻度线延长到中心就形成了1°角。
生:将这两条刻度线延长到中心形成的角,度数也是1°。(如下图)

生:每两个相邻刻度间所对的角都是1°。
生:老师,我发现量角器中有180 个1°角。
师:你从哪里看出来的?
(学生到台前指一指)
生:老师,我还知道这是左边的0°刻度线、这是右边的0°刻度线……(边指边说)
3.思维迁移读整十度的角。
师:同学们了解了量角器,你会使用它吗?那我们课前研究的这个∠A 到底有多少度呢?谁能用大屏上的量角器量一量?
生:(如下图,学生边摆边说)将角的顶点与中心重合,一条边与右边0°刻度线重合,摆好后,我发现∠A 里有6 个10°角,所以∠A 是60°。

生:我认为角的一条边与左边0°刻度线重合也可以。
生:他们的方法都是可以的,但不用去数6 个10°角是60°,直接看它的另一条边就可以了,另一条边指着数字60,那就是60°。
生:我有疑问。另一条边所在的地方,有60°和120°两个度数,怎么确定是60°呢?
师:这个问题我觉得很有意思,谁能解答呢?
生:∠A 是个锐角,比直角小,所以不可能是120°。
生:其实∠A,它的起始边与内圈0°刻度线重合,就读内圈刻度60°。
生:我们只要看角的一条边,与内圈的0°刻度线重合,就读内圈刻度;与外圈的0°刻度线重合,就读外圈刻度,所以读出来都是60°。
【思考:学生的思维能力在经验迁移中能得到很大的提升。在上一层次中,学生已经充分感知“量角器中不同的角都是由若干个相同单位的角组成的”,这一环节,学生在度量实物∠A 时,就很自然地说出“∠A 里有6 个10°的角,所以是60°”。学生走向台前,大胆表达读角的方法,生生互相补充,进行方法优化。】
4.认知提升读非整十度的角。
师:(拿起实物∠B)同学们,看这个角,你也会像刚才一样量一量它是多少度吗?
生:这个角比40°大一些。(如下图,学生上台拿∠B 与课件中的量角器比对)

师:能准确地读出∠B 的度数吗?
生:(指着内圈,一度一度地数)40°、41°、42°、43°、44°、45°。∠B 是45°。
生:我要补充。我和他结论一样,但我不用一度一度地数,5°刻度线稍微长一些,所以一眼就能看出是45°。
【思考:教育家波利亚提出“学习任何新知的最佳途径是由学生自己去发现,因为这种发现理解最深,也最容易掌握内在的规律和联系”。此环节,学生拿着∠A 去比对,比的过程中就学会了量角、读角的方法;再拿着∠B去比对,发现不是整十度的角,于是自然产生“40°、41°、42°、43°、44°、45°”这样一度一度地数的情况,这是学生解决认知冲突的需要,这样的内在知识才会被理解得更深。】
三、发展经验,活动中深探度量本质
1.尝试操作。
师:度量画在纸上的角,不能拿到量角器上去比怎么办?(如下图,教师出示75°的∠C 与130°的∠D)
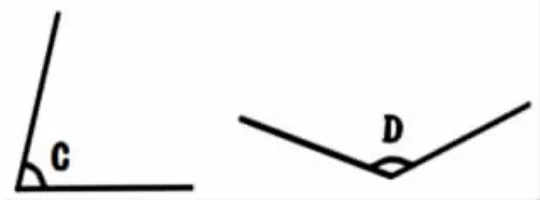
生:我们可以拿量角器到角上去比一比。
师:那行,请同学们动手试一试吧!
(学生尝试操作,教师巡视,然后教师呈现学生动态操作过程的视频)
2.资源呈现。
(交流呈现两种动态视频:第一种,度量∠C,完全正确;第二种,度量∠D,错误资源)
师:先请度量∠D 的学生代表说一说是怎么操作的,其他学生倾听并补充。
生:量角器的中心和角的顶点重合,内圈的0°刻度线和一条边重合,看另一条边,所以∠C 是75°,有需要补充的吗?
生:我同意你的观点,另一条边对应两个刻度,分别是75°和105°,你应该强调一下,一条边和内圈的0°刻度线重合,要读内圈刻度,所以是75°。
师:认真倾听是对别人的尊重,倾听后的补充使得度量的方法更加完整。
师:再来看看第二个视频,你有话要说吗?
生:∠D 的一条边不在水平方向,我们可以转一下纸,使得一条边在水平方向。
生:是的,我同意他的观点。当然也可以将量角器稍微转一转,使得0°刻度线与∠D 的一条边重合。
师:刚才量错的同学,请再动手试一试!
【思考:“动手操作的过程,不仅是一个实践的过程,更是尝试、想象、推理和反思的过程。”两种资源的捕捉,先呈现第一种,以生教生;然后呈现第二种,学生能及时发现自己的问题所在并纠正。动手操作,通过尝试及反思,学生不仅学会了如何度量,还掌握了知识间的联系,从拿着实物角到量角器上去比,发展到用量角器去量纸上的角。在此过程中,教师只是引导者,真正方法的获得全部来自于学生自己经验的发展。】
四、积累经验,说明中发散度量思维
师:通过今天的学习,你有哪些收获?我们是怎么探究的?
师:课后请你为量角器写一份使用说明书。
——《角的度量》教学

