细雨润物 让思维“生长”
——学本课堂中培养高阶思维的尝试
赵薇萍
数学被称为“思维的体操”,在数学教学中对学生的思维训练是必不可少的。思维能力的训练是一种有目的、有计划、有系统的教育活动。思维训练的主要目的是改善思维品质,提高学生的思维能力。优秀的思维品质主要包括深刻性、灵活性、独创性、批判性、敏捷性和系统性等几个方面。本文就其中的四个方面谈谈教学中的几点尝试。
一、纵横勾连,培养思维的系统性
系统性是指思维活动的有序程度,以及整合各类不同信息的能力。数学是门系统性很强的学科。教学时,应引导学生站在系统的高度学习知识,注重知识的整体结构,经常整理归纳知识。寻找新旧知识的联系与区别,挖掘共性,分离个性,在比较中学习新知识。注重知识的纵横联系,在融会贯通中提炼知识,领悟其关键、核心和本质。
1.立足基础,知晓原理。
数学的概念、性质、定理、公式的得出都有严格的推理论证。教学中,要引导学生在探究新知的过程中理解算理,了解来龙去脉,做到知其然并知其所以然。比如,四年级学习乘法分配律,这是重点,也是难点。课本中通过种树情境来引入,定律的得出依托于具体事例,再通过几个式子的计算验证得出定律。教师可以通过乘法意义这个算理来帮助学生进一步理解,如35×3+35×7,理解成3 个35 加7 个35 等于10 个35,写成35×(3+7)计算比较简便,也就是把相同加数的个数先合起来再乘相同加数。笔者用这样的图示来助推学生对乘法分配律的理解。
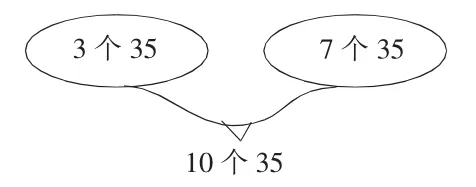
抽离具体情境从算理层面分析学生就不会生搬硬套定律了。把乘法意义和运算定律联系起来,使前后知识产生无缝对接。
学习数学知识时要引导学生立足基础,追本溯源,知晓原理,这是培养思维系统性的起点。
2.纵横勾连,触类旁通。
每学习一个知识点,都要让学生知道前因后果,明白知识从哪里来,到哪里去。比如第一学段学习整数加法的计算方法,学生知道了要相同数位上的数相加就是把计数单位的个数相加,接着学习小数加法和分数加法时,教师也要讲清算理,让学生知道,小数点对齐就是把相同数位对齐了再加;分数相加,分母相同的情况下,分母不变,分子相加,都是计数单位的累加,知识之间是相通的(如图)。

把教材中貌似分离的小数加法、分数加法和整数加法连接起来,沟通了知识之间的联系,共同纳入到加法体系中,完善了学生的知识结构,有利于培养思维的系统性。
注重知识之间的相互渗透和迁移,只有知识形成体系后,才能真正被消化和吸收。比如三年级学习排列和组合,课上主要通过列举法让学生知道有序思考,才能不重不漏。课本中例1 是“用0、1、3、5 能组成多少个没有重复数字的两位数”。课后有不少习题,学生基本都能轻松完成,可面对下面一题时,不少学生却一筹莫展。

笔者在课上启发道:“我们可以把四个垃圾桶编上号,想一想,“其他垃圾”桶位置有限制,编几号呢?”学习能力强的学生马上联想到,“‘其他垃圾’桶不能放到最左边”相当于0 不能放在最高位,“其他垃圾”桶编0 号,把另外三个垃圾桶编上1、2、3 号,就像用0、1、2、3 排四位数一样排它们的位置。随着学生的回答,笔者在黑板上写下了“其他垃圾0,厨余垃圾1,可回收物2,有害垃圾3。”“现在如果请你用0、1、2、3 排四位数,你会吗?”“会。”学生恍然大悟。有些学生的系统思维能力本身比较强,只要教师稍加启发,就能给其他学生起到导向作用。“那生活中还有什么事可以这样想呢?”笔者乘胜追击,希望借此促进“排列”这个知识体系的形成。
考虑问题,要从整体出发,处理好整体与局部的关系。学习新知的同时不忘沟通联系旧知,使学生的知识结构具有序列性、系统性。
二、巧妙变通,培养思维的灵活性
灵活性是指思维活动的灵活程度。它的特点包括:一是思维起点灵活,即从不同角度、方向、方面思考,能用多种方法来解决问题;二是思维过程灵活,从分析到综合,从综合到分析,全面而灵活地进行“综合分析”;三是概括迁移能力强,运用规律的自觉性高;四是善于组合分析,伸缩性大;五是思维的结果往往是多种合理而灵活的结论。灵活性反映了智力的“迁移”,如我们平时说的“举一反三”“运用自如”等。灵活性强的人,善于从不同的角度与方面进行思考,能较全面地分析、思考问题和解决问题。
1.一题多解,发散思维。
发散思维是指大脑在思维时呈现的一种扩散状态的思维模式,一题多解是培养发散思维能力的有效方法。课本中有很多可以一题多解的题目。如三年级学习长方形面积后有这样一道题,笔者指导学生就怎样求面积展开了讨论。受当时掌握知识所限,学生想出了五种方法,如果掌握知识多一些,方法更多。两个长8 厘米、宽3 厘米的长方形拼成的图形,面积是多少?如下图。

解法一:8×3×2-3×3
解法二:(8-3)×3+8×3
解法三:8×8-(8-3)×(8-3)
解法四:(8-3)×3×2+3×3
解法五:(8-3+8)×3
这几种方法从不同角度去思考,体现了思维的灵活性。解决一个问题,往往有多种途径。教师要抓住这种可一题多解的问题,组织好课堂讨论,让学生畅所欲言,相互启发,培养学生的发散思维能力。
2.对比优化,巧妙变通。
学习过程中,我们要引导学生多维思考,善于变通,灵活解决问题。在得出解决问题的多种方法后,可以把不同方法加以对比,进行优化。
如下题,可组织学生讨论,用什么方法可以很快知道哪位老师打字更快?
王老师4 分钟打了385 个字,李老师5 分钟打了512 个字。哪位老师打字打得更快?
学生有的通过计算385÷4,512÷5;有的通过估算385÷4≈400÷4=100,估大了,实际小于100,512÷5≈500÷5=100,估小了,实际大于100,所以李老师快。还有学生说,385÷4 商是两位数,512÷5 商是三位数,所以李老师快。这三种方法,一种比一种灵活。
三、敢于质疑,培养思维的批判性
批判性是指思维活动中独立发现和批判的程度。思维的批判性品质,来自于对思维活动各个环节、各个方面进行调整、校正的自我意识。它具有分析性、策略性、全面性、独立性和正确性等五个特点。
1.讨论辨析,自我修正。
数学是门逻辑性很强的学科,思考表达都要精准严密,不能以偏概全,不能有丝毫纰漏。课本中有些描述性的话一定要严谨,在学生初步得出结论后,我们要引导学生进行推敲。比如,学习和0 有关的除法时,经过0÷2=0,0÷8=0……这样几道习题的计算,学生很快得出结论:“0 除以任何数都得0。”学生已经知道了“任何数乘0 都得0”,再加上这几道习题,所以这个结论是顺其自然得到的。不仔细推敲,似乎是正确的。在大家都觉得这个结论正确的情况下,笔者出示,“0÷0=( )”,这下教室里热闹了,有的说,等于0,有的根据做除法想乘法的方法,说有无数种可能。经过思考,学生说,不确定。“那你们能自己把这个结论修改正确吗?”讨论到这儿,正确结论“0除以任何不是0 的数,都得0”已是呼之欲出。
还可以通过判断题来提高思维的批判性。如学习分数的意义后,可以通过这样的题让学生判断:“有两根同样长的绳子,一根减去了四分之三米,另一根减去了四分之三,两根绳剩下的长度相等。”这道题思维含量很高,可以大做文章。针对学生判断的两种情况,教师可以让认为对的或错的都各自说出理由,再举例说明什么情况下第一根长,什么情况下第二根长,什么情况下两根一样长。
在知识易混淆处或概念模糊时,我们要引导学生展开讨论,辩一辩、理一理,自我改正错误,得出正确结论。
2.大胆质疑,挑战权威。
学起于思,思源于疑。我们还要培养学生大胆质疑的学习态度。比如三年级学习了周长和面积之后,我看到一本书上有这样一道拓展题:“用64 米长的竹篱笆,利用一面墙围成一个养鸡场。如果每条边的长度都是整米数,怎样围才能使养鸡场的面积尽可能大呢?”书上的答案是这样的:

不仔细思考,这个答案很完美,在周长相等的情况下,长和宽越接近,面积越大。真的是这样吗?我启发学生通过画图来探究是否还有其他可能性。学生通过进一步探究发现还有面积更大的。请看下面图示。
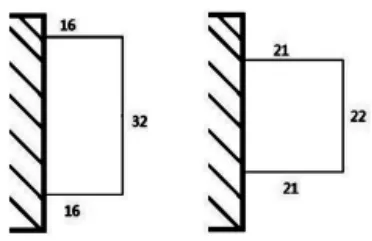
32×16=512(平方米)
21×22=462(平方米)
512>462
原来当一边靠墙,两条宽加起来和长相等时,面积才是最大的。
我们要用批判的眼光来看待问题,多问几个“为什么”,善于发现问题和提出问题,解决问题时一定要独立思考,考虑周全。
四、标新立异,培养思维的独创性
独创性即思维活动的创造性。在实践中,除善于发现问题、思考问题外,更重要的是要创造性地解决问题。独创性源于主体对知识经验或思维材料高度概括后集中而系统的迁移,进行新颖的组合分析,找出新异的层次和交结点。概括性越高,知识系统性越强,伸缩性越大,迁移性越灵活,注意力越集中,则独创性就越突出。
1.推陈出新,大胆尝试。
要培养学生的创新能力,教师首先要有创新精神,敢于对课本中的留白部分做出自己的决策。如三年级学习《年、月、日》时,课后习题中有保质期的推算,课本中没有规范的表示范例,要想书面表达清楚有点麻烦,怎么办?笔者指导学生用图示法。以作业本中一道习题为例,2019年3月1日的早晨,几号的牛奶还能喝?思考过程:2019年是平年,二月是28 天,牛奶2月24日生产,经过7天保质期,保质到3月2日。表示方法一:28-24+1=5(天),7-5=2(天)。所以3月1日早晨24 号牛奶还能喝。表示方法二:2月24日保质7 天,到3月2日,显然第二种方法更简洁明了。
2.独辟蹊径,标新立异。
有些学生很有自己的想法,不走寻常路,敢于提出不同意见。对于这些“另类”的学生,我们要呵护有加。比如用连乘解决问题,超市一周卖出5 箱杯子,每箱12 个,每个45 元,一共卖了多少钱?
课本呈现两种解法:
解法一:45×12×5,先算每箱卖了多少钱,再算一共卖了多少钱。
解法二:12×5×45,先算每箱共有多少个保温杯,再算一共卖了多少钱。
还有第三种解法吗?课本中没有提到。
如果有学生列出的算式是45×5×12,你认为对吗?不仔细想,似乎是没道理的,因为5 箱和每个45 元这两个信息间没有直接的联系。但是当有学生能自圆其说,把这个算式解释通,你还认为这没道理吗?学生说,假设每箱只有一个杯子,5 箱能卖45×5元,实际每箱有12 个,是假设的12 倍,再乘12。这么一假设,还挺有道理。所以只要能说清算理,都可以算对。课本例题没出现这种方法,我们也可以让学生用。教师要鼓励学生多思考,敢为人先。我们要以开放的、包容的心态去接纳学生的奇思妙想。
综上所述,引导学生探究知识的过程中,教师要做个有心人,指导学生在务实的基础上纵横勾连所学知识,构建起知识体系,学会巧妙变通,敢于批判质疑,勇于标新立异,力求通过日常教学活动使学生成为具有高阶思维能力和富有创新精神的新型人才。

