进化状态判定与学习策略协同更新的二进制粒子群优化算法

李浩君，何佳乐，聂新邦，杨 琳

(浙江工业大学 教育科学与技术学院，浙江 杭州 310023)

粒子群优化算法(PSO)是一种模拟鸟类群体社会行为的智能搜索算法[1]，通过群体内个体之间的信息共享对问题的解进行协同搜索。该算法除了具有结构简单、控制参数少、全局寻优能力突出等优点，还具备计算速度快、参数较少、实现方便等特点[2]，自提出以来便引起了国内外学者的广泛关注，在不同领域都得到快速广泛的应用。但是该算法在搜索过程中存在过早收敛或陷入局部极优的问题，因此需要对PSO算法进行优化研究。对粒子群算法的优化，最初都是通过对速度、位置更新公式中的参数进行修改，以达到算法优化的目的，如：Zhang等[3]通过在标准粒子群速度更新公式中引入活跃目标点，提出了具有新学习目标点的粒子群优化算法(APSO)，种群在进化过程中，构成了基于三目标点的速度迭代机制，使个体同时向三个优化位置学习。由于不同的算法优化的强度不同，可以学习或结合其使用的策略来进行优化与改进。Liang等[4]提出三种学习策略的粒子群算法：精英粒子群算法(ELPSO)、多标榜学习粒子群算法(MELPSO)和全面学习粒子群算法(CLPSO)，每种算法使种群中每个粒子向其余不同粒子的历史最优位置的不同维数学习，随机进行独立升级，保证了种群收敛过程中的多样性；刘衍民等[5]提出一种基于自适应动态邻居广义学习粒子群算法(ADPSO)，使种群粒子向全局、自身和邻域最优粒子学习，并在新产生的粒子位置上添加随机位置以增加粒子跳出局部最优区域的概率；高颍丽等[6]提出了一种融合分类优化与拓展策略的粒子群优化算法，采取一种正态演化变异策略，搜索当前最优粒子的邻域空间，增强局部开采能力以避免算法陷入局部最优；何通能等[7]设计了一种改进型粒子群算法，通过引入遗传算法中的交叉变异策略来增强算法收敛速度和精度得到近似最优解，提高算法优化的准确性。

除了考虑单个粒子的优化，学者针对全局粒子以及邻域内的其他粒子的影响因素对粒子群算法进行了优化。Peram等[8]提出了一种基于适应度值与粒子距离之比的粒子群优化算法(FDRPSO)，算法选择当前邻域中适应度值之差与粒子距离比值最大的个体作为种群新的全局学习目标nbest，使整个种群同时向pbest，gbest和nbest学习，从而增加种群多样性，提高了寻优性能；Mendes等[9]认为在进化过程中种群个体行为并非仅受某个特定粒子个体的影响，而是会受其所有邻域中的个体最优点影响，并根据该理论提出了全信息粒子群优化算法(FIPSO)，改善了整个种群的学习能力；Zhan等[10]提出了一种正交学习粒子群算法(OLPSO)，通过正交试验设计来寻求粒子个体的历史最佳位置和邻域最佳位置的最优组合，引导粒子更加快速地稳定，向全局最优位置靠近；董辉等[11]在传统的粒子群算法中引入小生境思想对各子群进行单独优化，并取出最好粒子形成新群体，再运用蛙跳算法进行优化；彭建新等[12]提出了一种基于全局信息的改进粒子群优化算法，采用所有粒子的历史最优平均值作为引导个体飞行速度的一个因素，形成全局信息，增强了种群的多样性。PSO算法存在早熟、易陷入局部最优的问题，其主要原因是在优化过程中种群丧失多样性。保持种群多样性是增强算法全局搜索能力、避免出现早熟现象的重要措施，因此笔者在粒子群优化算法迭代过程中采用基于进化状态信息判定的学习策略更新机制，提出一种进化状态判定与学习策略协同更新的二进制粒子群优化算法。进化状态判定的收敛阶段采用全信息学习策略，粒子i速度和位置的更新受适应度值更优邻域粒子的影响，提高了收敛速度；进化状态判定的跳出局部最优阶段采用局部信息学习策略，维持种群多样性避免算法陷入局部最优。

1 进化状态判定与学习策略协同更新的二进制粒子群优化算法

与传统粒子群算法不同，改进算法利用种群进化状态信息选择合适的学习策略。当进化状态大于固定阈值时，判定算法处于收敛阶段，采用全信息学习策略，依据更优邻域粒子的信息更新速度和位置，以加快算法收敛速度；当进化状态小于固定阈值时，判定算法处于跳出局部最优阶段，算法采用局部信息学习策略，依据局部最优和最佳邻域粒子的信息更新速度和位置，以维持种群多样性，使算法不易陷入局部最优。

1.1 进化状态分析

利用进化状态可以有效提高算法的性能[13-14]。种群多样性减少是粒子群算法陷入局部最优的主要原因，针对这一特性和迭代次数与种群多样性的线性关系定义进化因子E，其计算式为

(1)

(2)

(3)

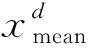
1.2 邻域选择策略

迭代过程中，针对二进制粒子群算法编码特性计算各粒子与其他粒子的海明距离，并对其进行排序，依据排序结果求出给定粒子指定个数的邻居。

Dij=H(xi,xj)j=1，…，N;j≠i

(4)

S=sort(D)

(5)

Neighbors=S(1∶T)

(6)

式中：Dij表示第i个粒子与种群中第j个粒子之间的海明距离；H为计算海明距离的函数；S为对排序结果的集合；Neighbors表示当前邻域粒子；T为指定邻居数量。

1.3 全信息学习策略

全信息粒子群算法(FIPSO)具有较快的收敛速度，但在算法后期容易陷入局部最优[9，15]。为更好地解决离散问题，在BPSO的基础上采用全信息学习策略以保证算法的寻优能力和收敛性能。算法迭代过程中，粒子i从适应度值更优的邻域粒子处获取信息，同时避免受不良邻域粒子的影响，适应度值越优的邻域粒子对粒子i的影响越大[16]。基于以上思想，ELBPSO采用全信息学习策略，其速度与位置更新表达式为

(7)

(8)

(9)

依据相关文献，采用收敛系数X和加速度系数φ调节粒子速度，算法性能较佳[9,17]，其中X=0.729，φ=4.1；ki为粒子i更优邻域粒子的个数；im为粒子i的第m个更优邻域粒子；pim为粒子im的位置，f(pim)为的适应度值，sumi为更优邻域粒子适应度值的总和；rm表示均匀分布于[0,1]之间的数。

1.4 局部信息学习策略

采用局部信息学习策略可以很好地维持种群多样性[17-18]。粒子i依据局部最优和最佳邻域粒子的信息更新速度和位置，受其他粒子的影响较小，可以在搜索空间更加自由地移动，有利于维持种群多样性。ELBPSO采用局部信息学习策略其速度与位置更新的表达式为

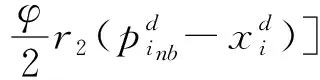
(10)

式中：pi为粒子i的局部最优位置；pinb为粒子i邻域的最优位置；r1和r2表示均匀分布于[0,1]之间的数。

1.5 进化状态判定与学习策略协同更新的二进制粒子群优化算法

理想的粒子群算法应当在保证较快收敛速度的同时不易陷入局部最优，采用单一学习策略很难实现这种状态，因此笔者提出一种进化状态判定与学习策略协同更新的二进制粒子群优化算法，在不同的进化状态下采用不同的学习策略来解决复杂的最优化问题。Zhan等[19]将种群迭代过程的进化状态分类为收敛、探索、开发、跳出局部最优4 个阶段，并以进化因子0.7为界点对跳出局部最优阶段进行区分。针对粒子群算法存在早熟、易陷入局部最优的问题，将粒子群迭代过程分为跳出局部最优和收敛两个阶段。Zhan等[19]同时对进化状态进行划分，若进化因子E<0.7，判定算法处于跳出局部最优阶段，表明种群多样性较差，应选择局部信息学习策略，保证粒子可以在搜索空间更加自由地移动，以维持种群多样性；若进化因子E>0.7或E=0.7，判定算法处于收敛阶段，表明种群多样性较好，应选择全信息学习策略，保证粒子从适应度值更优的邻域粒子处获取信息以加速收敛。改进算法的步骤为

步骤1种群初始化。种群规模设置为20，学习因子均固定为2，迭代次数300，维度300。

步骤2进化状态判定。计算进化因子E，若E<0.7，则判定算法处于跳出局部最优阶段；若E≥0.7，则判定算法处于收敛阶段。

步骤3粒子速度更新。若算法处于跳出局部最优阶段，采用式(10)更新粒子速度；若算法处于收敛阶段，采用式(7，8)更新粒子速度。

步骤4粒子位置更新。采用式(9)更新粒子位置。

步骤5重复步骤2～5，直到满足终止条件。

步骤6满足终止条件(达到最大迭代次数)，输出最优值并求出相应目标函数值，算法结束。

ELBPSO算法中进化状态判定是平衡收敛与跳出局部最优的关键，进化状态判定与学习策略协同更新的二进制粒子群优化算法的优化机制如图1所示。

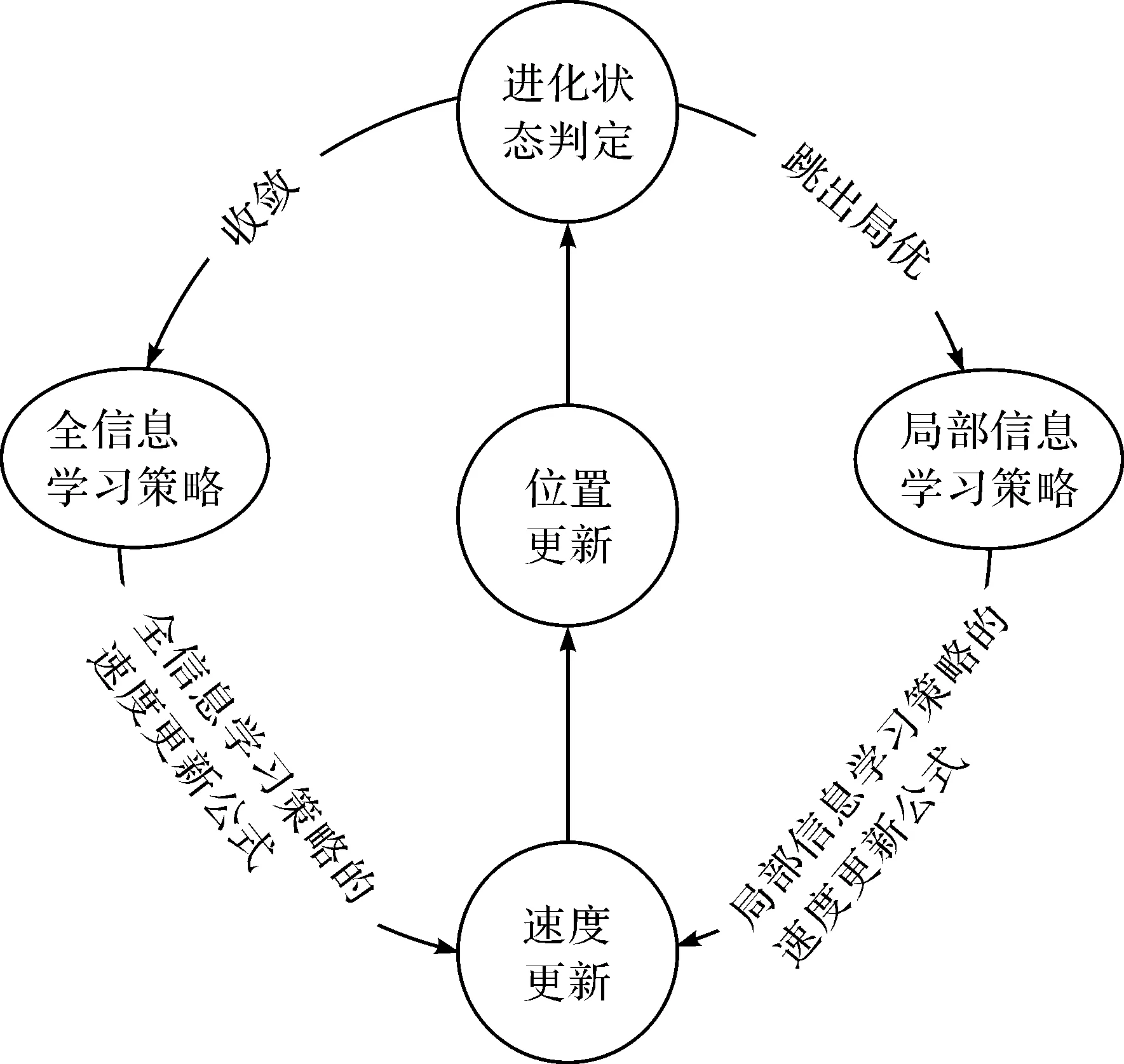
图1 算法优化机制Fig.1 Algorithm optimization mechanism

2 实验仿真及分析

2.1 实验设置

2.1.1 测试函数

为了评估改进算法的性能，笔者选择广泛使用的8 种基准函数进行测试，包括单峰函数F1，F2，F3，复杂的多峰函数F4，F5，F6，最优值不为0 的函数F7和F8。与连续空间中的粒子群优化算法不同，用于离散空间的二进制粒子群算法中粒子的取值只有0和1，具体基准函数及其参数如表1所示。

表1 基准函数及其参数Table1 Benchmark function and its parameters

2.1.2 对比算法参数设置

为了进一步验证所提算法性能，笔者选择以下3 种算法作为对比算法：BPSO，FIBPSO和SIBPSO算法，并从最优值、均值、平均误差、P值4 个方面判断这4 种算法的优劣。BPSO属于基本的二进制粒子群算法；FIBPSO为采用全信息学习策略的二进制粒子群优化算法；SIBPSO为采用局部信息学习策略的二进制粒子群优化算法；笔者所提出的ELBPSO算法依据种群进化状态选择合适的信息学习策略。

拓扑结构的密集程度会影响粒子群算法的性能[15,18]，当邻域粒子数量为5时可以很好地平衡粒子群算法的探索与开发过程。参照对比算法文献，本次实验所有算法的粒子种群规模均为20，最大迭代次数300，领域粒子数量5，维度300，BPSO采用线性递减的惯性权重调整方案。4 种算法的参数设置如表2所示。

表2 算法参数设置Table 2 Algorithm parameters set

2.2 实验结果及分析

表3为BPSO，FIBPSO，SIBPSO和FIBPSO算法求解F1～F88个基准函数所获得的均值和方差，最优值用加粗表示，所需算法的实验数据均为在实验平台上独立运行30 次获得。

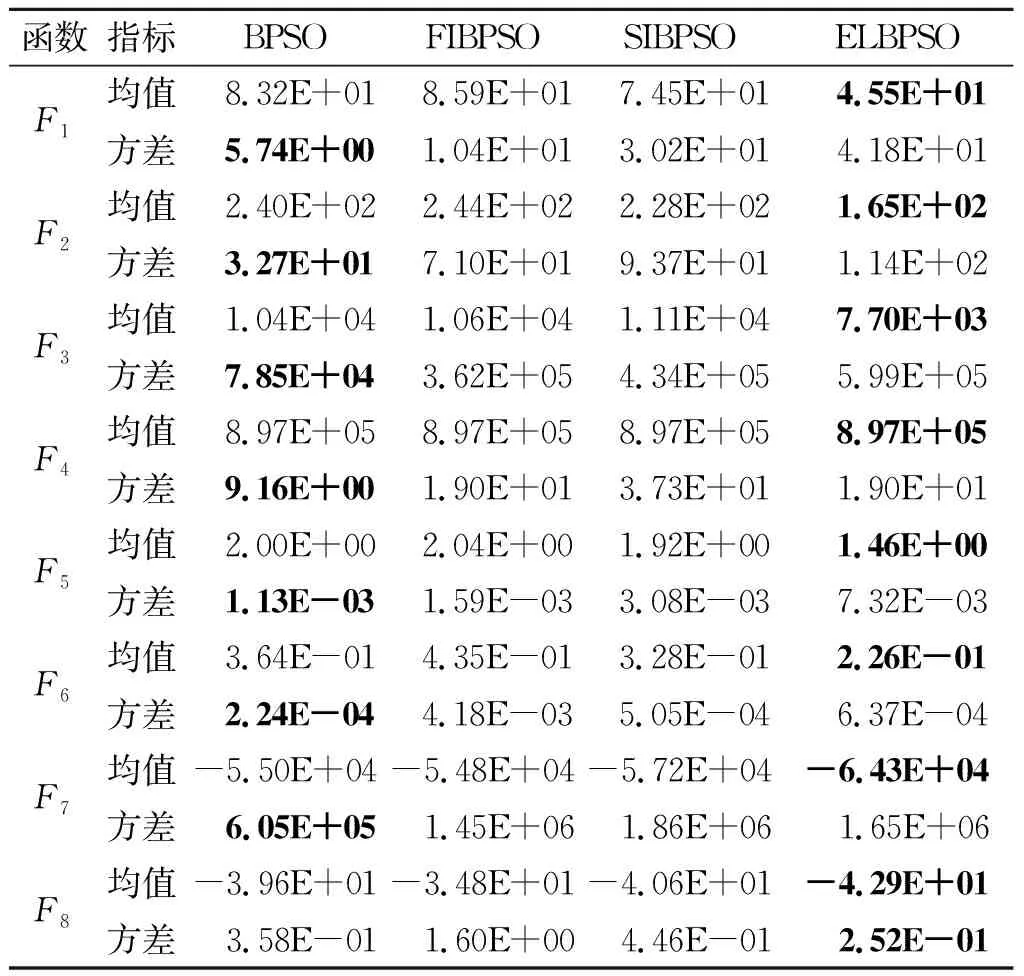
表3 仿真实验结果Table 3 Simulation experimental results

由表3可知：从整体来看，不管在单峰、多峰还是最优值不为0的测试函数中，BPSO算法方差均最小，表现出良好的稳定性，ELBPSO次之，其他算法稳定性较差，这是因为BPSO采用传统学习策略不易受其他粒子影响，求解稳定，而其他算法依据邻域粒子来更新速度和位置，接收的信息较多，导致最优解波动较大。在F1～F88个基准函数上，ELBPSO算法得到的均值最小，对问题的适应能力更强。该算法依据种群进化状态选择合适的信息学习策略，在保证收敛精度的同时不易陷入局部最优，优化了算法性能。

图2为4 种算法在8 种基准函数上、维度为300的情况下所生成的函数值收敛曲线。

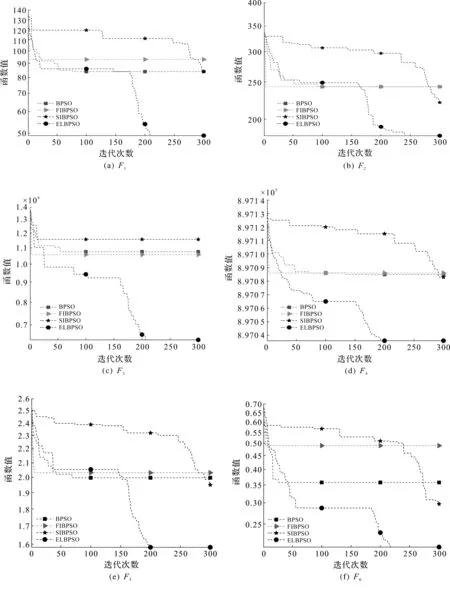
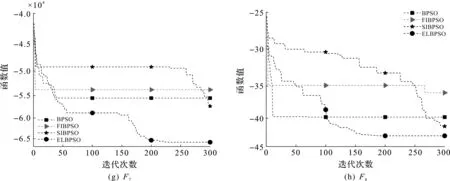
图2 算法收敛曲线Fig.2 Algorithm convergence curve

图2可以更加直观地了解这4 种算法的收敛过程。由图2可知：FIBPSO采用全信息学习策略，受其他粒子的影响较大，前期收敛快但适应度值较大且不再变化，容易陷入局部最优；SIBPSO采用局部信息学习策略，受其他粒子的影响较小，前期收敛速度较慢但后期全局探索能力较强；ELBPSO算法在几乎所有的单峰函数、多峰函数上都显示出了极佳的搜索性能，全局探索和局部开发能力优于对比算法。这是因为在迭代过程中算法依据种群进化状态选择合适的信息学习策略，在保证算法收敛性能的同时维持了种群多样性，增强了算法的全局搜索能力，使其跳出局部最优。对于不为0的测试函数F7，F8，改进算法ELBPSO的寻优优势不够明显，但从总体来看其具有更强的适应性和寻优性。基于进化状态判定的学习策略更新机制可以有效平衡BPSO的全局和局部搜索能力，提高算法的寻优能力和寻优精度。

为对比4 种算法所得结果是否具有统计学意义上的显著性差异，对4 种算法结果进行了威尔科克森符号秩检验，检验结果如表4所示。

表4 威尔科克森符号秩检验结果Table 4 The result of Wilcoxon signed-rank test

由表4可知：除了BPSO与FIBPSO在少部分函数不存在显著性差异外，其他任意算法之间都存在显著差异。对比实验结果均值及P值可以证实笔者所提出的ELBPSO算法性能明显优于其他对比算法，说明基于进化状态判定的学习策略更新机制对二进制粒子群算法性能的提升是有效的。

图3为4 种算法在8 个基准函数上的解集箱图。

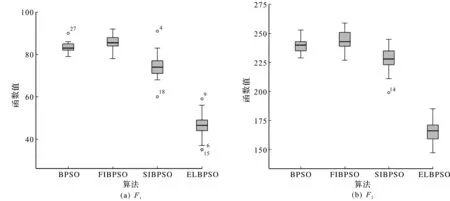
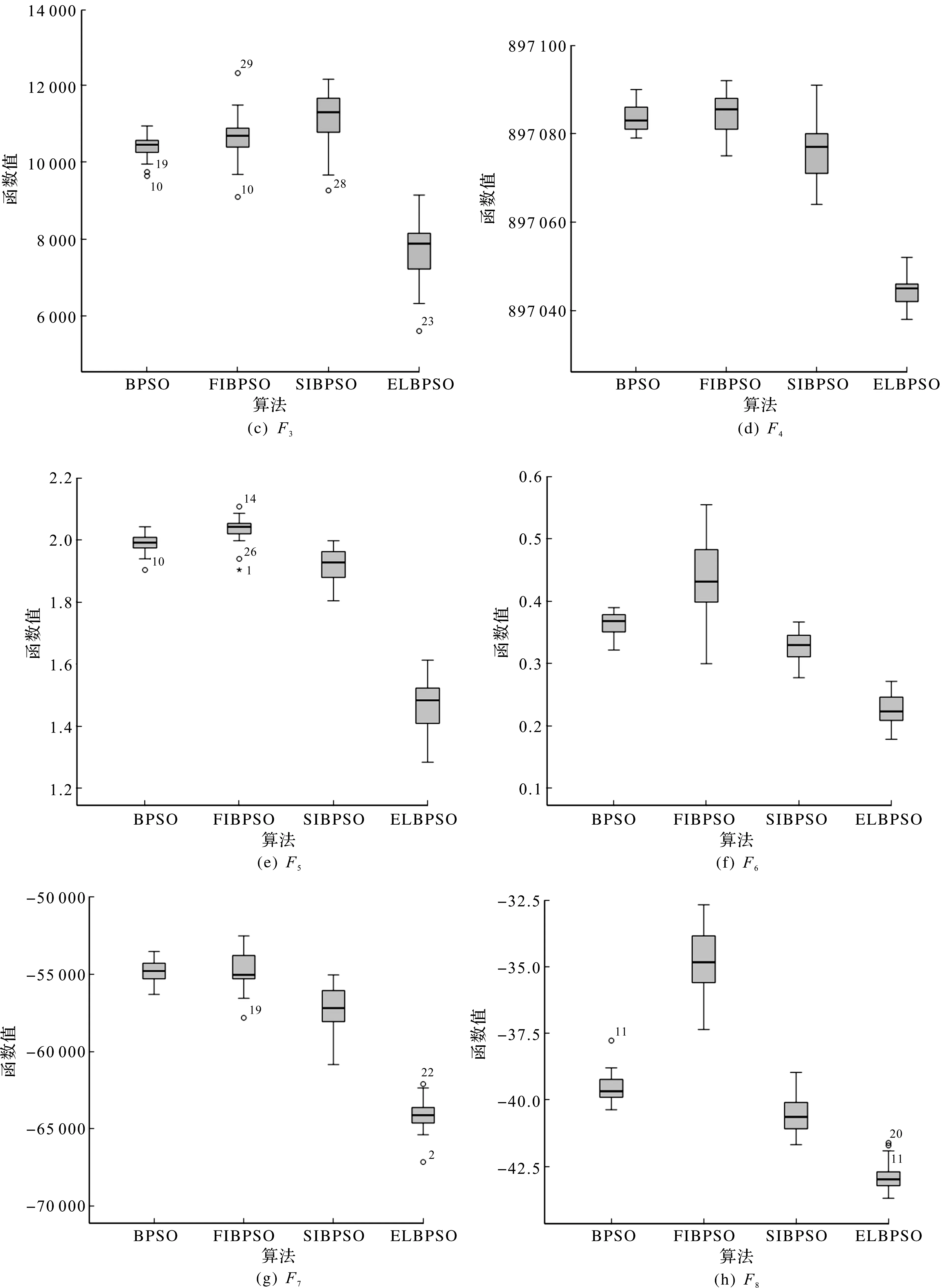
图3 算法最优解统计分布图Fig.3 Algorithm optimal data distribution map

图3可以更加直观地对比4 种算法解集的分布情况。由图3可知：从整体来看，所有算法中ELBPSO更加接近横坐标轴，与图2的检验、收敛曲线一致，验证了该算法的收敛性能远优于其他算法；从解集分布来看，BPSO分布较小而其他算法分布较广，与表3的方差一致；BPSO，FIBPSO以及SIBPSO在最优值不为0的F7，F8函数表现稳定，但在其他函数出现了异常值，且有时不止一个，ELBPSO在最优值不为0的F7，F8函数都出现了一定的异常值，在最优值为0的F1，F3函数虽出现了异常值，但数量不多，说明对大多数测试函数来说ELBPSO的稳定性和收敛性效果较佳，BPSO虽稳定性较好，但解集质量寻优性远不及ELBPSO算法。因此，ELBPSO算法具有收敛快、寻优强、稳定性较好的优点，是一种有效的算法。

2.3 参数敏感性检验

2.3.1 控制系数k检验

为了检验式(3)中调整系数k的敏感性，采用相同实验条件选取函数F1，F5，对笔者所提ELBPSO算法进行30 次实验，观察k变化时算法最优解均值的变化，结果如表5，6所示。

表5 k变化时F1函数最优解均值

表6 k变化时F5函数最优解均值

图4为不同k值下F1，F5函数最优解均值的变化情况。

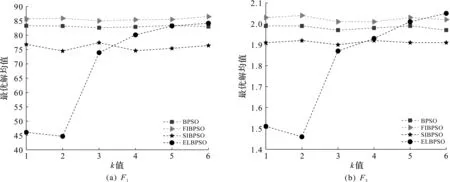
图4 不同k值下算法最优解变化情况Fig.4 Algorithm optimal solution average change for different k values

由图4可知：随着k值的变化ELBPSO算法的收敛精度发生了很大的改变，k的取值在1～2时改进算法最优解均值较为良好，否则寻优性能下降，不具备明显优势，说明ELBPSO算法对k值具有一定的敏感性。实验中取k=2。

2.3.2 进化因子检验

依据进化因子对种群进化状态进行判定是信息学习策略更新的关键。ELBPSO中进化因子判定值越小，采用全信息学习策略的机会就越大，利于算法收敛，但易陷入局部最优；判定值越大算法选择局部信息学习策略的机会就越大，利于维持种群多样性，使算法跳出局部最优，但收敛性能不佳。为了检验进化因子判定的最佳状态和敏感性，在相同实验条件下调整E的判定值，对所提ELBPSO算法进行30 次试验，观察E值变化。计算F1，F5函数最优解均值，结果如表7，8所示。

表7 E变化时F1函数最优解均值

表8 E变化时F5函数最优解均值

由表7，8可知：当进化因子E=0.7时ELBPSO在F1，F5函数最优解均值最小，算法性能最好。

图5为不同E值下F1，F5函数最优解均值的变化情况。

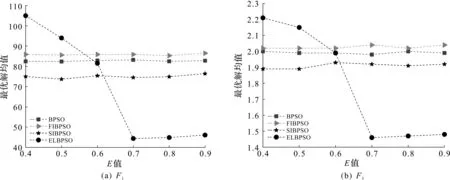
图5 不同E值下算法最优解变化情况Fig.5 Algorithm optimal solution average change for different E values

由图5可知：ELBPSO的最优解均值随着E的变化而发生波动，说明进化因子判定值的变化对函数求解影响较大。E为0.7时可以很好地平衡收敛并跳出局部最优，因此实验取E=0.7。

3 算例分析

为检验优化方法的实践性能，笔者从网络上挑选部分学习资源，利用以上算法给学习者进行推荐。学习资源包含媒介类型、难度水平、内容类型属性，学习者包含学习风格、能力水平、认知水平属性，学习资源推荐本质是对学习资源属性、学习者属性进行匹配，求出差异最小解，确保推荐资源的属性与学习者特征属性相匹配。为提高算法求解效率，构建目标函数将资源推荐问题抽象为数学问题，问题求解的适应度值越低表明学习资源越符合学习者特征，利于个性化学习。实验设置124 个学习资源，各算法寻优得出的推荐资源序列结果如图6所示，1表示向学习者推荐对应序号的学习资源，0表示不推荐。

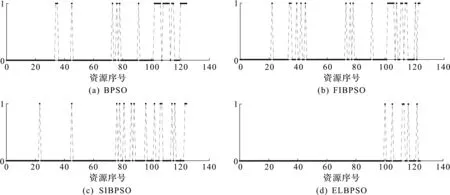
图6 不同算法下学习资源推荐结果Fig.6 Learning resource recommendation result under different algorithm

由图6可知：改进算法能准确求解优化问题，表明了算法执行逻辑的正确性；不同算法推荐资源的序号、数量各不相同，推荐结果存在较大差异。

图7为各算法求解资源推荐问题的适应度值。

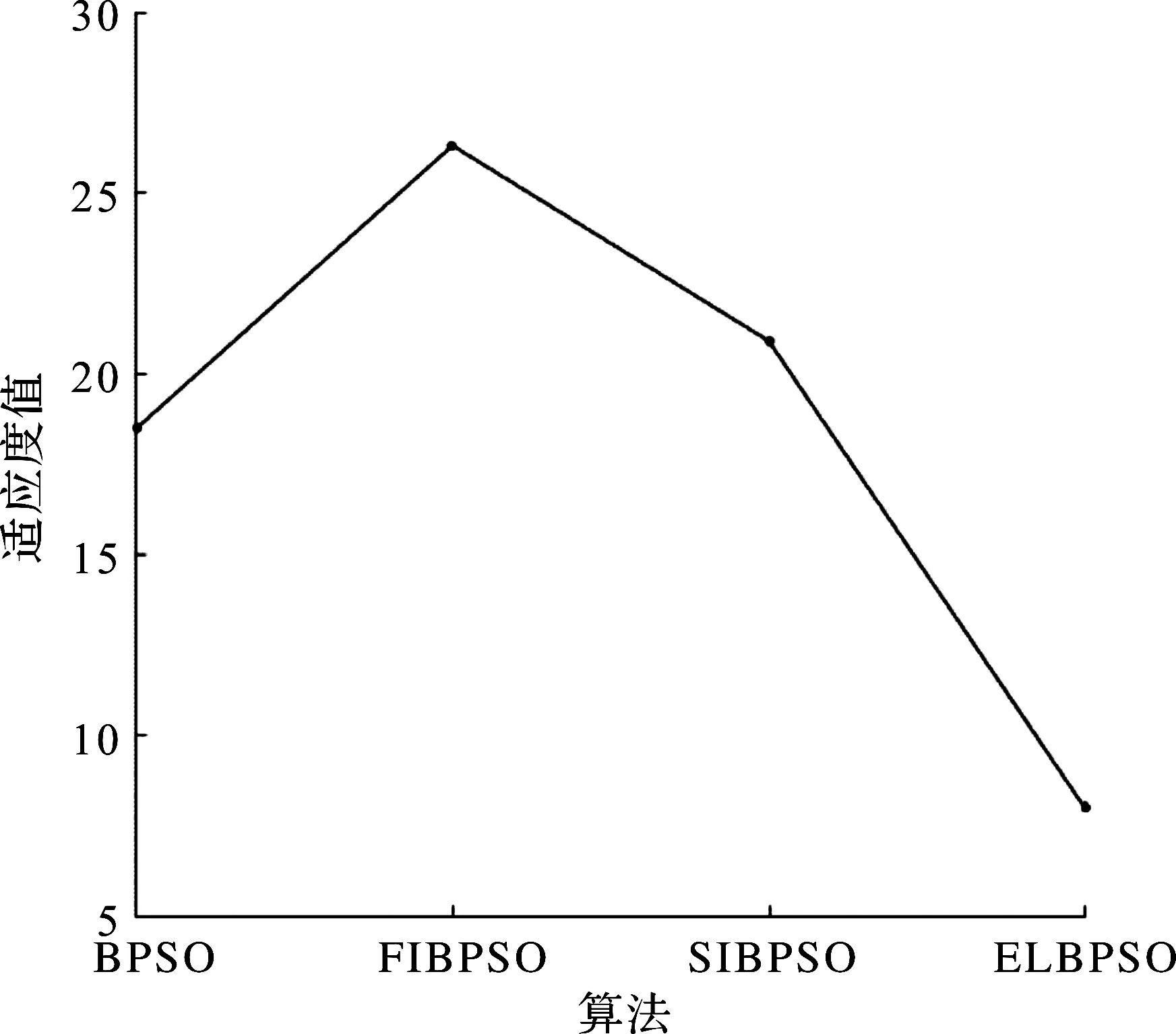
图7 学习资源推荐适应度值Fig.7 Learning resource recommendation fitness value

由图7可知：ELBPSO算法求解的适应度值最低，SIBPSO算法和BPSO算法次之，FIBPSO算法的求解结果最大，表明笔者改进的算法不仅能对优化问题成功寻优，同时也具备良好的寻优性能。

4 结 论

笔者依据种群进化状态采用学习策略更新机制对二进制粒子群算法进行优化，有效平衡了收敛与跳出局部最优的状态，在保证算法具有较强开发能力的同时，提高了算法后期全局探索的能力，避免陷入局部最优。实验结果表明：ELBPSO算法对单峰函数和多峰函数具有更高收敛速度和精度，但对复杂的最优值不为0的函数改进优势不够明显，仍有很大的改进空间，今后将对这类问题的优化进行更加深入的研究。