“放大”只为了“深刻”这份情谊

鲍莉丽

[摘要]数学教学重在教人思考。针对怎样的“教”能够促进学生深入地“学”，如何激发学生的思考力来促进数学本质的探索等问题展开思考，力求运用“放大”的艺术来促进数学课堂的美好展示。课前，站在学生已有经验的基础上放大未知领域，放大知识内涵，及时对知识进行整合和再创造;课中，也要适时适地放大学生的疑惑和错误，使疑惑得以解决，错误得以升华，使“教”真正地为学生的“学”服务！

[关键词]教学艺术;放大;数学课堂

[中图分类号]

G623.5

[文献标识码]A

[文章编号] 1007-9068（ 2020）29-0008-03

许多专家学者一直呼吁：数学教学应站在儿童立场之上，要让儿童用自己的方式去接近数学。佐藤学说：“教育往往要在缓慢的过程中才能沉淀一些有用的东西。”然而，作为一名数学教师，一直立足于教学一线，如何在自己的数学课堂中展现这样的理念，为学生的未来而开展负责任的“教”呢？郑毓信教授说：“数学教育的一个主要目的就是通过数学帮助学生学会思维，并能逐步学会想得更清晰、更全面、更深刻、更合理。”如何培养学生的思考力？如何促进学生进行深刻的学习？如何让数学的学习有价值？那就是善用“放大”的艺术，让数学教学往“深刻”中走！

一、放大未知再创造

对于现阶段的数学知识，学生已然不是零起点，同时对于某些技能和方法，学生或许也已掌握得炉火纯青。然而，学生真正理解这些知识背后的数学本质和数学思想吗？在教学之前，教师得充分了解学生的“已知”，在此基础上适时地放大未知，进而再创造。

“三角形的内角和”这一内容，就是这样的一节“课前学生已經知道了相关内容和结论”的课。如果按照教材的编排，忽略学生的已有经验，从零起点着手，那课堂上会出现学生无学习动机、无探究欲望的真实情境。这样的课还有必要上吗？特级教师顾志能对这节课的思考和剖析给了我很大的启发和触动。课前，顾老师对学生的已有认知非常了解——学生知道的只是“三角形的内角和是180°”这一结论，他们既没有深刻地经历这一知识形成的过程，也没有通过这一知识的学习积累数学的活动经验，感悟数学的思想方法。因此，顾老师就从问题“真的吗？”人手，要求学生进行多方法、多角度的验证;然后，抛出问题：“为什么不管什么形状、大小的三角形，内角和总是180°？”再次引发学生的探究欲望，通过探索和实践，最终得出了“无论怎样变形.三角形的三个角都在相互制约，从而导致了内角和不变”的完美解释。可以说，通过这样的探究活动，学生的空间观念得到了质的发展。最后，顾老师又针对三角形内角和的价值性进行了提问，成功地激起了学生强烈的探究欲望。

“真的吗？为什么？有什么用？”这三个问题串出了一节课。顾老师对“三角形的内角和”这节课的各个环节的处理让我更加明白了，在数学教学中，让学生仅仅记住一个结论或者一种方法技能，显然是远远不够的。这不由得让我想到了“认识长方体”这节课，像“什么是长方体？”“长方形有几个面？”等问题在学生的心中早已不是困惑，对此他们早就有了丰富的经验，教师就需要在此基础上放大未知，本着“发展空间观念”这一上位目标对教学进行改造和设计。比如，在和学生初步总结了“长方体的六个面都是长方形，相对的面完全相同”的基本特征后，出示一个长方形（一张纸）——长3分米、宽2分米，提问：“要围成一个长方体，还缺几个面？你能想象出另外的五个面分别是怎样的长方形吗？”凭借想象，学生对“长方体的六个面”自然就能真正建立表象，这六个面也才能真正植入他们的脑海里。通过这样的反复拆分（拼接）的过程，学生不仅更加深刻地理解了面与面之间的联系，还理解了棱与面之间的关系。之后探索与研究“棱”时，学生画长方体的透视图便水到渠成了。此时，“只需知一条长、一条宽、一条高能够决定一个长方体”的经验就赫然在前。多么完美的诠释啊！

因为有循序渐进的过程，所以对于长方体中的“未知”部分学生能够很好地与头脑中的“已知”进行衔接，从而在未知领域中深化认识，接近数学的本质。在平时的教学中，教师如果能时刻站在学生“已知”的基础上，多展开一些“未知”方面的追问，就一定能帮助学生明白知识背后的价值是什么，也一定能促进学生进行更为深刻的思考。

二、放大疑惑思且行

从某种意义上来讲，教学就是为了解疑释惑而存在的。实践证明，学生的学习经验，不仅要暴露，而且要尽早暴露。因为暴露得越早，就能够尽早地发现学生的疑惑，进而有效应对和巧妙利用。

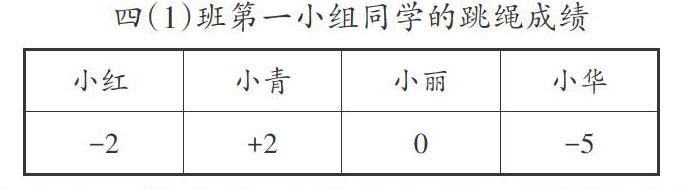
在一次有关“深度学习”的展示课上，某教师执教的内容是“认识正负数”，在引导学生借助数轴理解正负数是两个相反的量，深刻理解了“0”表示的意义之后，教师出示了一个表格，请学生思考并回答第一小组的同学分别跳了多少下。

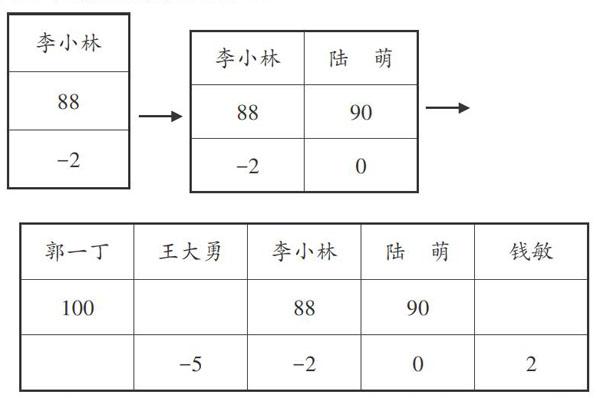
在交流反馈阶段，有位女生质疑：“跳绳要么没有跳，要么跳了，怎么可能会‘-2呢？”这样的发问让教师始料不及，显然这超出了教学的预设。这引起了我的思索：这位女生为什么会有这样的疑惑呢？是对正负数意义的理解还不够深入透彻吗？课后，我反复地翻看笔记，突然想起了特级教师周卫东在执教这节课时的情景。当时，周老师也用了相同的素材，只不过他是这样引导学生思考的：李小林期末考试考了88分，可是他看到老师在估计平均分时，却用了这样的表示方法（如下图），猜一猜这是什么意思呢？周老师首先出示的是李小林的成绩，再出示陆萌的成绩，之后，再逐一出示其他三个同学的成绩，以此引导学生明白正负数的相对意义。

两者一比较，就能知道同样的素材为什么会有不一样的效果。在前面那位教师的课上，这些数据的一并出现，其实是会给学生非常突兀的感觉，学生一时间无法接受，也理解不了这样的表述方式。从具体的数据到正负数相对性的表示的过渡，学生的思维是需要一个“跳板”的。有了参照对比，我瞬间就明白了课上那位女生的疑惑其实是她内心最为真实的想法。

“放大疑惑看课堂”，学生思维的衍生可以更为自然、更为深入。“放大学生疑惑”实际上能帮助教师去探寻课堂的切人点，去理解学生的真正需求和真实的情感体验，思考当下的教学应该怎样更好、更妙地前进。

三、放大错误促理解

“人生就像一场旅行，不必在乎目的地，在乎的是沿途的风景，以及看风景的心情。”数学教学如同旅行，应该在乎的是学生的学习过程，应该关注学生在学习中产生的错误，因为透过一个错误，教师可以知晓学生的思维方式和产生错误的根源。

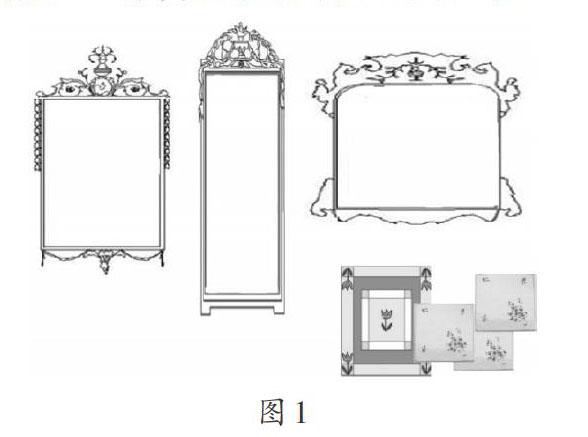
在一次的学区赛课上，我教学的内容是北师大版教材三年级下册的“什么是面積”。课上，在引导学生比较物体表面的面积大小时，有一个环节我是这样设计的（如图1），抛出的问题是：请比较三个镜面的面积大小。而在三面镜子的下方，我提供了两款大小不一样的手帕，希望学生在摆手帕的过程中产生认知冲突——手帕不一样，镜面的面积无法比较。

然而，当课件展示（如图2）结论时，学生竟毫无异议地得出“第一面镜子和第二面镜子一样大，第三面镜子最大”的结论。听到这样的回答，我心里顿时一惊：预期的情况没有出现，怎么办？是直接点出“手帕大小不同”这一关键元素吗？不行！这绝对不是一个好的路径。我的大脑开始飞速地转动着：学生为什么会有这样错误的判断？他们的基准点在哪？我决定抓住这宝贵的错误资源，挖掘其中隐含的数学本质。

于是，我提问：“你们是怎么得出这样的结论的？”有学生解释：“因为第三面镜子上的手帕刚好是小手帕的2倍，这样的话，大的两块刚好就是小的4块。”我追问：“你是怎么确定第三面镜子上的手帕是小手帕的2倍的？”“我猜的。”“哦，我明白了，你的意思是手帕大小不一样，不好比较，要换成一样大的手帕才可以比较，是吗？”

就在这样的一问一答中，我给这个意外的错误拨正了“身份”，也让学生明白了比较大小需要一个相同的东西做参照。可见，当时的多一秒思考使这个错误成为课堂上的最强生长点。

建构主义理论指出，学习不是由教师把知识简单地传递给学生，而是要由学生自己建构所得。“放大错误”，学生便会面临挑战和阻拦，就会主动地调动已有的经验，充分激发自我的潜能进行深入思考，这时候，主动探究便成为学生的一种迫切需求。这些难道不是教育的初衷吗？

四、放大内涵润本质

《教学勇气》的作者帕克·帕尔默认为，教室中还有第三者存在，并不只是教师和学生，还应该有我们所学的学科。挖掘教材内涵开展设计，课才能变得厚实。因此，教学重点要努力凸显，多花一些时间，多用一些策略，反复刺激，不断强化;教学难点要敢于直面，要多一些创新的勇气和智慧，抓住要害，巧妙应对。

比如，对于“角的初步认识”，要思考的是怎样让学生对“角”有深刻的认识。于是，有位教师就从精选素材上人手，先用小圆片、点子图和吸管进行有指向性的操作活动——创造直角，使学生明确直角是一类特殊的角;接着再次精剪素材，只用吸管继续制作锐角和钝角。这样的活动，其实就是放大了角的相关知识内容，使学生真正有时间、有机会去理解概念的内涵，从中也感知到了角的大小和张口有关，了解到了锐角、直角和钝角之间的大小关系，聚焦了知识本质。

又如，教学“三角形的三边关系”时，一般的做法就是给学生三根小棒，让学生通过围一围得出“三角形两边之和一定大于第三边”的结论。然而，这样理想化的结论在现实操作中是无法达到的，因为不可能确保三根小棒的长度剪得很精确，不差0.1毫米或0.01毫米。因此，通过动手操作得到的结论是：哪怕是两条短边之和等于长边时，也是可以围成三角形的。如何让学生信服“围不成”这个结论呢？不妨放大“三角形三边”的内涵，即数学上的三条线段，是抽象的产物，说是几厘米就是几厘米，是毫无误差的，因为数学上的线段是没有宽度的。这样是不是就能脱离现实中的小棒了？

特级教师顾志能就充分放大了“两个短边之和等于长边，能否围成三角形”这个点，利用课件演示三边的运动，学生通过想象，从三边的运动轨迹中深刻地理解了“两个短边之和等于长边，不能围成三角形”的数学原理。这样的设计实在是既巧妙又完美！在我看来，顾老师这样处理，不仅仅是为了突破难点，更是为了发展学生的思维能力。

而如何突出重点，突破难点，才是对教师教学智慧与能力的真正挑战。于是，我开始尝试用放大内涵的策略，在教学前追问“是什么”“为什么”“怎么做”“为何这样做”“一定这样吗？”这五个问题，以此使数学本质得以凸显。

特级教师周卫东说：“所谓教育，不过是一场顺势而为。顺应儿童成长之理，处儿童成长之势，给予生命的关怀。”纪伯伦说：“不要因为走得太远，忘了为什么出发。”我们不要忘记了教育的初心：为了学生能够更加深刻地学习数学，为了带走有用的东西。相信善用“放大”的艺术，一定能帮助我们的教学攀上最接近数学本质的那座高峰。

（责编金铃）