如何让数学课更有“数学味”

周卫东

[摘要]长期的课堂教学实践使我们认识到，倘若在课堂教学中注重数学内容的揭示、教给学生数学知识的同时，还能揭示知识的发生发展过程，揭示解题方法和规律的抽象概括过程，让学生较为深入地领悟数学的内涵（即“数学味”），一定能促进学生数学素养的全面提升。在教学内容中找寻“数学味”的配方，在教学过程中探寻“数学味”的实质，在数学思想中触碰“数学味”的灵魂，在数学文化中品尝“数学味”的芳香，才能让数学课更有“数学味”。

[关键词]数学味;教学内容;教学过程;数学思想;数学文化

[中图分类号]

G623.5

[文献标识码]A

[文章编号] 1007-9068（ 2020） 29-0001-03

追求“数学昧”永远是数学教学的第一要务。要让数学课有“数学味”，不是一种简单的技巧，它不像“泡汤”一样，只要把“数学”放到汤碗里搅拌一下，就会出现有“数学”味道的汤，而应该对数学学科的内涵进行系统思考，并进行“智慧加工”，使之逐渐弥漫出“数学”的芳香，从而润泽学生的数学素养。

一、在教学内容中找寻“数学味”的配方

从教材的编排体系来看，数学教材由两条“河流”组成：由具体知识构成的、易于被发现的“明河流”和由数学内涵构成的、具有潜在价值的“暗河流”。这两条“河流”是骨架与血脉的关系。有了数学内涵做灵魂，各种具体的数学知识才不成为孤立的、零散的东西。正因为有了数学内涵，“游离”状态的知识才会凝结成优化的知识结构，形成一个有机的整体。只有做到“看书要看到底，书要看透，要看到书背面的东西”（苏步青），充分挖掘数学教材中的灵魂——数学内涵，用数学内涵引领课堂教学，才能高屋建瓴，提契整个知识体系，进行再创造、再建构。

比如，人教版教材一年级上册中的“1-5的认识”，以一个温馨兴旺的农家生活“大场景”，引导学生正确建立“1-5”各数的概念。教材蕴含着从不同的角度对数进行抽象的数学思想：关于1，有1位老奶奶、1个面盆和1只可爱的小狗;关于2，有2只鹅、2个竹筐、2个鸡食盘;关于3，有3只鸟、3盆花……画面的多姿多彩，不仅仅是为了美观，还充分说明：同一个数，可以表示植物的多少也可以表示动物的多少，可以表示有生命事物的多少，也可以表示无生命事物的多少，可以是灰色的，也可以是彩色的，表明元素的多少与物体的属性没有关系;在确定一个集合的元素有多少时，不需要用完整的物体来表示，可以用物体的一个部分来表示，但这一部分必须和物体存在一一对应的关系;在确定一个集合的元素有多少时，表示的不仅仅可以是地上的物体，也可以是天上飞的，这说明对数的抽象无处不在，世界上到处充满数。只有意识到这些数的“内涵”，数学教学才能走得更远，才能更具生长力。

从教学层次的角度来分析，数学课堂教学设计应分宏观设计、微观设计和情境设计，教学设计应充分从这三个层面进行分析、思考。无论哪个层次上的设计，其目的都是让学生参与到获得和发展认知的数学活动中。因此，教学设计不能只停留在数学认识过程中的“还原”，更应该有数学内涵的飞跃和创造。

以空间与图形领域中“图形与位置”内容的安排为例。这部分内容主要包括二年级用“第几排第几个”的方式描述物体的位置，五年级用“数对”表示方格图上点的位置，以及六年级用“方向和距离”表示平面图上点的位置。上述内容中所蕴含的数学内涵主线是“依据小学生的年龄特点和认知水平，让他们逐步感知数与平面图形上点的关系，培养符号感，体会数形结合的基本方法和价值”。其中，用“第几排第几个”的方式描述物体的位置，主要着眼于学生已有的生活经验;用“有序数对”表示方格图上点的位置，则是对生活经验的提炼，也是对感性认识的提升;用”方向和距离”确定平面图上点的位置，其基本思想与用“数对”表示点的位置是类似的，但它引导学生从不同角度认识相关数学知识的内涵。因此，这就需要搞清楚不同内容应怎样概括共性，相似内容应该怎样区别个性，而要顺利地完成这一任务，必须依靠数学内涵作为核心指导，有了深刻的数学内涵做指导，才能设计出智慧灵动的教学思路，才能引发学生创造性的思维活动。

二、在教学过程中探寻“数学味”的实质

数学内涵往往呈隐蔽形式，沉积、凝聚在数学结论的背后，常常渗透在学生获得知识和解决问题的过程中。著名数学家波利亚认为：“学习任何知识的最佳途径，都是由自己去发现、探究，因为這种理解最深刻，也最容易掌握其中的内在规律、性质和联系。”教师应该有效地引导学生经历知识形成的过程，让学生在观察、实验、分析、抽象、概括的过程中，积累数学活动经验，提升数学思考的能力。只有如此，学生所掌握的知识才是鲜活的，这样的学习才是充满智慧的。

在人教版教材五年级上册“用数对确定位置”一课的教学中，我努力使学生获得有价值的思维空间，体验到数学的价值和魅力。

在学生掌握了用数对描述位置的基本方法后，我创设以下问题，以引发学生的数学思考。

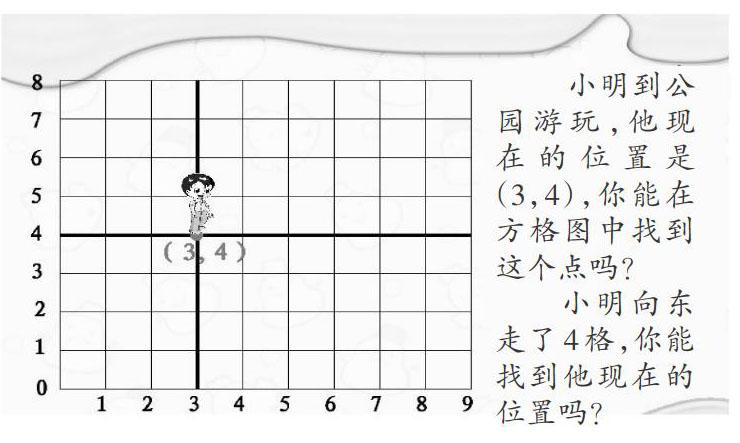
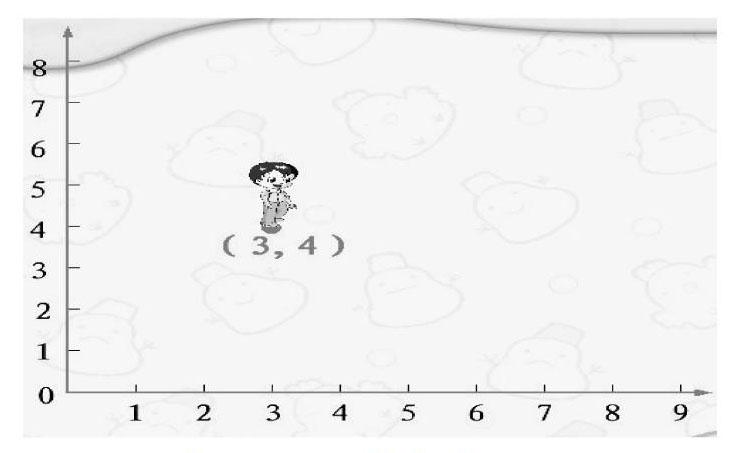
师：小明在运动之前的位置是（3，4），现在的位置是（7，4），你能看出这两个数对之间的联系吗？

生1：这两个数对的后一个数都是4。

生2：后一个数之所以没有变化，是因为他运动的前后都在同一行，所以后一个数都是4。

生3：我看出了前一个数由3变成了7，是因为他向东走了4格。

生4：用3加上4就是7了。

师：不简单！假如小明向东走了20格，他的位置是多少？如果向东走了50格，位置又是多少呢？

师：小明改变了运动方式，他运动后的位置是（3，20），你知道他是怎么走的吗？

生5：我认为小明是向北走的。

生6：我同意生5的意见，而且小明走了16格。

师：看得出，同学们对方格图上点的位置变化已经掌握得比较清晰了。不妨再深入思考，以点（3，4）为例，你是怎么找到这个点的？

师：你认为哪几根线可以决定这个点的位置？（学生分别指出表示第3列的直线和表示第4行的直线）

师：咱们的思考不妨再深入一点。这两根线又是由哪些线决定的呢？（学生感受到问题很有意思，非常兴奋;有学生指出最左边和最下面的两条线）

师：其实，有了这两条线，也就能决定图中任何一点的位置。没想到，我这一带，竟带出了一群中学生，这一知识将在中学的学习中有进一步的研究。

在此教学片段中，教师采取数形结合的方式，抓住运动前后数对的变化，引导学生分析、对比、想象、概括，得出了数对的变化规律，有效地训练了学生观察、对比、抽象、概括等多元的数学能力。让学生在方格图中找点，体会到找点的方法，再通过“是怎样的线条决定了方格图中点的位置”，感悟纵横交错两条线的作用，进而得出横轴和纵轴在确定位置中的作用，凸显了确定数对时的关键点。课上教师的一句“这一带，竟带出了一群中学生”，润物无声的知识结构渗透，让学生在感受符号体系的过程中感受到相应的数学价值，帮助学生建立起大数学的宏观视野。

三、在数学思想中触碰“数学味”的灵魂

“在一切方法的背后，如果没有一种生机勃勃的精神，它们到头来，不过是笨拙的工具。”这里的精神指的就是数学思想。从哲学角度来看，“思想”即“观念”，即社会存在于意识中的反映。而所谓数学思想，是人们对数学研究统一的本质性认识，是指现实世界的空间形式和数量关系反映到人的意识之中，经过思维活动而产生的结果，是被人们反复运用和确认，且带有普遍意义和相对稳定的特征的，它直接支配着数学的实践活动.是对数学规律的理性认识。由此看来，数学思想是数学内涵的核心，它决定了数学的经验基础、思考核心和发展目标。

从宏观角度看，小学数学思想按研究层次不同大致可分为以下几类：一为哲学的（包括逻辑的）思想，如分析法、综合法、演绎法、归纳法、类比法等;二为科学的思想，如实验法、图表法、假设法等;三为数学的思想，如化归法、递推法、列举筛选法等。前者应当是整个数学教学的主线，是最上位的思想，但在具体的问题中，会涉及数学抽象、数学模型、等量替换、数形结合等数学思想。数学思想的形成同样有一个循序渐进的过程，只有经过理解、应用、促疑，才能使学生真正领会，并形成自觉运用数学思想的意识，建立起自我的“数学思想系统”。

比如，教学“三角形的三边关系”，在学生已经初步掌握了“两边之和大于第三边”这一规律后，北京名师孙贵合老师设计了这样一个问题来驱动学生的思维向思想层面“跃升”：有两根小棒，一根长7厘米，另一根长9厘米，把其中一根小棒剪成两段，用拼的方法，你能将它围成一个三角形吗？学生带着这样的“任务”走了自己的“世界”里，思维成果不断涌现。

生1：不可以把短的小棒剪成两根，因为“两边之和大于第三边”是指较短的两边之和应该大于第三边，只能把长的剪成两段。

生2：我把长9厘米的小棒分成了4和5，3和6，2和7，1和8。

生3：他说错了，不可以分成1和8。如果这样分，两条短边是1和7，长边是8，这样两边之和就等于第三边了。

师：了不起！不仅找出了答案，还洞察到其中的细微之处。相信同学们对今天所学的规律理解得更为透彻了！

师：让我们把这几种情况画下来。

师：除了这几种情况外，还有其他可能吗？

生4（迟疑地）：剪开的两条边的长度可以是小数吗？

师：明白他的意思吗？能不能举一些例子？

生5：比如，9可以分成4.1和4.9，3.1和5.9。

生6：9可以分成2.1和6.9，9可以分成1.1和7.9。

生7：9可以分成2.12和6.88，9可以分成1.16和7.84。

师：这些都可以拼成三角形吗？

生（齐）：能！

生8：这些都能满足“两边之和大于第三边”的条件。

师：太好了！一共有多少种可能呢？

生（齐）：无数种。

师：让我们把些可能性也用图表示出来。想象一下，如果把这些点都描出来，这幅图像什么？

生9：像鸟巢。

生10：像国家大剧院。

“‘无限这一主题不应被看成与小学数学完全无关的，如何能够通过有关的内容帮助学生建立起关于无限的一些认识，就是小学数学的重要目标。”（郑毓信语）在上述教学中，三角形三边之间的关系在多种可能性中不断地被强化、被“结构”，由边的长度（整数、一位小数、两位小数，甚至更多位小数）可能性的拓展，在学生脑中逐渐形成一个“无数”点的集合，这不就是“极限思想”的有机渗透吗？

不仅如此，两条不断变化着的短边的长度与固定的长边之间，形成一个a+b>c（其中a

四、在数学文化中品尝“数学味”的芳香

华东师范大学教授张奠宙在一篇文章中写道：“我希望我们大家来了解数学，有三个层面：一个层面就是公式定理，像勾股定理、求根公式等;第二个层面就是思想，就是我们的公理化思想、数形结合、函数思想等;还有一个层次就是文化价值。”的确，数学是人类实践活动的产物，社会与文化不仅推动着数学的发展，同时数学也是推动社会与文化发展的关键性因素。

从表面来看，任何教学所传播的总是文化，而且是在形态上可以呈现多种多样的文化。传播文化并不意味着教学就是有“文化”内涵的，因为我们所追求的文化，不是那种可见的、物态化的符号，图像或行为，而是一种语言，一种只对它孜孜叩问的人才会彰显的无声语言。

对“善”的向往。数学，如果给它打扮，它就像一位光彩照人的科学女王。但是如果在数学课堂上呈现的仅仅是逻辑，仅仅是枯燥的几个公式，那么数学这个“美女”就变成X光下的骷髅，就是X光的照片。不容否认，数学有着强大的教化功能，有着较浓的“善”的品质，比如探索过程中的执着与坚韧，论证过程中的务实与严谨，创造过程中的开拓与超越，乃至耐心、责任感、敬业品质、民主精神等。数学课堂就要有意地引导学生对“善”产生一种“心向往之”的需要。

对“根”的叩问。意义感的恢复是儿童建构完整人格的前提。意义产生于人与世界相遇的时刻。当我们意识到自己与世界成为一个整体时，我们的生活才具有完满意义，也就是说，世界是意义生成的背景，意义的产生需要使每一个人与这一背景重新建立联系。在课程领域，儿童意义感的恢复需要使之重新与某种超越的东西相连，使课程成为人的内在精神之旅。教师对司空见惯的数学内容总是做成人化的解读，做简单化的诠释，做线性化的推进，很少考虑这一教学内容从哪里来，亦即缺少对“根”叩问的一种姿态。比如，量角器上的刻度为什么要平均分成180份？为什么要有内圈刻度和外圈刻度？量角的时候为什么要做到“点点重合”“边线重合”……这些涉及数学知识的本源问题和元认知等关注“根”的策略，教师理应关注并尽力彰显其丰富的知识内涵。

对“史”的关注。人类发展已有着几千年的历史，沧海桑田的演变，给后代积淀下厚实的数学文化，翻开历史的长卷，古今中外的文化史实犹如一颗颗亮灿灿的明珠镶嵌在历史的长廊上，令人目不暇接。这些宝贵的财富，理应成为我们的教学资源，“雕刻”在学生记忆的深处，成为他们数学素养中不可或缺的一部分。比如，教学“圆周长的计算”时，我运用现代化教育手段呈现刘徽割圆术以及祖冲之的伟大成就，引领学生了解圆周率的探索历程，豐富数学活动内容的同时拓展了学生探索的空间。学生通过观察、联想，发现圆内接正多边形的边数越多，正多边形的周长越接近圆的周长，正多边形的周长与直径的比值越接近圆的周长与直径的比值，从而感受极限思想——圆内接正12 288边形、正24 576边形的边长非常小，从而受到了震撼。了解圆周率的探索历程的活动，是一个领悟数学思想方法的过程，是一个体验科学精神的过程，是一个感受、欣赏数学文化的过程。

（责编金铃）