借助互联网教学，让数学建模课乘风飞翔

孙晓红

[摘  要] 数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养.如何让数学建模课在数学课堂落地生根，是我们一线教师亟待解决的问题. 利用互联网+教学，可在常规课程、选修课程、竞赛课程三个层次由浅入深进行数学建模教学.文章以《生活中的三角函数》的教学设计为例，对数学建模进行深入探讨.

[关键词] 互联网+教学;数学建模;三角函数

？摇为促进创新人才素质培养，青岛二中2014年9月开始实施互联网+教学改革，开展基于学习任务单的课前自主学习，培养学生自主学习能力;开展基于学习社区的学习，培养学生合作学习能力.在学习过程中，按照学生兴趣、特点，建立高效、互补的学习社区，开展课上、课下的合作学习，逐步形成了“生学为本、合作内化、师教为要、点拨升华”的互联网+教学原则. 这样的教学方式使学生从传统教学中知识的被动接受者，转变为知识的主动学习积极获取者，转变为基于学习社区的小组合作学习者，转变为课堂上基于重点问题展开的教学活动的参与研讨者，充分体现了学习者的主体地位. 借助互联网和PAD教学模式，大大提升了学生的学习兴趣，提高了教学效率.以下是高中数学人教B版必修四第一章《三角函数》最后一节“三角函数模型的简单应用”，以往教学都是以例题的形式，展现三角函数的简单应用，突出三角函数作为描述现实世界中周期变化现象的一种数学模型，其在刻画周期变化规律、顶测其未来等方面都发挥着十分重要的作用. 同时，也體现化归转化、方程与函数、数形结合等思想方法在研究解决问题中的作用. 教师在教学中也经常是以例题的形式，层层引入，让学生发现三角函数模型来源于生活、为生活解决实际问题的工具性作用.但这种教学方式对于学生还是被动接受，主动探究的意识不强，对培养数学建模的思想不够完善. 笔者的教学设计是变被动为主动，让学生提前一周查阅资料，查找相关的资源，以小组自主探究、合作学习的模式发现生活中的三角函数，通过生活中周期性变化的事例大胆猜想其与三角函数的关系、建立三角函数模型、把求三角函数解析式的题型放在生活实例中、预测未来的发展趋势，并同时教给学生数学建模的方法. 教学中，笔者让学生做课堂的主人，提升学生的学科核心素养. 以下是本节课的具体教学设计环节.

环节一：课前教学设计

（一）提前一周的学生活动

按照五个教学班把学生分成五组，以“生活中的三角函数”为课题查找材料，选出组长、确定主讲人，学生借助互联网查找资料，制作PPT或视频、文件材料，做好课上交流的准备.

教师活动：及时监督、指导学生活动的进度、内容、分工和辅导学生发言及研究工作.

设计意图：前面对三角函数的定义、图像和性质的学习是纯数学知识，三角函数来源于生活、服务于生活的理念学生并不知晓，为了调动学生的学习兴趣和学习积极性，让学生自己发现、挖掘、猜想和应用生活中的三角函数，大大提高了学生的参与度和学习兴趣，为数学建模做好铺垫.

（二）上课前一晚的教学活动

通过PAD给学生发自主学习任务单，学生独立完成，教师及时批阅.以下是自主学习任务单的具体内容：

1. 函数f（x）=Asin（ωx+φ）+B（A>0，ω>0）的图像与性质

（1）图像的画法：“五点法”和图像变换法.

（2）定义域：_______________.

（3）值域：________________，当x=_______________（k∈Z）时，f（x）取最大值A+B;当x=_______________（k∈Z）时，f（x）取最小值-A+B.

思考：如何用f（x）■和f（x）■求A和B的值？

（4）周期：T=_______________.

（5）奇偶性：当且仅当φ=kπ（k∈Z）时，函数f（x）=Asin（ωx+φ）是_________函数;当且仅当φ=kπ+■（k∈Z）时，函数f（x）=Asin（ωx+φ）是__________函数.

（6）单调性：单调递增区间是每一个____________;单调递减区间是每一个_________.

（7）对称性：函数图像与直线y=B的交点是对称中心，即对称中心是_________，对称轴与函数图像的交点的纵坐标是函数的最值，即对称轴是直线________.

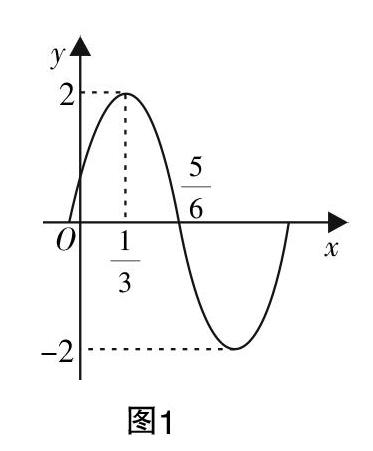
2. f（x）=Asin（ωx+φ）（x∈R，A>0，φ<■）的图像如图1所示.

（1）求f（x）的解析式;

（2）要得到y=sinx的图像，只需将f（x）的图像进行怎样的图像变换？

设计意图：复习并巩固函数f（x）=Asin（ωx+φ）+B（A>0，ω>0）的图像与性质，为本节课做好知识储备.

环节二：课堂教学设计

（一）复习反馈

对自主学习任务单的内容进行总结性讲评，学生的易错点是函数f（x）=Asin（ωx+φ）+B（A>0，ω>0）的对称中心是■，B（k∈Z），教师强调第2题图像变换的格式.

（二）新课引入

学生朗读白居易《琵琶行》片段并配有琵琶乐曲：“低眉信手续续弹，说尽心中无限事. 轻拢慢捻抹复挑，初为《霓裳》后《六幺》. 大弦嘈嘈如急雨，小弦切切如私语. 嘈嘈切切错杂弹，大珠小珠落玉盘. 间关莺语花底滑，幽咽泉流冰下难. 冰泉冷涩弦凝绝，凝绝不通声暂歇.别有幽愁暗恨生，此时无声胜有声……座中泣下谁最多？江州司马青衫湿.”学生深情地朗读完后，教师现场采访该学生，师说：“你能从这首诗里感受到数学的韵律吗？说得再贪婪些，这里有没有三角函数的味道？”生很严肃地答：“绝对有！琵琶旋律由舒缓到急促再到舒缓，音调由高到低再到高，在平面直角坐标系下描绘出的就是正弦型函数的图像.”由此引出本节课的课题《生活中的三角函数》.

设计意图：以诗的形式作为本节课的开篇之作，增强数学的人文素养，最出彩的是读诗后的师生对话，幽默而又切合主题，课堂气氛立刻被调动起来！

（三）开启《生活中的三角函数》之旅

第一组：经济团队的《爱心曲线》

学生活动：学生介绍了笛卡尔的生平简介和主要的思想成就、心形线背后凄美的爱情故事，由此引出极坐标系下的曲线和方程的关系，并让学生亲手绘制爱心曲线，巩固了极坐标系的相关内容.

教师点评：从凄美的爱情故事中我们引出了与平面直角坐标系不同的极坐标系，它在生活实际中应用非常广泛，而且通过爱心曲线，我们发现极坐标系与三角函数有着非常密切的联系. 对老师感触最深的是笛卡尔晚上睡不着，看到蜘蛛在棚顶织网，发明了直角坐标系，由此有了方程，然后所有的数学问题都可以归结为代数问题，用方程来解决.教师希望学生也要有这样的数学洞察力，把生活中的问题概括出数学模型，用数学知识得以解决.

设计意图：从凄美的爱情故事中让学生发现三角函数无处不在，极坐标系虽然还没学，但让学生利用所学知识自主探究完全可以胜任，从笛卡尔的发明创造开启了数学建模意识和思想，顺利地过渡到下一组的《声音与三角函数》模块.

第二组：数学微团2班的《声音与正弦》

学生活动：学生发现正弦函数图像与声音的传播形式声波以及产生的三要素高度一致，猜想物理中的声音与数学中的三角函数有高度的相关性，学生通过查找资料、在网上下载视频“声波形成的正弦曲线”，让学生高度感知到数理不分家，三角函数与物理中的简谐振动、声音的传播、交流电等都有非常密切的联系.

教师点评：这个团队的优点是发现案例后，学生敢大胆地猜想，并用实验和视频材料加以论证，最记忆犹新的是主持人告诉笔者他的猜想，过了几天后，他激动而又惊喜地告诉笔者，他找到了证明这个猜想的视频材料，随着声音要素的改变，手龙头下出来的水花形状就是正弦曲线！那孩子眼中的惊喜是笔者一辈子都不会忘记的，也更加坚定了笔者要把课堂还给学生，让学生做课堂的主人，学生的潜力无限，只有这样才能充分地施展他們的才华！

第三组：数学微团1班的《潮汐》

学生活动：生活在大海边的孩子非常有必要了解一下潮汐的概念，这其中也蕴含着三角函数. 数学微团1班的主持人为学生们介绍了潮汐的概念和现象，并用上述知识解决了船舶进港和出港时间的数学应用问题.

教师点评：本小组的最大优点是利用潮汐的规律解决了船舶进港和出港时间问题，由一组数据拟合出三角函数模型，利用所学的三角函数知识解决生活实际问题，这正是数学建模和数学应用的步骤方法，本节课的教学目标被凸显出来.

第四组：数学微团4班的《如何设计生活中的三角函数模型》

学生活动：本小组系统地概括了数学建模的方法和具体步骤，并以“关于日地之间距离的三角函数模型讨论”为具体事例加以说明，并让学生以“天安门广场国旗升降具体时间”为课题让学生进行数学建模，解决实际问题.

教师点评：作为展示的最后一组，不仅引出了数学建模的案例，还教会学生数学建模的方法和步骤、需要注意的问题，本节课达到了实施教学目标的高潮！

（四）课外延伸

1. 自出生之日起，人的情绪、体力、智力等心理、生理状况就呈周期变化. 根据心理学家的统计，人体节律分为体力节律、情绪节律和智力节律三种. 这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段. 以上三个节律周期的半数为临界日，这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日. 临界日的前半期为高潮期，后半期为低潮期. 生日前一天是起始位置（平衡位置），请根据自己的出生日期，绘制自己的体力、情绪和智力曲线，并总结自己在什么时候应当控制情绪，在什么时候应当鼓励自己;在什么时候应当加强锻炼，在什么时候应当保持体力？

设计意图：在人的生理和心理领域也存在着三角函数，此案例实用性强，很受学生喜欢.

2. 请撰写一篇有关《生活中的三角函数》数学小论文.

设计意图：从发现、猜想、思考、论证、写作出发，让学生经历数学建模的全部过程，培养学生的数学核心素养，让学生终身受益.

（五）以诗结尾，首尾呼应

生活是正弦曲线

有时波峰，有时波谷

波峰时别得意忘形

波谷时别灰心丧气

没有波谷就没有波峰

没有波峰亦没有波谷

有波谷没有波峰人生不完美

有波峰没有波谷人生不完整

善待他人，理解命运

得意时不以物喜，失意时不以己悲

喜忧相伴，岁月飘香

学生活动：学生朗读，意犹未尽，意味深长……

设计意图：在正弦曲线中感悟人生，教给学生做人的道理，更紧扣主题：生活中的三角函数！

环节三：教学反思

本节课首先凸显学生的主体意识.在教学活动中充分发挥学生的主体作用，让学生亲自寻找生活中的三角函数，通过各小组的交流学习让学生深刻体会生活即数学的教育理念.

首先，学生从知识的被动接受转变为主动的参与者和积极的探索者，教师尊重学生个性，一切教学活动都应针对不同学生提供多种选择，为不同水平的学生设置不同层次的问题，打破“一把尺子量天下的做法”. 其次，培养学生数学建模的思想和能力，为后续数学建模奠定基础. 数学建模是数学六大核心素养之一，如何在课堂上培养学生的数学建模能力，值得每一位教师反思.通过本课的学习，学生掌握了数学建模的方法和步骤，数学论文的撰写方法，提升了学生的应用意识和创新素养. 再者，营造开放、平等的课堂气氛. “开放”就是实行民主教学，给学生思考的余地和交流的机会，让他们真正参与进来. “平等”就是师生间平等、学生间平等，让每一位学生都能以积极的心态和舒畅的心情参与学习活动，使其个性得以张扬.教师可尝试“互换教学角色”的课堂模式，安排一定课时，让学生在课堂展示和讲解其课外成果，教师只需现场提问或点评升华. 这种形式的课堂将大大调动学生的参与积极性，增强学生的学习兴趣和学习乐趣. 最后，在数学课堂渗透人文气息，加强多学科融合，对学生进行数学哲理和价值观教育，让课堂真正地活起来，让学生热爱数学，这才是教育的真谛！

环节四：对互联网+教学下的数学建模课总结与反思

2014年青岛二中开始实施的互联网+教学改革大大提升了学生的自学能力、提高了课堂效率. 2017年随着新课程改革的深入进行，青岛二中数学组的老师们借助互联网和PAD教学模式，使数学建模课在常规课程、选修课程、竞赛课程三个层次由浅入深进行教学. 常规课程：由现实情境问题引入课题，在章节结束安排建模实践案例讲解和探究实践，旨在提升学生的数学应用意识;选修课程：开设数学建模选修课，供数学MT学生选修，介绍和讲解更多基于高中知识的建模案例，加深学生对数学建模环节与流程的理解，能自主发现问题并建模解决问题;竞赛课程：组织学生参与各类数学建模竞赛，提供数学建模论文写作指导和软件编程实践机会，能合作解决问题并形成规范的论文. 例如函数章节的放稳椅子问题，三角函数章节的气温预测问题，解三角形章节的高度测量问题，数列章节的体温、体重预测问题，存款、贷款问题，不等式章节的洗衣服问题，立体几何章节的3D设计问题等. 青岛二中给予学生有充分的自主发展空间，利用周二周三选修课时间将数学热情高、数学能力强的学生聚集到数学MT，团队内具备浓厚的数学学习氛围.数学MT的导师们给予数学建模课程教学充分支持，同时也聘请丰富而优质的校外教学资源，如中国海洋大学数学院和青岛大学数学院的老师们给予学生建模学习的指导，学生多次参与海大的建模课程观摩;学校建有数学建模实验室，给学生软件操作、合作交流提供便利条件，使得一些建模能力强兴趣高的学生脱颖而出，发展了特长，为未来的专业选择确立了方向. 近三年来有多支队伍获得登峰杯初赛、决赛一等奖，美国高中生数学建模比赛特等奖及特等奖入围奖，成功举办了三届全国山海杯数学建模大赛并获得特等奖、一等奖等好成绩;数学建模社获得2017年优秀社团荣誉称号.

未来之路还很长，为了学生的长远发展，在互联网+教学的助力下，数学建模课定会乘风破浪、继续远航！