切换系统及其同步控制

颜闽秀, 徐 辉

(沈阳化工大学 a. 信息工程学院, b. 辽宁省工业环境-资源协同控制与优化技术重点实验室, 辽宁 沈阳 110142)

自Lorenz系统[1]被提出后,混沌及其控制理论研究成为热点,在通信保密,图像视频加密,神经网络等领域都得到一定的应用[2-4].为提高混沌同步在保密通信中的安全性能,研究人员致力于复杂混沌系统的构建,因此切换系统构建成为一个新的研究方向[5-10].文献[11-12]将Lorenz系统中第三维的非线性项xy改为x2,进而构建出有2个子系统的切换混沌系统.文献[13]更改Lorenz系统中的非线性项,同时引入线性反馈项x或y来构成含有四子系统的切换系统.文献[14]将Chen系统中第三维的非线性项xy改为x2来构建出有2个子系统的切换混沌系统.文献[15]将系统中一个变量的立方项添加到第一个方程中,构成有2个子系统的切换系统.

不难发现,上述构建切换系统研究中,其核心是对变量进行替换.本文基于Liu系统构建,利用坐标变换和参数符号切换的方法构建多翼切换混沌系统.相较于上述文献,本文的方法并不改变原系统的变量,且拓展了系统的机翼数目,有利于进行同步控制.而在研究切换系统的同步控制问题时,文献[14-15]将自适应控制应用在切换混沌系统同步中,取得了良好的实验结果.但并没有考虑干扰因素,在实际应用中,不可避免地存在干扰.所以,本文针对干扰上下界未知和参数不确定的切换系统同步控制问题进行进一步研究,设计出基于指数干扰观测的自适应控制器,实现了其同步控制且无须不确定性和干扰的上下界.

1 Liu系统坐标变换

Liu混沌系统模型为

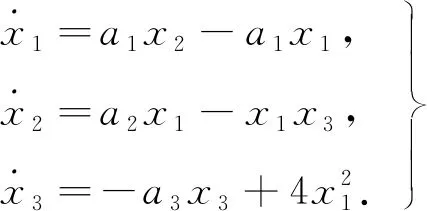
(1)

实数a1,a2,a3在一定范围内,式(1)会产生混沌吸引子,这里取a1=10,a2=15,a3=5.对式(1)作(x1,x2,x3)→(x1,x2,-x3)变换,得到式(2).

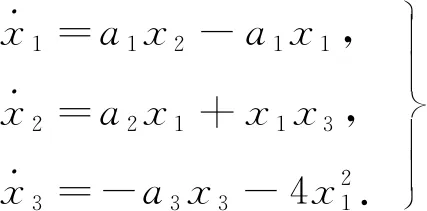
(2)

令(1,1,1)为式(1)的初始值,(1,1,-1)为式(2)的初始值,绘制它们的吸引子,如图1所示(见封3).

从图1中可以很直观地判断出式(2)是混沌的.下面,将进行参数切换,使得式(1)和式(2)成为四翼的切换混沌系统.

2 四翼切换Liu混沌系统

基于上述分析,提出四翼切换Liu混沌系统模型为

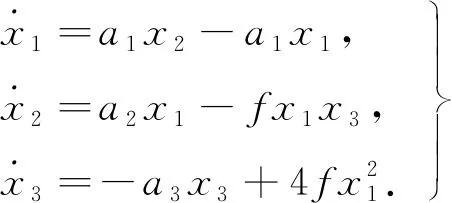
(3)

其中f为参数的切换函数,用于实现式(1)与式(2)的切换,其表达式如下:

f=sgn(sin(ρt)).

(4)

式中,ρ≠0为一常数,影响参数切换的周期.这里取ρ=0.05,则正弦函数的周期T=2π/ρ.在第1个T/2内f=1,式(3)以式(1)的模型运行.在第2个T/2内f=-1,式(3)以式(2)的模型运行.如此循环.

为便于分析系统的切换过程,设置仿真时间为t=1+T.取(1,1,1)为式(3)的初始值,绘制其吸引子相图,如图2所示(见封3).

图2中,图例数字1代表第1个T/2,数字2代表第2个T/2以及下一阶段的前1 s.由相图不难看出,式(3)是混沌的,其吸引子具有4翼,其运行模态为式(1)→(2)→(1).

为进一步验证式(3)的混沌特性,使用MATLAB运算得到系统的李雅普诺夫指数为:λL1=0.862,λL2=0,λL3=-15.835,进而计算出李雅普诺夫维数DL.

DL=2+(λL1+λL2)/λL3=2.054.

(5)

因λL1为正数,DL为分数,所以可准确判断出切换式(3)是混沌的.

3 切换混沌系统的电路仿真

设计式(3)的混沌电路如图3所示.

图3中,x=x1,y=x2,z=x3,运算放大器为LM324,模拟乘法器的增益为0.1,脉冲电压源F用来实现系统参数切换.

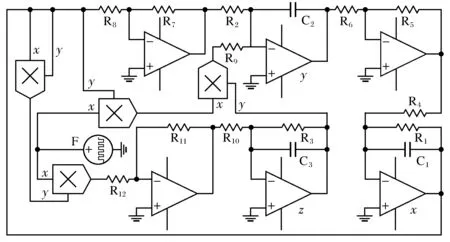
图3 切换Liu系统混沌电路Fig.3 Chaotic circuit of switching Liu system

由电路理论可得式(3)的实现方程为

(6)

切换函数f由脉冲电压源实现,脉冲电压源F内部参数设置如表1所示.

表1 脉冲电压源参量Table 1 Parameters of pulse voltage source

将式(6)与式(3)比较,对电容和电阻可作如下取值:

(7)

基于上述数据进行电路仿真实验,实验结果如图4所示.

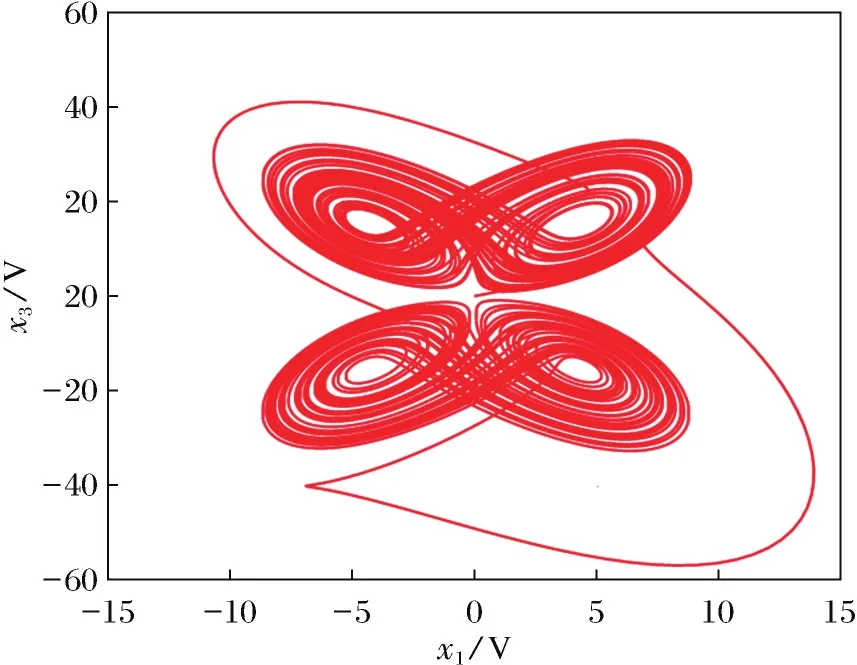
图4 吸引子平面图Fig.4 Plane phase diagram of attractor

从图4中可以看出,电路仿真结果与上文数值仿真的结果基本一致,这验证了切换系统实现的可能性.

4 切换系统的同步控制

4.1 理论分析

取式(3)作为驱动系统,并取如下响应系统:

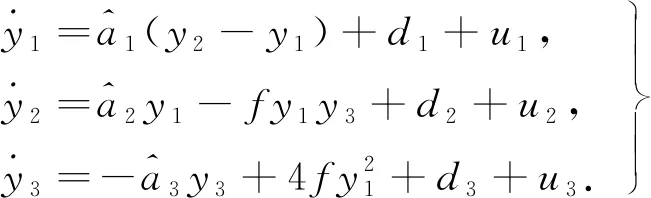
(8)

(9)

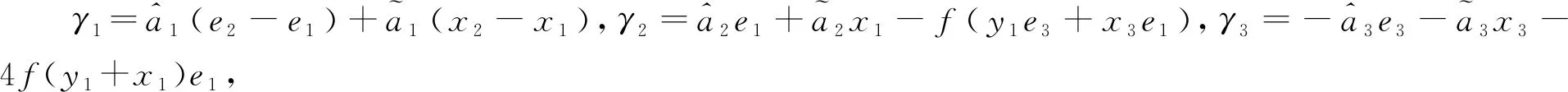
针对参数不确定和干扰上下界未知的混沌系统,为实现其同步控制,将首先设计指数干扰观测器,实现对干扰的补偿,加快系统的同步响应速度.观测器设计的基本思想是用估计输出与实际输出的差值对估计值进行修正,因此设计辅助指数干扰观测器为

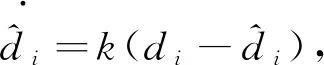
(10)

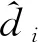
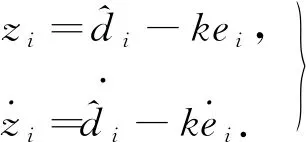
(11)

将式(9)代入式(10)可以得到

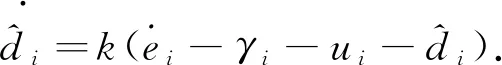
(12)

将式(12)代入式(11),得到指数干扰观测器为

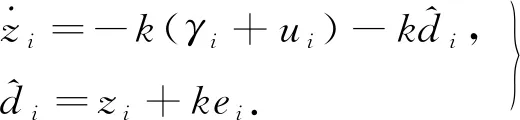
(13)

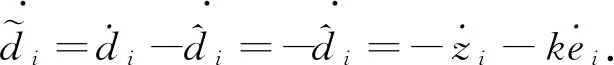
(14)

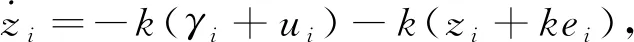
(15)

将式(15)代入式(14),则

由式(16)可得到观测误差方程并求其解,则

(17)

可见通过取适当的k值,可使观测误差按指数速率逼近于0.针对不确定参数,设计其自适应律为

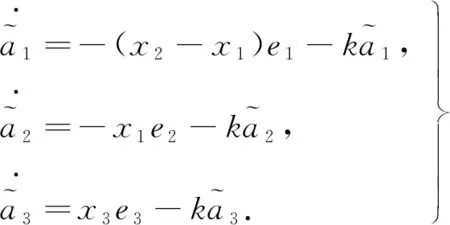
(18)

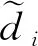
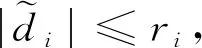
(19)

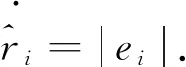
(20)

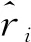
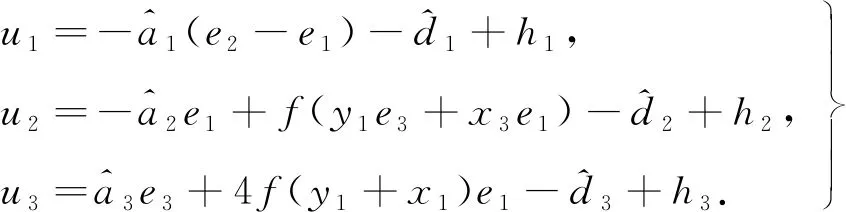
(21)

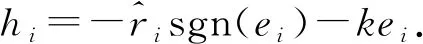
定理1 在观测器式(13)、自适应律式(18)和式(20)、及控制器式(21)的作用下,响应系统式(8)将与驱动系统式(3)实现同步.

证明1 构造如下李雅普诺夫函数

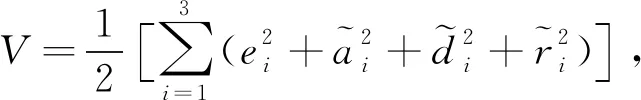
(22)

对式(22)求导,则

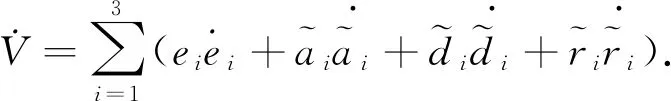
(23)

将式(9)代入式(23),有

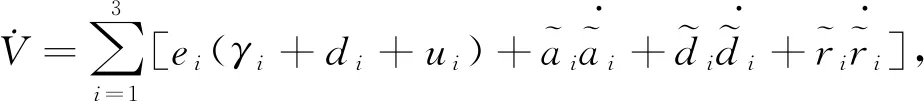
(24)

将式(18),式(21)代入式(24)计算并化简,则有

将式(16),式(20)代入式(25),计算得

因为k>0,那么对式(26)进行放缩计算,则有

因为ei≤|ei|,将式(19)代入式(27)进行放缩计算,则有

综上,定理1证毕.

4.2 数值仿真

综上所述,文中设计的基于干扰观测的自适应控制器能够实现切换混沌系统的同步控制且无须不确定参数和外加干扰的上下界,具有有效性和可行性.

5 结 论

本文提出了坐标变换后切换参数符号的方法来构建多翼切换混沌系统,并成功构建出四翼的切换Liu系统,通过动力学特性研究验证了其混沌特性.针对不确定参数和未知上下界干扰的混沌系统同步控制问题,设计了基于指数干扰观测器的自适应同步控制器,实现了四翼切换混沌系统的同步控制.该构造方法和同步控制方法在通信保密领域具有潜在的应用性.