概率2-度量空间中Φ-压缩映象对的公共不动点
张树义, 聂 辉
(渤海大学 数理学院, 辽宁 锦州 121013)
关于概率度量空间和模糊度量空间概念及在此空间中建立的不动点定理,文献[1-12]做过研究,其中文献[3]使用控制函数在G-完备Menger概率度量空间研究了一类映象的不动点的存在性.文献[4-6]在非阿基米德概率2-度量空间中建立了几类映象不动点定理,文献[7]在非阿基米德概率度量空间中建立了Altman型映象的公共不动点定理,文献[8-9]在模糊度量空间中利用模糊度量M满足三角不等式的概念建立了一类压缩映象公共不动点定理.文献[10-12]在模糊度量空间中利用模糊度量M满足三角不等式的概念建立了一类积分型以及Φ-压缩型映象的不动点定理推广了文献[8-9]中的结果.近年来,文献[13-15]研究了几类非线性映象不动点的存在性与迭代逼近.受上述工作启发,本文在一定条件下,在Menger概率2-度量空间中建立一类Φ-压缩映象对新的公共不动点的存在性定理.
1 预备知识
下面回忆一些基本概念, 其中定义1~4可在文献[1-7]查到.
定义1 映象f:=(-∞,+∞)→+=[0,+∞)称为分布函数,如果它是不减的,左连续的,
定义2 映象Δ:[0,1]×[0,1]×[0,1]→[0,1]称为三角范数(简称t-范数),如果满足以下条件
ⅰ) ∀a∈[0,1],Δ(a,a,1)=a;
ⅱ) ∀a,b,c∈[0,1],Δ(a,b,c)=
Δ(a,c,b)=Δ(c,a,b);
ⅲ) ∀a,b,c,d,e,f∈[0,1],若a≥d,b≥e,
c≥f,有Δ(a,b,c)≥Δ(d,e,f);
ⅳ) ∀a,b,c,d,e∈[0,1],Δ(Δ(a,b,c),d,e)=Δ(a,Δ(b,c,d),e)=Δ(a,b,Δ(c,d,e)).
定义3 (X,F,Δ) 称为Menger概率2-度量空间,如果X是非空集,Δ是t-范数,D为全体分布函数,F:X×X×X→D,记分布函数F(x,y,z)为Fx,y,z,而Fx,y,z(t)表示Fx,y,z在t∈的值.若满足下面条件:
ⅰ)Fx,y,z(0)=0,∀x,y,z∈X;
ⅱ) 对∀x,y∈X,存在z∈X,t0>0,使得
0≤Fx,y,z(t0)<1;
ⅲ)Fx,y,z(t)=1,∀t>0,则x,y,z至少有2个相等;
ⅳ)Fx,y,z=Fx,z,y=Fy,z,x,∀x,y,z∈X;
ⅴ) 若∀x,y,z,w∈X,∀t1,t2,t3∈
[0,+∞),有
定义4 设(X,F,Δ)是Menger概率2-度量空间,序列{xn}⊂X. 如果对∀ε>0,λ>0,a∈X,存在N(ε,λ,a)∈(正整数集),使得∀n≥N,有Fxn,x,a(ε)>1-λ,则称{xn}收敛到点x∈X.如果对∀ε>0,λ>0,a∈X,存在N(ε,λ,a)∈,使得对∀n,m≥N,有Fxn,xm,a(ε)>1-λ,则称{xn}为Cauchy序列.如果X中的每个Cauchy序列都收敛,则称(X,F,Δ)是完备的.
定义5 Menger概率2-度量空间(X,F,Δ)中的序列{xn}称为G- Cauchy序列,如果对每一个p∈,如果X中的每个G- Cauchy序列都是收敛的,则称为Menger概率2-度量空间(X,F,Δ)是G- 完备的.
设Ω={g|g:[0,1]→[0,∞)连续,严格递减,g(1)=0,g(0)=+∞}.
定义6[6]Menger概率2-度量空间(X,F,Δ)称为(C)g型的,如果存在g∈Ω,使得∀x,y,z,w∈X,∀t≥0,有gFx,y,z(t)≤gFx,y,w(t)+gFx,w,z(t)+gFw,y,z(t).
定义7 设(X,F,Δ)是概率2-度量空间,概率2-度量F称为三角的,如果∀x,y,z,w∈X, ∀t>0,有
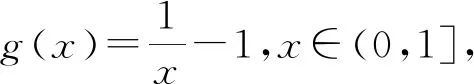
Φ1={Φ|Φ:[0,+∞)→[0,+∞),Φ(0)=0}.
由文献[6]易知下面引理1成立.
引理1[6]设(X,F,Δ)是(C)g型的概率2-度量空间,{xn}⊂X,∀t>0,如果∀a∈X,有
则对∀n,m≥1,有Fxn,xn+1,xm(t)=1,其中Φ∈Φ1,0 以下设t-范数Δ是连续的. 定理1 设(X,F,Δ)是(C)g型的G- 完备Menger概率2-度量空间,f与h是X上的自映象,满足下列不等式组: 其中,φ:+=[0,+∞)→+是勒贝格可积与可和的,且φ(t)dt>0,ε>0.Φ∈Φ1,∀x∈X,t>0,0 证明 对x0∈X, 可归纳定义序列{xn}为x2n+1=fx2n,x2n+2=hx2n+1,n=0,1,2…,如果对某个n,xn=xn+1, 则易知xn是f与h在X上一公共不动点.以下假设对任意n≥0,xn≠xn+1, 由式(2),对∀t>0,∀a∈X,有 类似,由式(1) ∀t>0,∀a∈X,可得 由式(3)和式(4),∀t>0,∀a∈X,有 于是n≥0,t>0,∀a∈X,有 从而 连续n次使用上面不等式有 由式(5),∀t>0,∀a∈X, 有 于是对∀t>0,∀a∈X,有Fxn+1,xn+2,a(t)→1(n→∞).据定义3,∀t>0,∀a∈X,有 由引理1,并在式(6)中令n→∞,对任意p∈,∀t>0,∀a∈X,有Fxn,xn+p,a(ε)→1(n→∞).因此{xn}是一G- Cauchy序列. 由于(X,F,Δ)是G- 完备的,于是存在z∈X,使由f的连续性,因此z是f不动点.由式(2)∀t>0,∀a∈X,有 从而∀t>0,∀a∈X,有gFhz,z,a(t)=0,于是hz=z.故z是f与h在X上一公共不动点.类似,h连续性,f与h在X上有一公共不动点.证毕. 注2 定理1中附加 ⅰ) 取Φ(t)=λt(0<λ≤1),0 ⅱ)Φ(t)=λt(0<λ<1),0 在定理1令f=h,C=max{A,B},则有 推论1 设(X,F,Δ)是G- 完备Menger概率度量空间,f是X上的自映象满足下列不等式 其中,φ:+=[0,+∞)→+是勒贝格可积且φ(t)dt>0,ε>0.∀x∈X,t>0,0 如果f连续,则f在X上有一不动点. 注3 在定理1中若用完备的Menger概率度量空间代替G- 完备的Menger概率度量空间,而连续t-范数取为Δ(α,β)=min{α,β},α,β∈[0,1],则容易证明定理1也成立. 由注1和定理1可得如下结果. 定理2 设(X,F,Δ)是具有F三角的G- 完备Menger概率2-度量空间,f与g是X上的自映象,满足下列不等式组: 其中,φ:+=[0,+∞)→+是勒贝格可积与可和的,且φ(t)dt>0,ε>0.∀x∈X,t>0,0 如果f或h连续,则f与h在X上有一公共不动点. 随着不动点理论的发展, 提出新的不动点存在性定理借以统一以往的研究成果, 是不动点理论发展趋势之一. 本文在Menger概率2-度量空间框架下, 利用控制函数建立一类积分型Φ-压缩映象对新的公共不动点的存在性定理, 最终将相关文献中的结果推广到了积分型Φ-压缩映象对的情形, 扩展了其不动点定理的适用范围.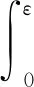
2 主要结果
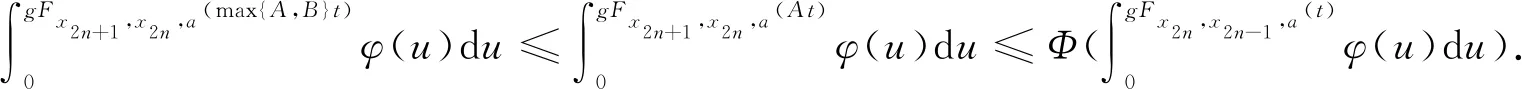
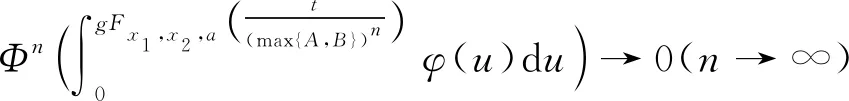
3 结 论

