幂函数问题变式探究
◇ 湖北 冯 赟
在高中数学中,对幂函数的学习要求并不高,我们只需掌握它解析式的求法、图象与性质的基本应用即可.本文从一个例题进行推广与探究.
1 引例探究
引例已知函数f(x)=(m2-m-1)x-5m-3,求m 的取值,使得
(1)f(x)是幂函数;
(2)f(x)是幂函数,且是(0,+∞)上的增函数.
分析(1)抓住幂函数的定义:形如y=xα(α 是常数)的函数是幂函数.
(2)抓住幂函数的性质:当指数α>0时,幂函数y=xα(α 是常数)是(0,+∞)上的增函数.
解(1)因为f(x)是幂函数,故m2-m-1=1,即m2-m-2=0,解得m=2或-1.
(2)若f(x)是幂函数,且又是(0,+∞)上的增函数,则所以m=-1.
研究幂函数应从解析式入手,再考查它的图象特征,即抓住幂函数的基本性质.
2 变式训练
变式1幂函数y=f(x)的图象过点(4,2),则幂函数y=f(x)的图象是( ).

设幂函数的解析式为f(x)=xα,则4α=2,解得所以故选C.
变式2当0<x<1 时,f(x)=x1.1,g(x)=x0.9,h(x)=x-2的大小关系是.
图1为函数f(x),g(x),h(x)的图象,由此可知0<x<1时,h(x)>g(x)>f(x).
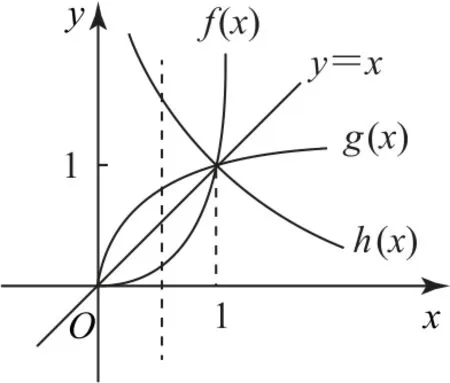
图1
当幂函数的底数相同时,幂函数的大小比较问题,往往可采用图象法求解.
变式3已知幂函数f(x)=xα的部分对应值如表1,则不等式f(|x|)≤2的解集是( ).

表1
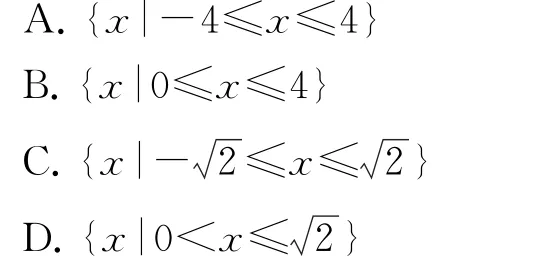
变式4已知幂函数经过点试确定m 的值,并求满足条件f(2-a)>f(a-1)的实数a 的取值范围.
本题通过解不等式f(2-a)>f(a-1)求参数a,依然利用了幂函数的单调性,但有个易错点容易被忽视,即忽视函数的定义域,遗漏2-a≥0和a-1≥0这两个条件.
总之,解幂函数问题必须关注幂函数的定义、图象与性质.由于幂函数y=xα中常数α 的变化,函数图象也有变化,一般只关注第一象限的图象,由α 的正负确定它的单调性和图象,由常数α 的特征来确定函数的定义域和奇偶性.因此研究幂函数归根结底是研究指数α 的变化与函数图象之间的变化.既要抓住图象的共同特征,即都过点(1,1),又要关注常数α 的特性.我们需特别关注以下几点:
1)形如y=xα(α 为常数)才是幂函数,而函数f(x)=3x5不是幂函数;
2)画幂函数图象必须先关注定义域,幂函数的定义域不都是实数集R,它还可能是正数集,如f(x)=还可能是正数集与负数集的并集,如f(x)=x-2,幂函数不一定都具有奇偶性;
3)幂函数的单调性主要用于比较数值大小与解相关不等式,解题时需注意数形结合;
4)幂函数的图象在第一象限一定出现,而第四象限一定没有.

图2
链接练习
1.图2 是函数y=xm/n(m,n∈N*,m,n 互质)的图象,则( ).
2.y=(x-1)α+1(α>0)的图象恒过定点.
3.若函数f(x)是幂函数,且满足f(4)=3f(2),则)的值等于.
4.若函数f(x)=(m2-m-1)是幂函数,且在(0,+∞)上是减函数,则实数m=.
链接练习参考答案

