特殊的题型,特殊的解法
◇ 山东 张 辉
处理有关线性规划问题时,常常会遇到一些特殊的题型,正是因为题型的特殊性,自然也会出现一些特殊的解法.本文通过归类解析,帮助同学们拓宽解题思维和视野,提升解题技能.
1 借助“分解因式”变形,巧画不等式组表示的平面区域
例1已知函数f(x)=x2-5x+4,则不等式组表示的平面区域为( ).

因为f(x)=x2-5x +4,所以f(x)-f(y)=x2-5x-y2+5y=(x-y)(x+y)-5(x-y)=(x-y)(x +y-5),所 以 不 等 式 组故其对应的平面区域应为图C.
通过对f(x)-f(y)的分解变形,有利于将不熟悉的问题转化为熟悉的问题.
2 借助“换元”变形,巧求动点表示的平面区域的面积
例2若变量x,y 满足则点P(2x-y,x+y)表示平面区域的面积是( ).
A.1 B.2 C.3 D.4
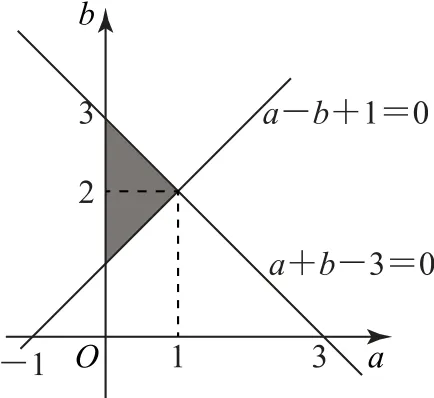
图1
本题先借助换元变形得到动点横坐标与纵坐标满足的不等式组,再画出该不等式组表示的平面区域,最后求面积即可.
3 借助“解方程组思想”,巧解给定目标函数的最值问题
例3已 知x,y 满 足且目标函数z=2x+y 的最大值为7,最小值为1,则为( ).
A.2 B.1 C.-1 D.-2

图2
本题的设计比较新颖,求解的关键在于灵活运用解方程组的思想求出目标函数的两个最优解.
4 借助“平面几何”分析,巧求参数的最值
例4已知s 是正实数,若不等式组表示的区域内存在一个半径为1的圆,则s 的最小值为( ).

画出不等式组所表示的平面区域,如图3所示.当s 最小时,已知不等式组所表示的区域为第一象限的一个等腰直角三角形区域,且半径为1 的圆与各边界相切.
设三角形直角边边长为a+1,则由直线与圆相切可知斜边长为2a,所以(a+1)2+(a+1)2=(2a)2,解得,从而,smin=,故选C.
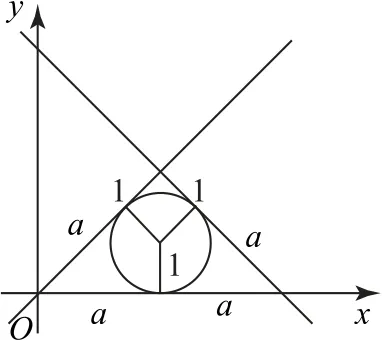
图3
本题先借助s 的几何意义分析何时s 会取得最小值,然后再借助平面几何知识分析此时的图形特点,最后进行运算即可.
综上,求解有关线性规划问题时,需要灵活运用所学数学知识与方法,以便将不熟悉的数学问题等价转化为熟悉的数学问题.同时还要注意“数形结合思想”在解题中的运用,有利于强化“数”与“形”之间的互化意识,进一步培养直观想象、数学运算等核心素养.一言以蔽之,且学且悟且提升.

