“七法”巧解双变元最值题
2020-08-17 05:37吉林于兴君
高中数理化 2020年12期
◇ 吉林 于兴君
在高中数学中,函数或代数式的最值问题是各类考试中比较常见的题型,也是高考中的重要考点.此类问题难度不小,但破解方法较多,常见的方法有基本不等式法、待定系数法、导数法、换元法、柯西不等式法等.本文结合一道二元代数式的最值问题来加以实例剖析,结合多维视角切入.
题目已知正数a,b 满足a+b=1,则的最大值为.
角度1基本不等式法
解法1由于正数a,b 满足a+b=1,所以
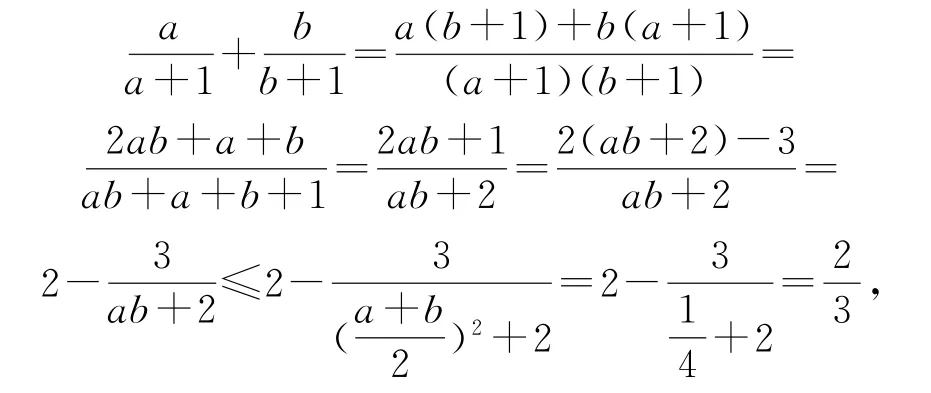
角度2二次函数的图象与性质法
解法2由于正数a,b 满足a+b=1,则有a=1-b(0<b<1),那么0<b<1,结合二次函数的图象与性质可知fmax(b)=此时
角度3换元法
解法3由于正数a,b 满足a+b=1,可设a=所以
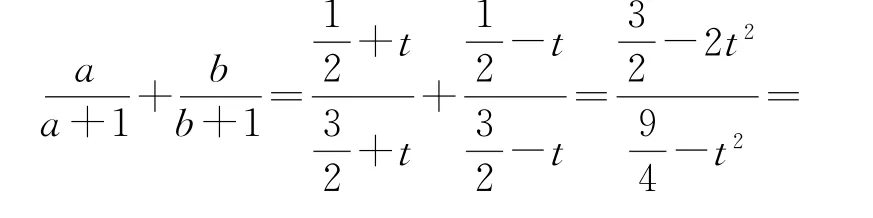

角度4柯西不等式法
解法4由于正数a,b 满足a+b=1,所以

角度5因式分解法
解法5由于当x 为正数时,(2x-1)2≥0,则4x2-4x+1≥0,即4x2+5x+1≥9x,(x+1)(4x+1)≥9x,故,当且仅当时,等号成立,所以当且仅当时,等号成立.
角度6三角换元法
解法6由于正数a,b 满足a+b=1,设a=所以
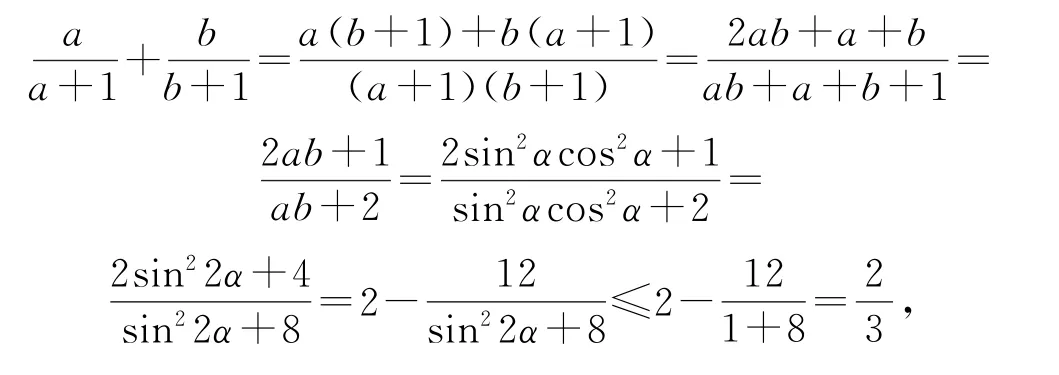
当且仅当sin22α=1,即时,等号成立.
角度7导数法
解法7由于正数a,b 满足a+b=1,则a=1-b(0<b<1),那么则令f′(b)=0,即解 得所以fmax(b)=此时
猜你喜欢
中学数学研究(广东)(2022年13期)2022-08-29
河北理科教学研究(2020年3期)2021-01-04
高师理科学刊(2020年2期)2020-11-26
语数外学习·高中版中旬(2020年2期)2020-09-10
河北理科教学研究(2020年1期)2020-07-24
重型机械(2019年3期)2019-08-27
高中生学习·高三版(2017年6期)2017-06-12
数学学习与研究(2016年18期)2017-01-07
初中生世界·七年级(2016年10期)2016-11-07
初中生世界·七年级(2016年10期)2016-11-07

